AttriReBoost: A Gradient-Free Propagation Optimization Method for Cold Start Mitigation in Attribute Missing Graphs

Missing attribute issues are prevalent in the graph learning, leading to biased outcomes in Graph Neural Networks (GNNs). Existing methods that rely on feature propagation are prone to cold start problem, particularly when dealing with attribute resetting and low-degree nodes, which hinder effective propagation and convergence. To address these challenges, we propose AttriReBoost (ARB), a novel method that incorporates propagation-based method to mitigate cold start problems in attribute-missing graphs. ARB enhances global feature propagation by redefining initial boundary conditions and strategically integrating virtual edges, thereby improving node connectivity and ensuring more stable and efficient convergence. This method facilitates gradient-free attribute reconstruction with lower computational overhead. The proposed method is theoretically grounded, with its convergence rigorously established. Extensive experiments on several real-world benchmark datasets demonstrate the effectiveness of ARB, achieving an average accuracy improvement of 5.11% over state-of-the-art methods. Additionally, ARB exhibits remarkable computational efficiency, processing a large-scale graph with 2.49 million nodes in just 16 seconds on a single GPU. Our code is available at https://github.com/limengran98/ARB.

Network Clustering Via Kernel-ARMA Modeling and the Grassmannian The Brain-Network Case

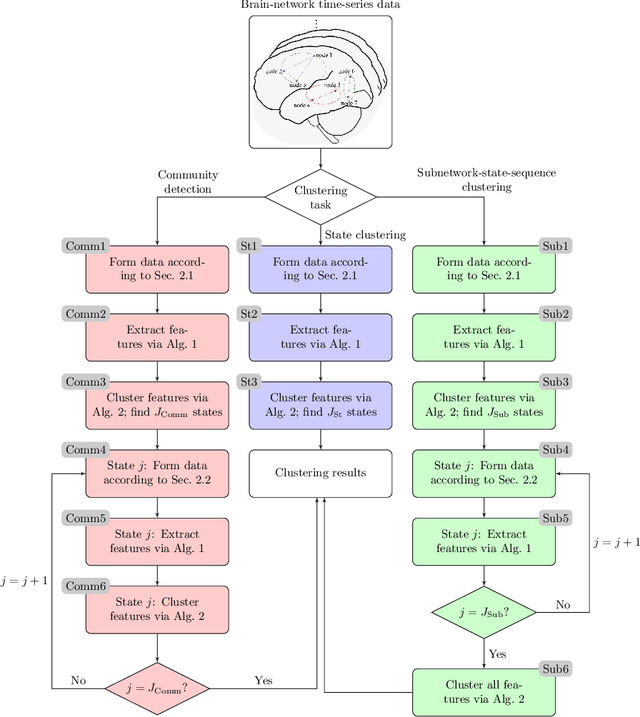
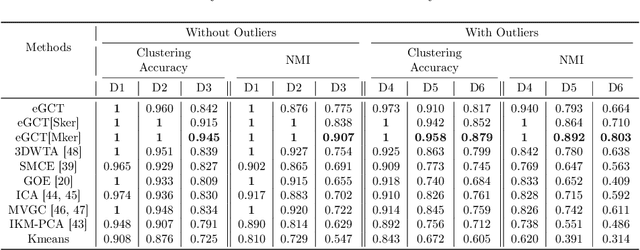
This paper introduces a clustering framework for networks with nodes annotated with time-series data. The framework addresses all types of network-clustering problems: State clustering, node clustering within states (a.k.a. topology identification or community detection), and even subnetwork-state-sequence identification/tracking. Via a bottom-up approach, features are first extracted from the raw nodal time-series data by kernel autoregressive-moving-average modeling to reveal non-linear dependencies and low-rank representations, and then mapped onto the Grassmann manifold (Grassmannian). All clustering tasks are performed by leveraging the underlying Riemannian geometry of the Grassmannian in a novel way. To validate the proposed framework, brain-network clustering is considered, where extensive numerical tests on synthetic and real functional magnetic resonance imaging (fMRI) data demonstrate that the advocated learning framework compares favorably versus several state-of-the-art clustering schemes.

Brain-Network Clustering via Kernel-ARMA Modeling and the Grassmannian

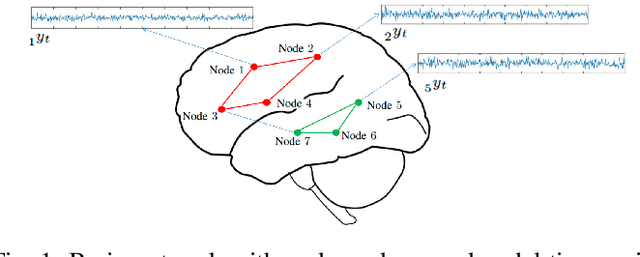
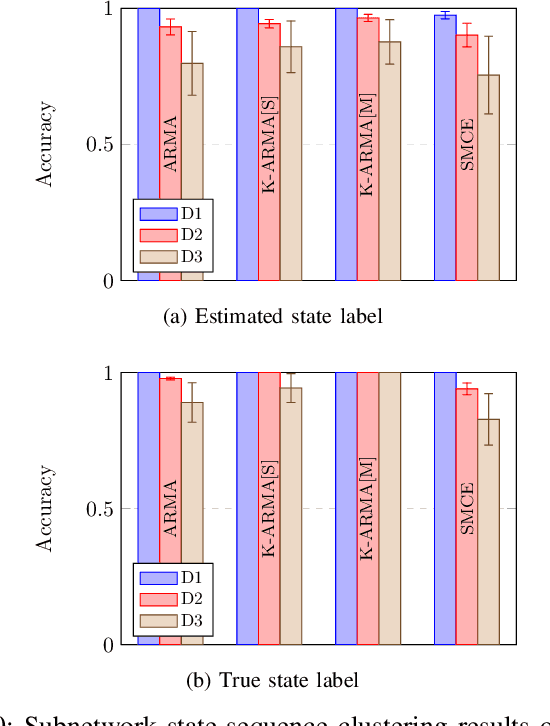
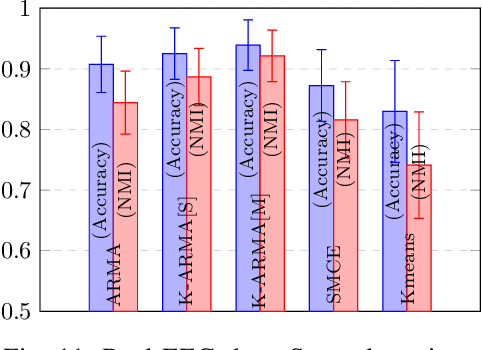
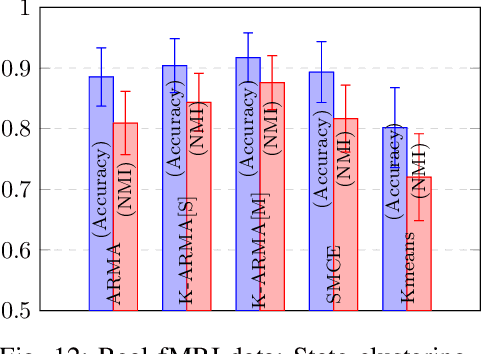
Recent advances in neuroscience and in the technology of functional magnetic resonance imaging (fMRI) and electro-encephalography (EEG) have propelled a growing interest in brain-network clustering via time-series analysis. Notwithstanding, most of the brain-network clustering methods revolve around state clustering and/or node clustering (a.k.a. community detection or topology inference) within states. This work answers first the need of capturing non-linear nodal dependencies by bringing forth a novel feature-extraction mechanism via kernel autoregressive-moving-average modeling. The extracted features are mapped to the Grassmann manifold (Grassmannian), which consists of all linear subspaces of a fixed rank. By virtue of the Riemannian geometry of the Grassmannian, a unifying clustering framework is offered to tackle all possible clustering problems in a network: Cluster multiple states, detect communities within states, and even identify/track subnetwork state sequences. The effectiveness of the proposed approach is underlined by extensive numerical tests on synthetic and real fMRI/EEG data which demonstrate that the advocated learning method compares favorably versus several state-of-the-art clustering schemes.