Pratik V. Patil
Network Clustering Via Kernel-ARMA Modeling and the Grassmannian The Brain-Network Case
Feb 18, 2020

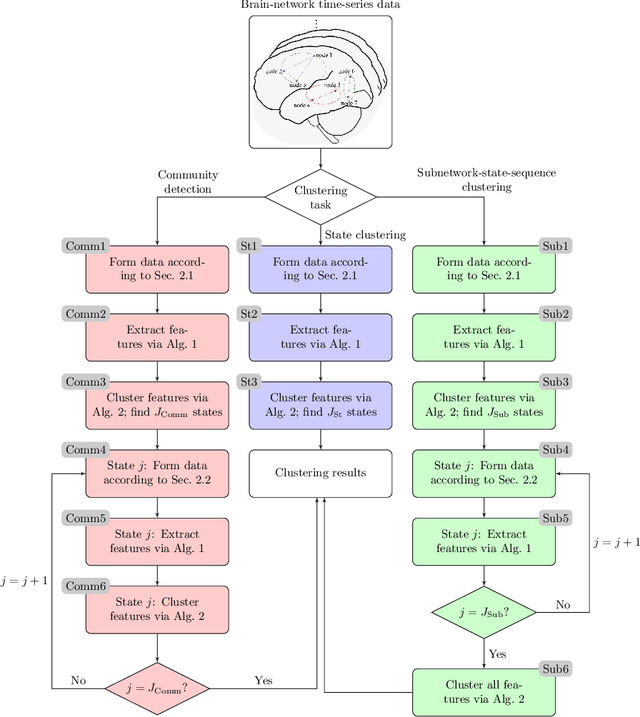
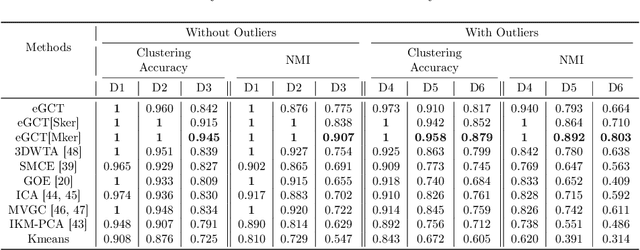
Abstract:This paper introduces a clustering framework for networks with nodes annotated with time-series data. The framework addresses all types of network-clustering problems: State clustering, node clustering within states (a.k.a. topology identification or community detection), and even subnetwork-state-sequence identification/tracking. Via a bottom-up approach, features are first extracted from the raw nodal time-series data by kernel autoregressive-moving-average modeling to reveal non-linear dependencies and low-rank representations, and then mapped onto the Grassmann manifold (Grassmannian). All clustering tasks are performed by leveraging the underlying Riemannian geometry of the Grassmannian in a novel way. To validate the proposed framework, brain-network clustering is considered, where extensive numerical tests on synthetic and real functional magnetic resonance imaging (fMRI) data demonstrate that the advocated learning framework compares favorably versus several state-of-the-art clustering schemes.
Brain-Network Clustering via Kernel-ARMA Modeling and the Grassmannian
Jun 05, 2019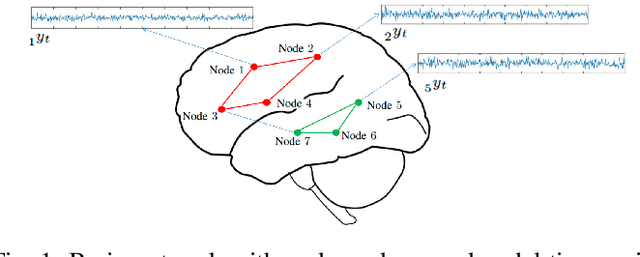
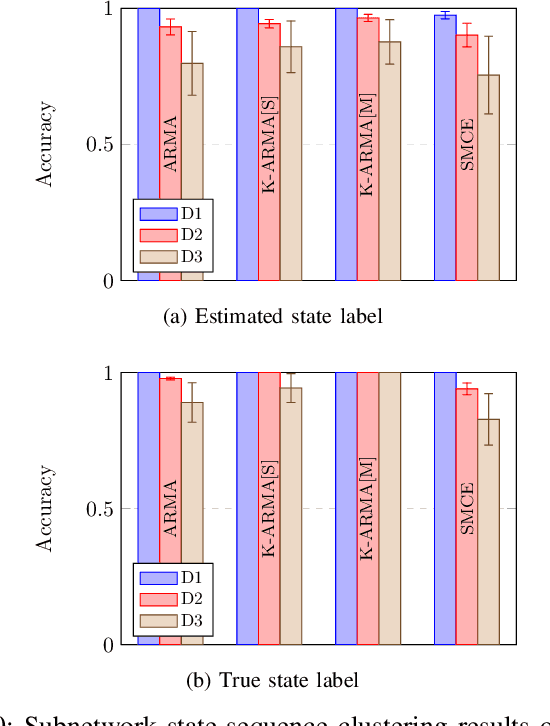
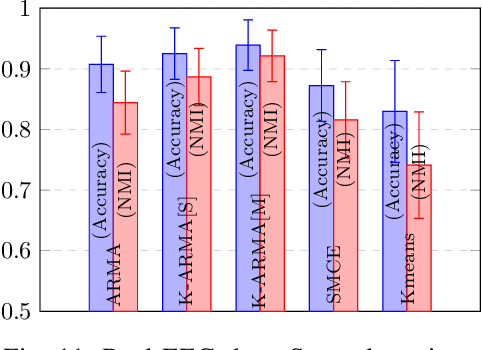
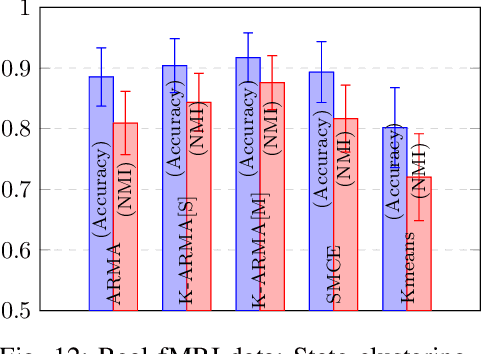
Abstract:Recent advances in neuroscience and in the technology of functional magnetic resonance imaging (fMRI) and electro-encephalography (EEG) have propelled a growing interest in brain-network clustering via time-series analysis. Notwithstanding, most of the brain-network clustering methods revolve around state clustering and/or node clustering (a.k.a. community detection or topology inference) within states. This work answers first the need of capturing non-linear nodal dependencies by bringing forth a novel feature-extraction mechanism via kernel autoregressive-moving-average modeling. The extracted features are mapped to the Grassmann manifold (Grassmannian), which consists of all linear subspaces of a fixed rank. By virtue of the Riemannian geometry of the Grassmannian, a unifying clustering framework is offered to tackle all possible clustering problems in a network: Cluster multiple states, detect communities within states, and even identify/track subnetwork state sequences. The effectiveness of the proposed approach is underlined by extensive numerical tests on synthetic and real fMRI/EEG data which demonstrate that the advocated learning method compares favorably versus several state-of-the-art clustering schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge