A Bayesian Bradley-Terry model to compare multiple ML algorithms on multiple data sets

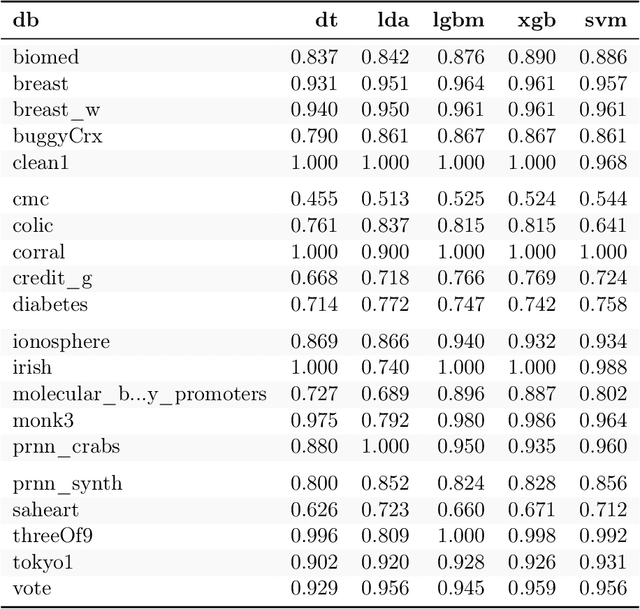
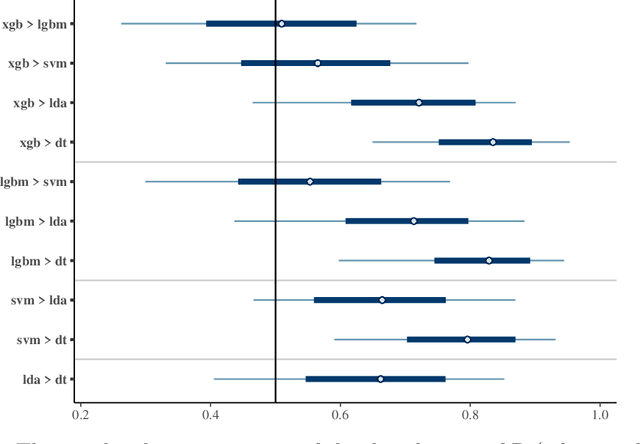
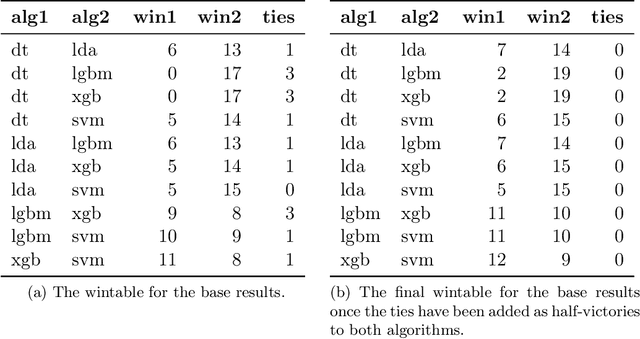
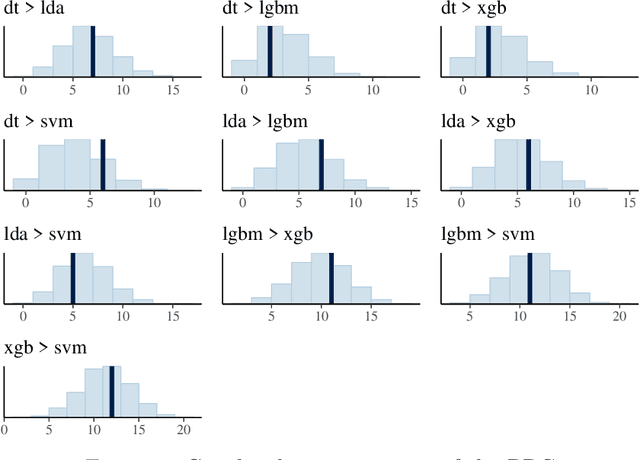
This paper proposes a Bayesian model to compare multiple algorithms on multiple data sets, on any metric. The model is based on the Bradley-Terry model, that counts the number of times one algorithm performs better than another on different data sets. Because of its Bayesian foundations, the Bayesian Bradley Terry model (BBT) has different characteristics than frequentist approaches to comparing multiple algorithms on multiple data sets, such as Demsar (2006) tests on mean rank, and Benavoli et al. (2016) multiple pairwise Wilcoxon tests with p-adjustment procedures. In particular, a Bayesian approach allows for more nuanced statements regarding the algorithms beyond claiming that the difference is or it is not statistically significant. Bayesian approaches also allow to define when two algorithms are equivalent for practical purposes, or the region of practical equivalence (ROPE). Different than a Bayesian signed rank comparison procedure proposed by Benavoli et al. (2017), our approach can define a ROPE for any metric, since it is based on probability statements, and not on differences of that metric. This paper also proposes a local ROPE concept, that evaluates whether a positive difference between a mean measure across some cross validation to the mean of some other algorithms is should be really seen as the first algorithm being better than the second, based on effect sizes. This local ROPE proposal is independent of a Bayesian use, and can be used in frequentist approaches based on ranks. A R package and a Python program that implements the BBT is available.

How to tune the RBF SVM hyperparameters?: An empirical evaluation of 18 search algorithms

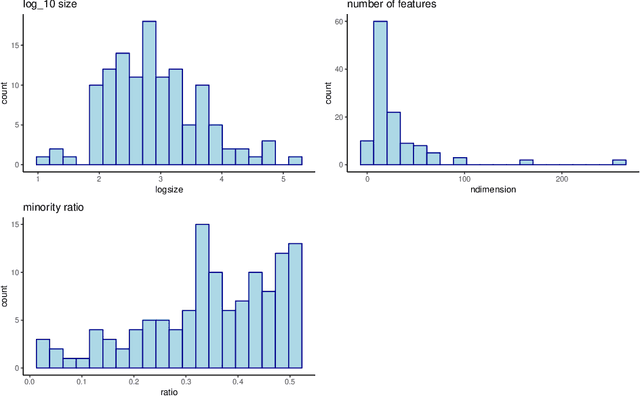
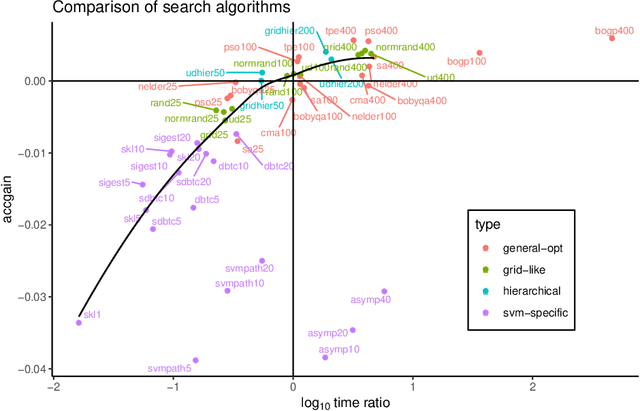
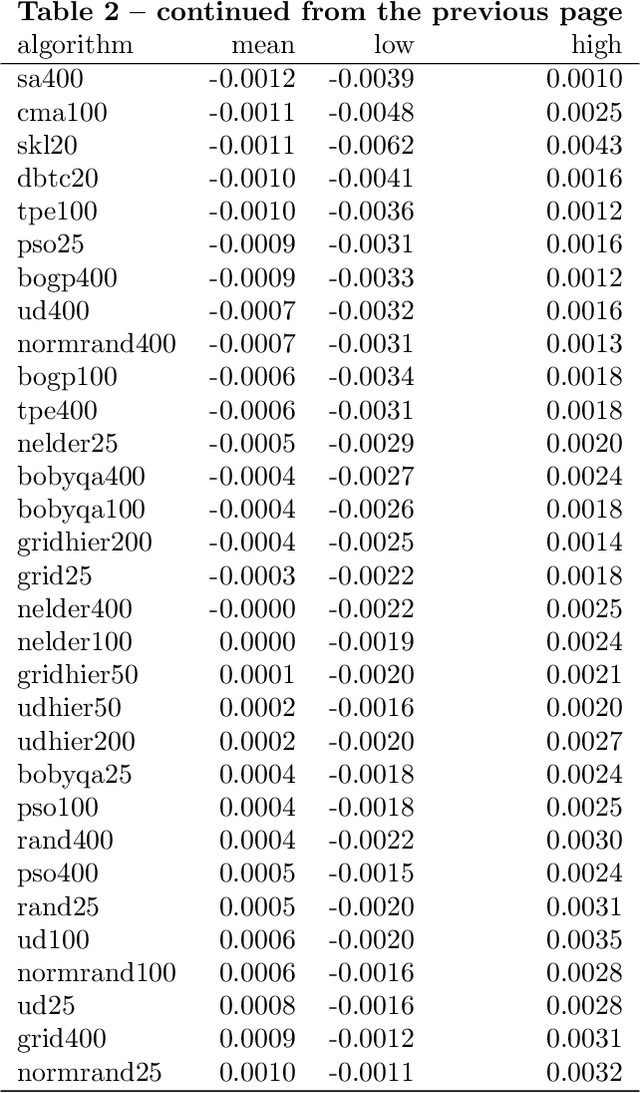
SVM with an RBF kernel is usually one of the best classification algorithms for most data sets, but it is important to tune the two hyperparameters $C$ and $\gamma$ to the data itself. In general, the selection of the hyperparameters is a non-convex optimization problem and thus many algorithms have been proposed to solve it, among them: grid search, random search, Bayesian optimization, simulated annealing, particle swarm optimization, Nelder Mead, and others. There have also been proposals to decouple the selection of $\gamma$ and $C$. We empirically compare 18 of these proposed search algorithms (with different parameterizations for a total of 47 combinations) on 115 real-life binary data sets. We find (among other things) that trees of Parzen estimators and particle swarm optimization select better hyperparameters with only a slight increase in computation time with respect to a grid search with the same number of evaluations. We also find that spending too much computational effort searching the hyperparameters will not likely result in better performance for future data and that there are no significant differences among the different procedures to select the best set of hyperparameters when more than one is found by the search algorithms.

Specialized Support Vector Machines for Open-set Recognition

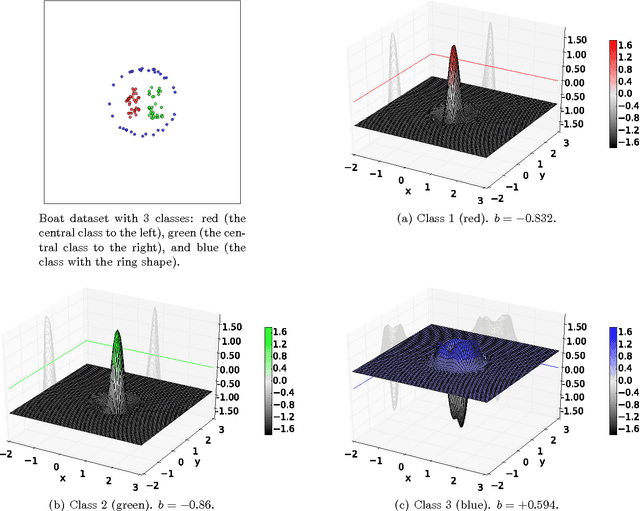
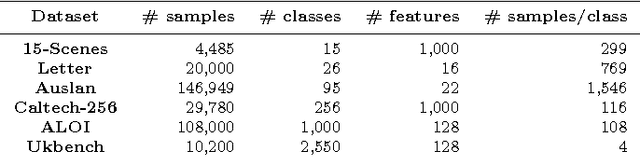
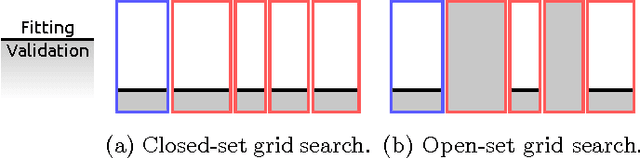
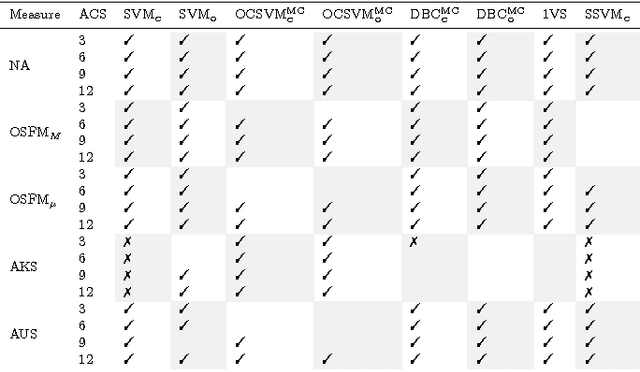
Often, when dealing with real-world recognition problems, we do not need, and often cannot have, knowledge of the entire set of possible classes that might appear during operational testing. Sometimes, some of these classes may be ill-sampled, not sampled at all or undefined. In such cases, we need to think of robust classification methods able to deal with the "unknown" and properly reject samples belonging to classes never seen during training. Notwithstanding, almost all existing classifiers to date were mostly developed for the closed-set scenario, i.e., the classification setup in which it is assumed that all test samples belong to one of the classes with which the classifier was trained. In the open-set scenario, however, a test sample can belong to none of the known classes and the classifier must properly reject it by classifying it as unknown. In this work, we extend upon the well-known Support Vector Machines (SVM) classifier and introduce the Specialized Support Vector Machines (SSVM), which is suitable for recognition in open-set setups. SSVM balances the empirical risk and the risk of the unknown and ensures that the region of the feature space in which a test sample would be classified as known (one of the known classes) is always bounded, ensuring a finite risk of the unknown. The same cannot be guaranteed by the traditional SVM formulation, even when using the Radial Basis Function (RBF) kernel. In this work, we also highlight the properties of the SVM classifier related to the open-set scenario, and provide necessary and sufficient conditions for an RBF SVM to have bounded open-space risk. We also indicate promising directions of investigation of SVM-based methods for open-set scenarios. An extensive set of experiments compares the proposed method with existing solutions in the literature for open-set recognition and the reported results show its effectiveness.

An empirical evaluation of imbalanced data strategies from a practitioner's point of view

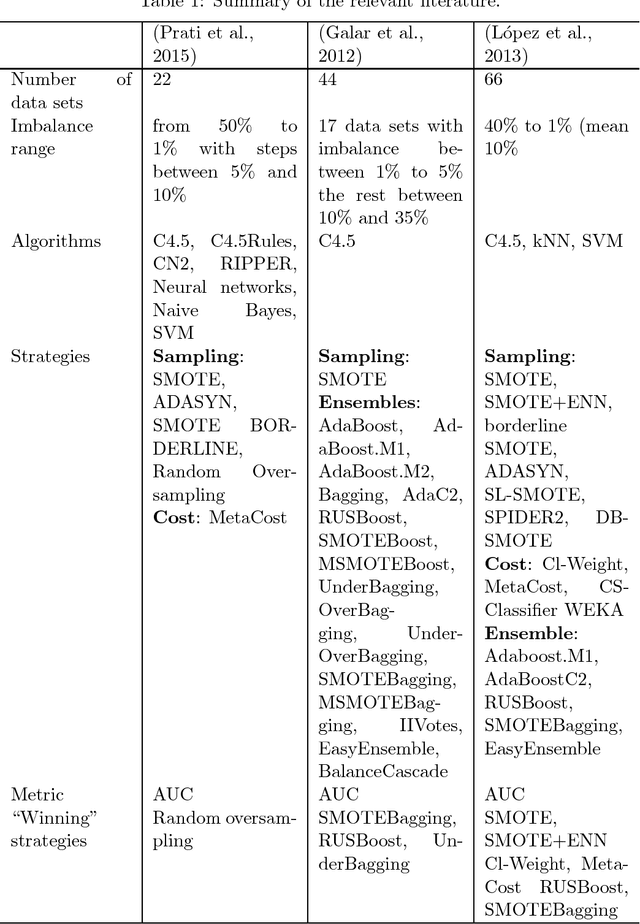
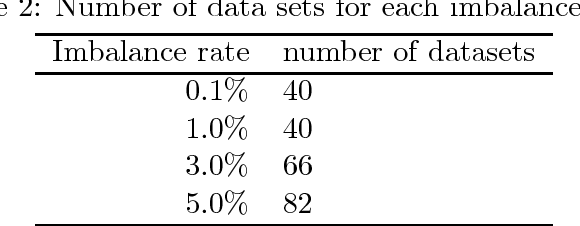
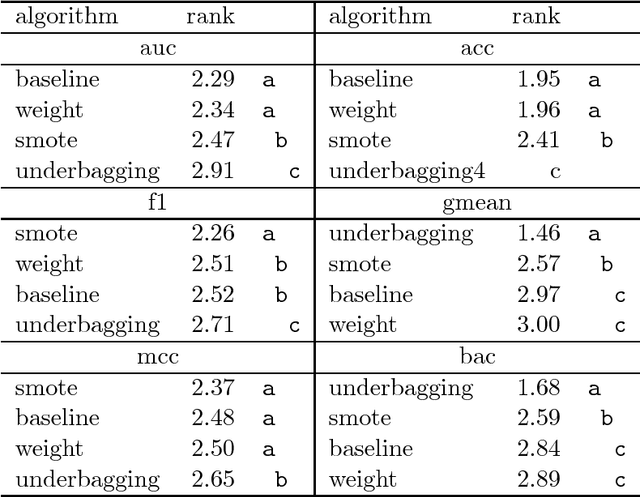
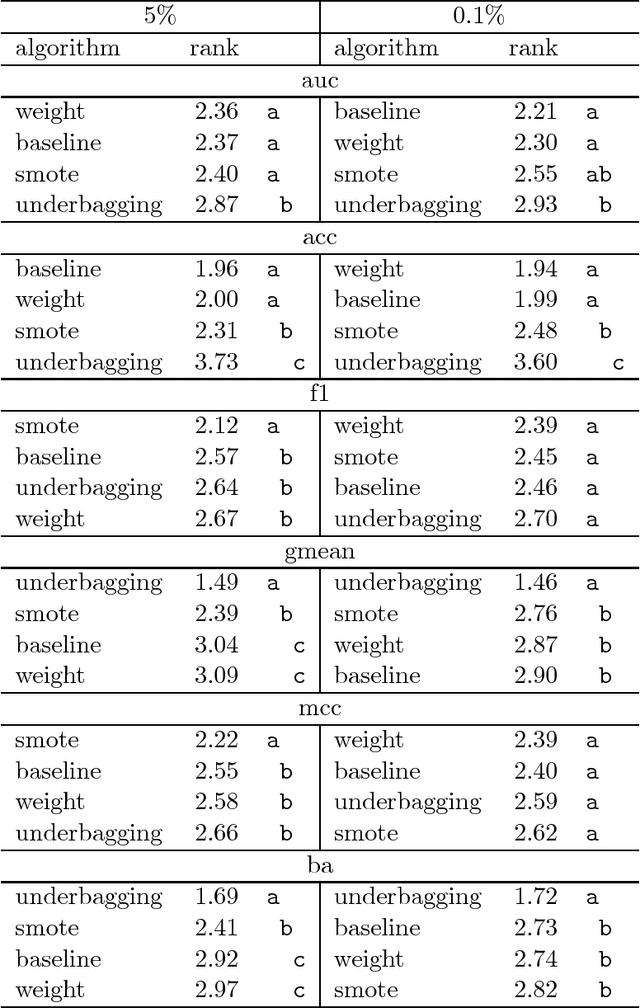
This research tested the following well known strategies to deal with binary imbalanced data on 82 different real life data sets (sampled to imbalance rates of 5%, 3%, 1%, and 0.1%): class weight, SMOTE, Underbagging, and a baseline (just the base classifier). As base classifiers we used SVM with RBF kernel, random forests, and gradient boosting machines and we measured the quality of the resulting classifier using 6 different metrics (Area under the curve, Accuracy, F-measure, G-mean, Matthew's correlation coefficient and Balanced accuracy). The best strategy strongly depends on the metric used to measure the quality of the classifier. For AUC and accuracy class weight and the baseline perform better; for F-measure and MCC, SMOTE performs better; and for G-mean and balanced accuracy, underbagging.

Nested cross-validation when selecting classifiers is overzealous for most practical applications

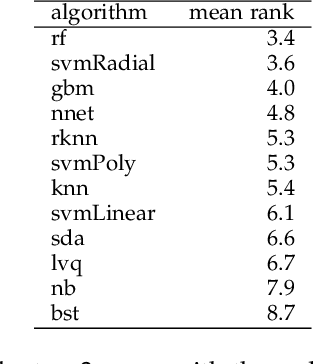
When selecting a classification algorithm to be applied to a particular problem, one has to simultaneously select the best algorithm for that dataset \emph{and} the best set of hyperparameters for the chosen model. The usual approach is to apply a nested cross-validation procedure; hyperparameter selection is performed in the inner cross-validation, while the outer cross-validation computes an unbiased estimate of the expected accuracy of the algorithm \emph{with cross-validation based hyperparameter tuning}. The alternative approach, which we shall call `flat cross-validation', uses a single cross-validation step both to select the optimal hyperparameter values and to provide an estimate of the expected accuracy of the algorithm, that while biased may nevertheless still be used to select the best learning algorithm. We tested both procedures using 12 different algorithms on 115 real life binary datasets and conclude that using the less computationally expensive flat cross-validation procedure will generally result in the selection of an algorithm that is, for all practical purposes, of similar quality to that selected via nested cross-validation, provided the learning algorithms have relatively few hyperparameters to be optimised.

Comparison of 14 different families of classification algorithms on 115 binary datasets

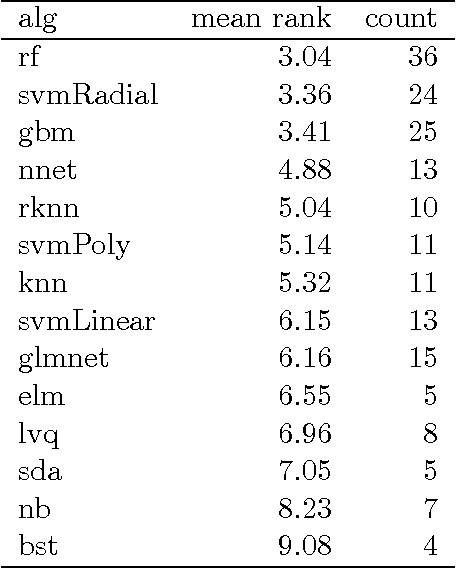
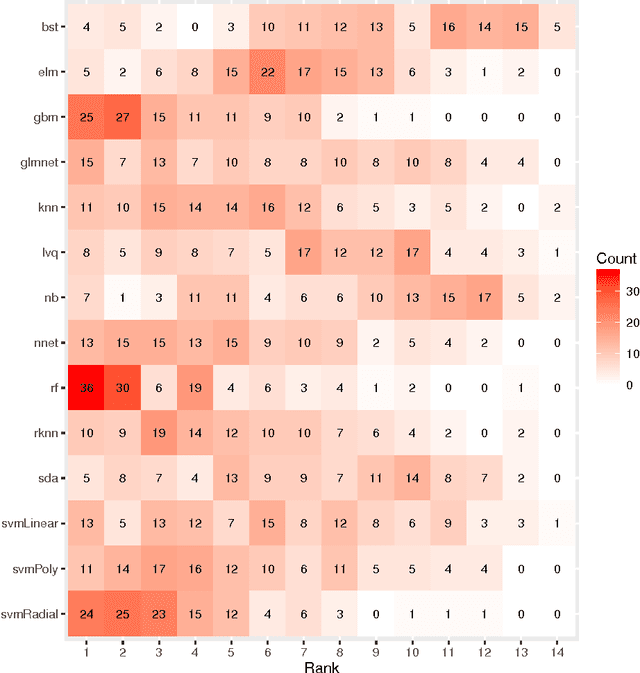
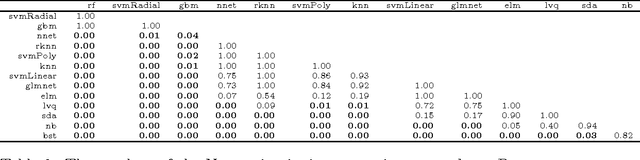
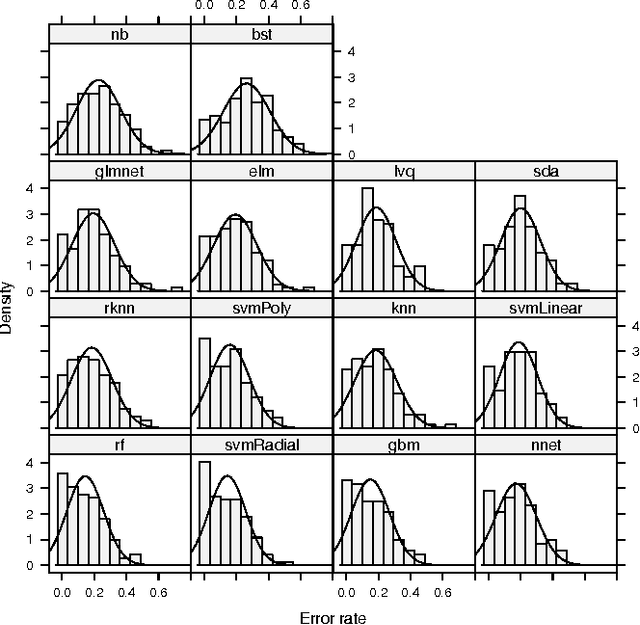
We tested 14 very different classification algorithms (random forest, gradient boosting machines, SVM - linear, polynomial, and RBF - 1-hidden-layer neural nets, extreme learning machines, k-nearest neighbors and a bagging of knn, naive Bayes, learning vector quantization, elastic net logistic regression, sparse linear discriminant analysis, and a boosting of linear classifiers) on 115 real life binary datasets. We followed the Demsar analysis and found that the three best classifiers (random forest, gbm and RBF SVM) are not significantly different from each other. We also discuss that a change of less then 0.0112 in the error rate should be considered as an irrelevant change, and used a Bayesian ANOVA analysis to conclude that with high probability the differences between these three classifiers is not of practical consequence. We also verified the execution time of "standard implementations" of these algorithms and concluded that RBF SVM is the fastest (significantly so) both in training time and in training plus testing time.

Flexible Modeling of Latent Task Structures in Multitask Learning

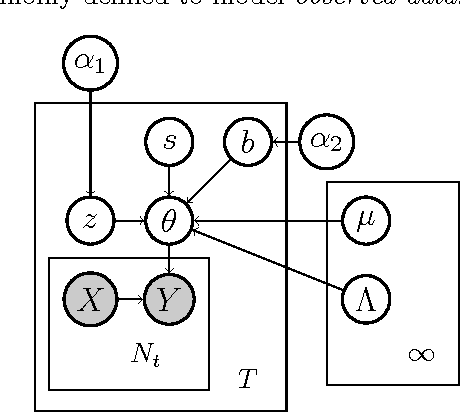
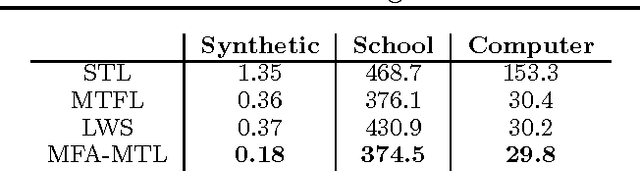
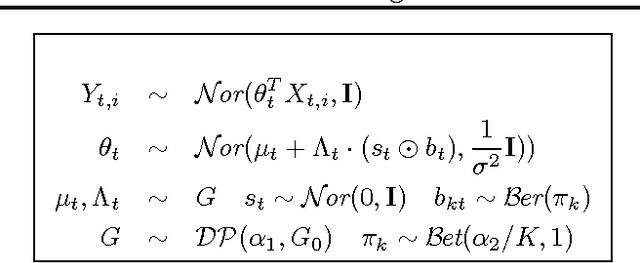
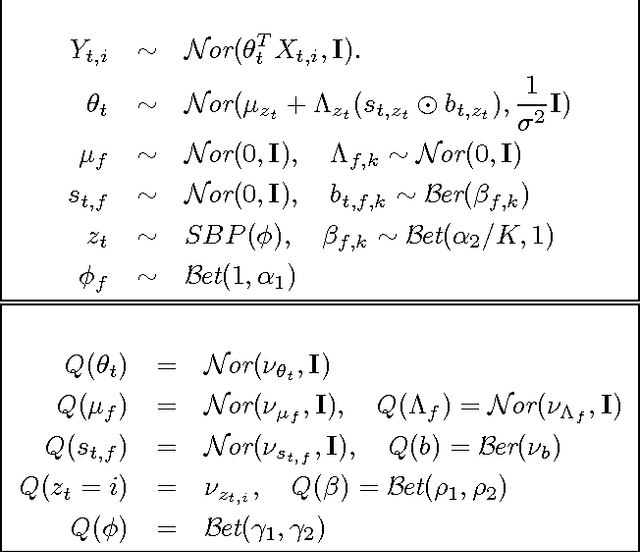
Multitask learning algorithms are typically designed assuming some fixed, a priori known latent structure shared by all the tasks. However, it is usually unclear what type of latent task structure is the most appropriate for a given multitask learning problem. Ideally, the "right" latent task structure should be learned in a data-driven manner. We present a flexible, nonparametric Bayesian model that posits a mixture of factor analyzers structure on the tasks. The nonparametric aspect makes the model expressive enough to subsume many existing models of latent task structures (e.g, mean-regularized tasks, clustered tasks, low-rank or linear/non-linear subspace assumption on tasks, etc.). Moreover, it can also learn more general task structures, addressing the shortcomings of such models. We present a variational inference algorithm for our model. Experimental results on synthetic and real-world datasets, on both regression and classification problems, demonstrate the effectiveness of the proposed method.