A Bayesian Bradley-Terry model to compare multiple ML algorithms on multiple data sets
Paper and Code
Aug 09, 2022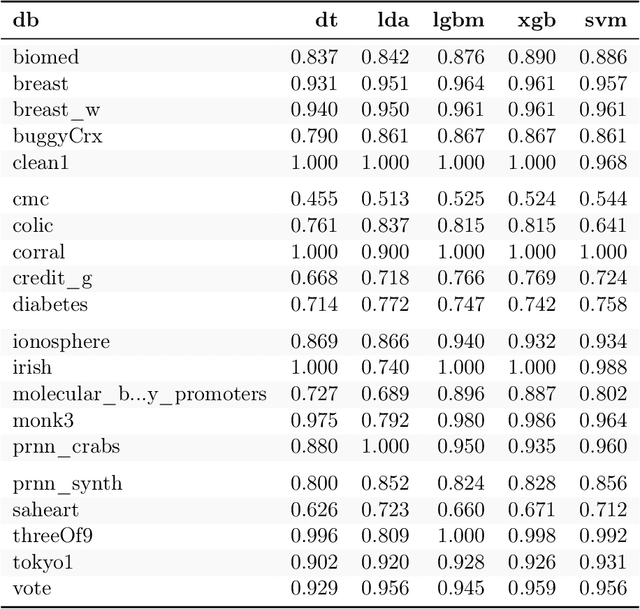
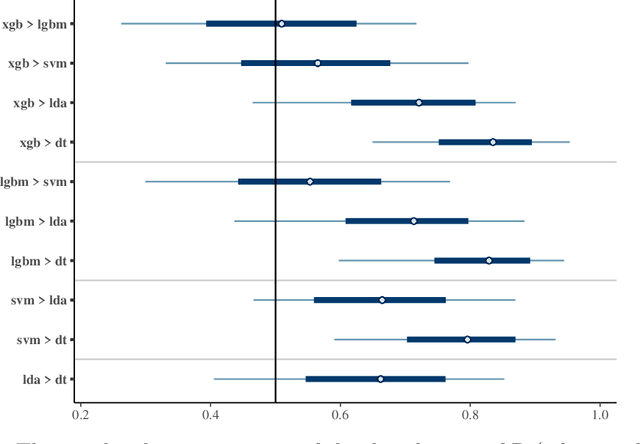
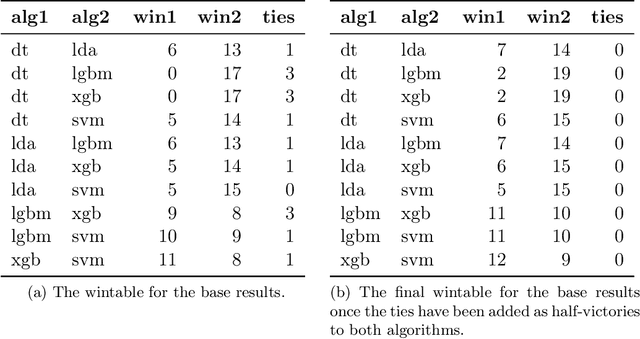
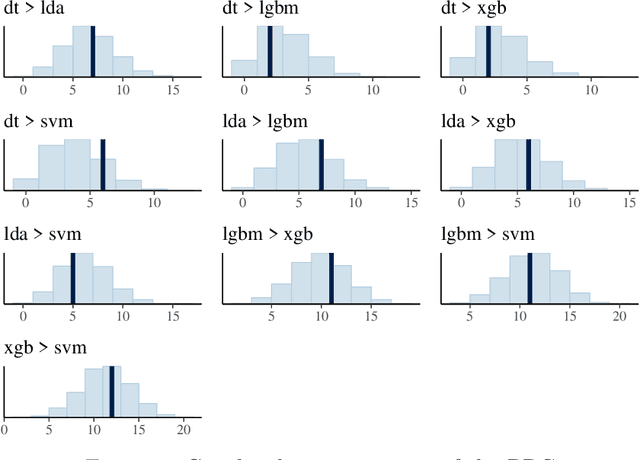
This paper proposes a Bayesian model to compare multiple algorithms on multiple data sets, on any metric. The model is based on the Bradley-Terry model, that counts the number of times one algorithm performs better than another on different data sets. Because of its Bayesian foundations, the Bayesian Bradley Terry model (BBT) has different characteristics than frequentist approaches to comparing multiple algorithms on multiple data sets, such as Demsar (2006) tests on mean rank, and Benavoli et al. (2016) multiple pairwise Wilcoxon tests with p-adjustment procedures. In particular, a Bayesian approach allows for more nuanced statements regarding the algorithms beyond claiming that the difference is or it is not statistically significant. Bayesian approaches also allow to define when two algorithms are equivalent for practical purposes, or the region of practical equivalence (ROPE). Different than a Bayesian signed rank comparison procedure proposed by Benavoli et al. (2017), our approach can define a ROPE for any metric, since it is based on probability statements, and not on differences of that metric. This paper also proposes a local ROPE concept, that evaluates whether a positive difference between a mean measure across some cross validation to the mean of some other algorithms is should be really seen as the first algorithm being better than the second, based on effect sizes. This local ROPE proposal is independent of a Bayesian use, and can be used in frequentist approaches based on ranks. A R package and a Python program that implements the BBT is available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge