Nested cross-validation when selecting classifiers is overzealous for most practical applications
Paper and Code
Sep 25, 2018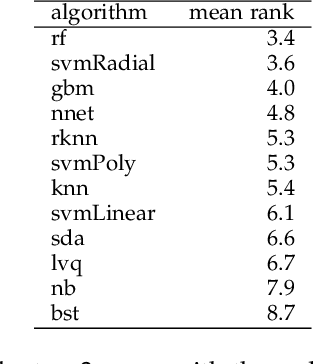



When selecting a classification algorithm to be applied to a particular problem, one has to simultaneously select the best algorithm for that dataset \emph{and} the best set of hyperparameters for the chosen model. The usual approach is to apply a nested cross-validation procedure; hyperparameter selection is performed in the inner cross-validation, while the outer cross-validation computes an unbiased estimate of the expected accuracy of the algorithm \emph{with cross-validation based hyperparameter tuning}. The alternative approach, which we shall call `flat cross-validation', uses a single cross-validation step both to select the optimal hyperparameter values and to provide an estimate of the expected accuracy of the algorithm, that while biased may nevertheless still be used to select the best learning algorithm. We tested both procedures using 12 different algorithms on 115 real life binary datasets and conclude that using the less computationally expensive flat cross-validation procedure will generally result in the selection of an algorithm that is, for all practical purposes, of similar quality to that selected via nested cross-validation, provided the learning algorithms have relatively few hyperparameters to be optimised.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge