Huasen Wu
Decoupled Entity Representation Learning for Pinterest Ads Ranking
Sep 04, 2025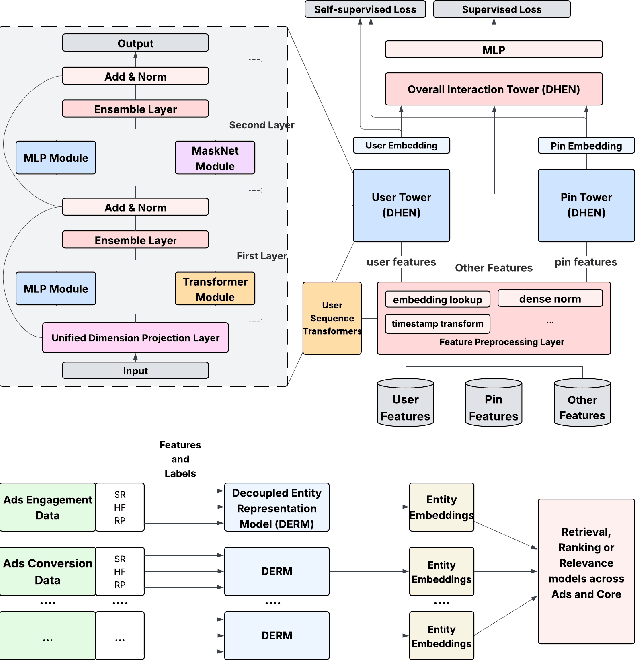



Abstract:In this paper, we introduce a novel framework following an upstream-downstream paradigm to construct user and item (Pin) embeddings from diverse data sources, which are essential for Pinterest to deliver personalized Pins and ads effectively. Our upstream models are trained on extensive data sources featuring varied signals, utilizing complex architectures to capture intricate relationships between users and Pins on Pinterest. To ensure scalability of the upstream models, entity embeddings are learned, and regularly refreshed, rather than real-time computation, allowing for asynchronous interaction between the upstream and downstream models. These embeddings are then integrated as input features in numerous downstream tasks, including ad retrieval and ranking models for CTR and CVR predictions. We demonstrate that our framework achieves notable performance improvements in both offline and online settings across various downstream tasks. This framework has been deployed in Pinterest's production ad ranking systems, resulting in significant gains in online metrics.
Should I send this notification? Optimizing push notifications decision making by modeling the future
Feb 17, 2022Abstract:Most recommender systems are myopic, that is they optimize based on the immediate response of the user. This may be misaligned with the true objective, such as creating long term user satisfaction. In this work we focus on mobile push notifications, where the long term effects of recommender system decisions can be particularly strong. For example, sending too many or irrelevant notifications may annoy a user and cause them to disable notifications. However, a myopic system will always choose to send a notification since negative effects occur in the future. This is typically mitigated using heuristics. However, heuristics can be hard to reason about or improve, require retuning each time the system is changed, and may be suboptimal. To counter these drawbacks, there is significant interest in recommender systems that optimize directly for long-term value (LTV). Here, we describe a method for maximising LTV by using model-based reinforcement learning (RL) to make decisions about whether to send push notifications. We model the effects of sending a notification on the user's future behavior. Much of the prior work applying RL to maximise LTV in recommender systems has focused on session-based optimization, while the time horizon for notification decision making in this work extends over several days. We test this approach in an A/B test on a major social network. We show that by optimizing decisions about push notifications we are able to send less notifications and obtain a higher open rate than the baseline system, while generating the same level of user engagement on the platform as the existing, heuristic-based, system.
Learning to Rank For Push Notifications Using Pairwise Expected Regret
Jan 19, 2022

Abstract:Listwise ranking losses have been widely studied in recommender systems. However, new paradigms of content consumption present new challenges for ranking methods. In this work we contribute an analysis of learning to rank for personalized mobile push notifications and discuss the unique challenges this presents compared to traditional ranking problems. To address these challenges, we introduce a novel ranking loss based on weighting the pairwise loss between candidates by the expected regret incurred for misordering the pair. We demonstrate that the proposed method can outperform prior methods both in a simulated environment and in a production experiment on a major social network.
Waiting but not Aging: Age-of-Information and Utility Optimization Under the Pull Model
Dec 17, 2019



Abstract:The Age-of-Information (AoI) has recently been proposed as an important metric for investigating the timeliness performance in information-update systems. In this paper, we introduce a new Pull model and study the AoI optimization problem under replication schemes. Interestingly, we find that under this new Pull model, replication schemes capture a novel tradeoff between different levels of information freshness and different response times across the servers, which can be exploited to minimize the expected AoI at the user's side. Specifically, assuming Poisson updating process for the servers and exponentially distributed response time, we derive a closed-form formula for computing the expected AoI and obtain the optimal number of responses to wait for to minimize the expected AoI. Then, we extend our analysis to the setting where the user aims to maximize the AoI-based utility, which represents the user's satisfaction level with respect to freshness of the received information. Furthermore, we consider a more realistic scenario where the user has no knowledge of the system. In this case, we reformulate the utility maximization problem as a stochastic Multi-Armed Bandit problem with side observations and leverage the unique structure of the problem to design learning algorithms with improved performance guarantees. Finally, we conduct extensive simulations to elucidate our theoretical results and compare the performance of different algorithms. Our findings reveal that under the Pull model, waiting for more than one response can significantly reduce the AoI and improve the AoI-based utility in most scenarios.
Adaptive Exploration-Exploitation Tradeoff for Opportunistic Bandits
Sep 12, 2017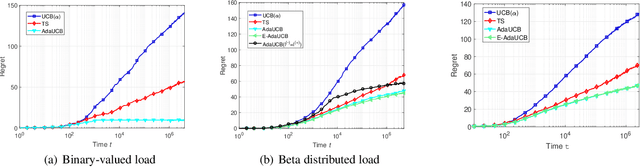
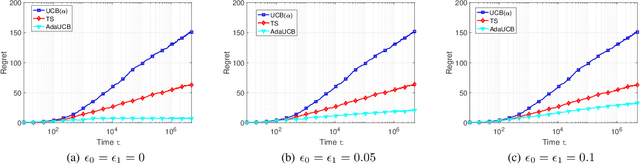
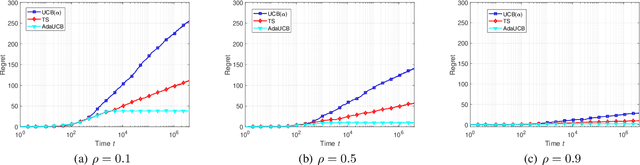
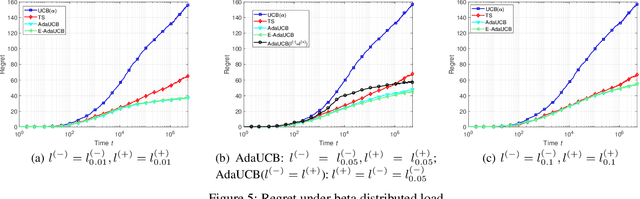
Abstract:In this paper, we propose and study opportunistic bandits - a new variant of bandits where the regret of pulling a suboptimal arm varies under different environmental conditions, such as network load or produce price. When the load/price is low, so is the cost/regret of pulling a suboptimal arm (e.g., trying a suboptimal network configuration). Therefore, intuitively, we could explore more when the load is low and exploit more when the load is high. Inspired by this intuition, we propose an Adaptive Upper-Confidence-Bound (AdaUCB) algorithm to adaptively balance the exploration-exploitation tradeoff for opportunistic bandits. We prove that AdaUCB achieves $O(\log T)$ regret with a smaller coefficient than the traditional UCB algorithm. Furthermore, AdaUCB achieves $O(1)$ regret when the exploration cost is zero if the load level is below a certain threshold. Last, based on both synthetic data and real-world traces, experimental results show that AdaUCB significantly outperforms other bandit algorithms, such as UCB and TS (Thompson Sampling), under large load fluctuations.
Double Thompson Sampling for Dueling Bandits
Oct 27, 2016



Abstract:In this paper, we propose a Double Thompson Sampling (D-TS) algorithm for dueling bandit problems. As indicated by its name, D-TS selects both the first and the second candidates according to Thompson Sampling. Specifically, D-TS maintains a posterior distribution for the preference matrix, and chooses the pair of arms for comparison by sampling twice from the posterior distribution. This simple algorithm applies to general Copeland dueling bandits, including Condorcet dueling bandits as its special case. For general Copeland dueling bandits, we show that D-TS achieves $O(K^2 \log T)$ regret. For Condorcet dueling bandits, we further simplify the D-TS algorithm and show that the simplified D-TS algorithm achieves $O(K \log T + K^2 \log \log T)$ regret. Simulation results based on both synthetic and real-world data demonstrate the efficiency of the proposed D-TS algorithm.
Algorithms with Logarithmic or Sublinear Regret for Constrained Contextual Bandits
Oct 19, 2015

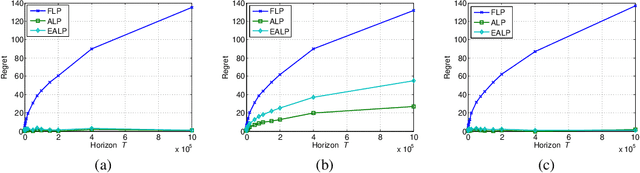
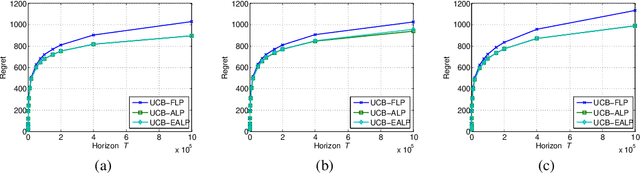
Abstract:We study contextual bandits with budget and time constraints, referred to as constrained contextual bandits.The time and budget constraints significantly complicate the exploration and exploitation tradeoff because they introduce complex coupling among contexts over time.Such coupling effects make it difficult to obtain oracle solutions that assume known statistics of bandits. To gain insight, we first study unit-cost systems with known context distribution. When the expected rewards are known, we develop an approximation of the oracle, referred to Adaptive-Linear-Programming (ALP), which achieves near-optimality and only requires the ordering of expected rewards. With these highly desirable features, we then combine ALP with the upper-confidence-bound (UCB) method in the general case where the expected rewards are unknown {\it a priori}. We show that the proposed UCB-ALP algorithm achieves logarithmic regret except for certain boundary cases. Further, we design algorithms and obtain similar regret analysis results for more general systems with unknown context distribution and heterogeneous costs. To the best of our knowledge, this is the first work that shows how to achieve logarithmic regret in constrained contextual bandits. Moreover, this work also sheds light on the study of computationally efficient algorithms for general constrained contextual bandits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge