Algorithms with Logarithmic or Sublinear Regret for Constrained Contextual Bandits

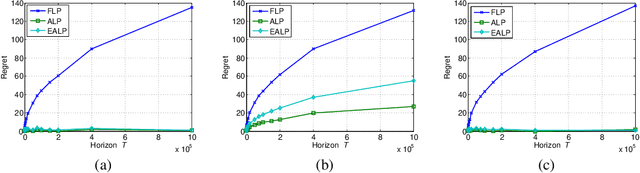
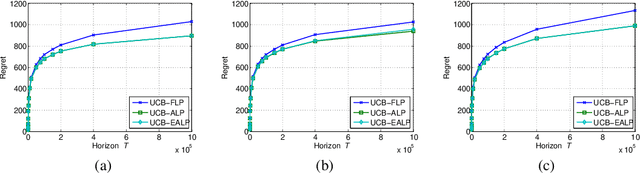
We study contextual bandits with budget and time constraints, referred to as constrained contextual bandits.The time and budget constraints significantly complicate the exploration and exploitation tradeoff because they introduce complex coupling among contexts over time.Such coupling effects make it difficult to obtain oracle solutions that assume known statistics of bandits. To gain insight, we first study unit-cost systems with known context distribution. When the expected rewards are known, we develop an approximation of the oracle, referred to Adaptive-Linear-Programming (ALP), which achieves near-optimality and only requires the ordering of expected rewards. With these highly desirable features, we then combine ALP with the upper-confidence-bound (UCB) method in the general case where the expected rewards are unknown {\it a priori}. We show that the proposed UCB-ALP algorithm achieves logarithmic regret except for certain boundary cases. Further, we design algorithms and obtain similar regret analysis results for more general systems with unknown context distribution and heterogeneous costs. To the best of our knowledge, this is the first work that shows how to achieve logarithmic regret in constrained contextual bandits. Moreover, this work also sheds light on the study of computationally efficient algorithms for general constrained contextual bandits.

Parametrized Stochastic Multi-armed Bandits with Binary Rewards

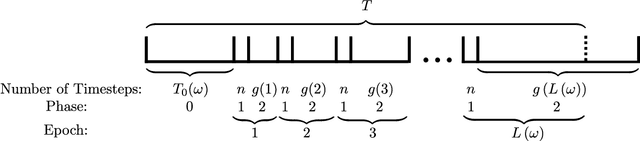
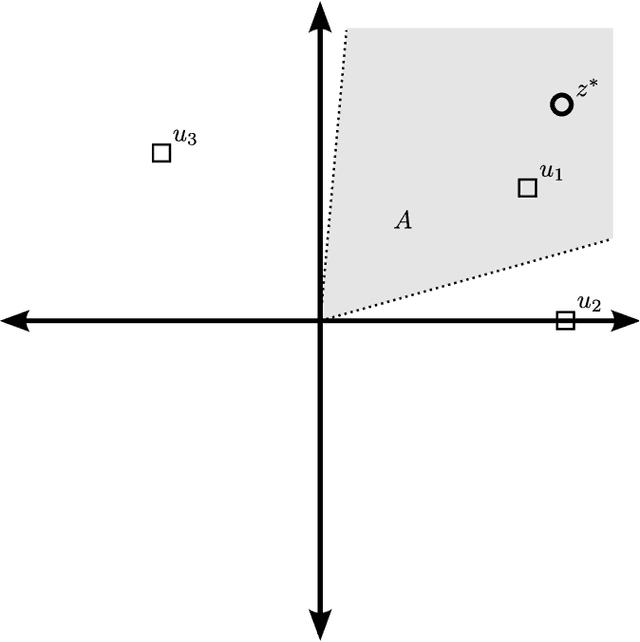
In this paper, we consider the problem of multi-armed bandits with a large, possibly infinite number of correlated arms. We assume that the arms have Bernoulli distributed rewards, independent across time, where the probabilities of success are parametrized by known attribute vectors for each arm, as well as an unknown preference vector, each of dimension $n$. For this model, we seek an algorithm with a total regret that is sub-linear in time and independent of the number of arms. We present such an algorithm, which we call the Two-Phase Algorithm, and analyze its performance. We show upper bounds on the total regret which applies uniformly in time, for both the finite and infinite arm cases. The asymptotics of the finite arm bound show that for any $f \in \omega(\log(T))$, the total regret can be made to be $O(n \cdot f(T))$. In the infinite arm case, the total regret is $O(\sqrt{n^3 T})$.