Hybrid Quantum-inspired Kolmogorov-Arnold Networks for Privacy-Aware Federated Biosignal Learning

Electrocardiogram (ECG) recordings are sensitive biomedical data, limiting the ability of hospitals and wearable devices to share raw signals for centralized model training. Federated learning addresses this practical privacy constraint by enabling collaborative model training while keeping raw biosignal data at their respective sources. However, federated ECG classification remains challenging due to limited client-side samples, imbalanced arrhythmia labels, and non-independent and identically distributed (non-IID) data across clients. These constraints require classifiers that are both communication-efficient and robust to cross-client distribution shifts. In this work, we evaluate a hybrid quantum-inspired Kolmogorov-Arnold network (HQKAN) against a multilayer perceptron (MLP) for five-class arrhythmia classification on the MIT-BIH dataset and three-class classification on the INCART dataset under federated averaging (FedAvg). Across multiple client configurations, HQKAN improves most aggregate and minority-class metrics while using 37.35% fewer trainable parameters and reducing communication cost by 24.89% on MIT-BIH; on INCART, it achieves corresponding reductions of 44.81% and 36.41%. These results indicate that HQKAN offers a compact, communication-efficient and robust alternative to the MLP baseline for privacy-aware federated learning on biosignal data.

Complementary Matrix-Gated QKAN Fast-Weight Programmers for Quantum Dynamics Forecasting

Sequence models must decide what to write into memory and what to retain. In quantum and quantum-inspired sequence learning, nonlinear recurrent updates often require repeated circuit evaluations and sequential backpropagation through time, making long contexts costly. Gated fast-weight programmers (FWPs) based on quantum-inspired Kolmogorov-Arnold networks (QKANs) alleviate this bottleneck by storing context in time-varying fast parameters. However, their scalar gate applies one retention-write balance to every fast-state coordinate, forcing all parameters to share a memory timescale. We introduce Self-Modulating QKAN-based FWPs, which replace this broadcast gate with low-rank-generated element-wise modulation of the new-proposal branch, a bounded old-state branch, or both. We further propose Complementary Matrix Gating (CMG), which uses one sigmoid matrix gate to retain the old state and its complement to write the new proposal. CMG provides coordinate-wise memory control while preserving the bounded convex update and affine prefix-scan structure of scalar gating, at the modulation-head cost of a single-branch rule. We compare four self-modulating rules with scalar gating across four FWP architectures combining classical and QKAN-based slow and fast programmers. Across seven single-step forecasting benchmarks and five sequence lengths, CMG gives the most consistent improvements for architectures whose fast programmer incorporates a QKAN-based module. In direct multi-step forecasting of Jaynes-Cummings and transmon-resonator dynamics simulated with CUDA-Q Dynamics, CMG models maintain mean-squared errors on the order of 0.001 or lower across forecasting horizons of 4, 8, and 16 steps, while improving on their scalar-gated counterparts by at least 91.2%. These results establish coordinate-wise complementary modulation as a stable and effective update for QKAN-based FWPs.

Quantum Variational Activation Functions Empower Kolmogorov-Arnold Networks

Variational quantum circuits (VQCs) are central to quantum machine learning, while recent progress in Kolmogorov-Arnold networks (KANs) highlights the power of learnable activation functions. We unify these directions by introducing quantum variational activation functions (QVAFs), realized through single-qubit data re-uploading circuits called DatA Re-Uploading ActivatioNs (DARUANs). We show that DARUAN with trainable weights in data pre-processing possesses an exponentially growing frequency spectrum with data repetitions, enabling an exponential reduction in parameter size compared with Fourier-based activations without loss of expressivity. Embedding DARUAN into KANs yields quantum-inspired KANs (QKANs), which retain the interpretability of KANs while improving their parameter efficiency, expressivity, and generalization. We further introduce two novel techniques to enhance scalability, feasibility and computational efficiency, such as layer extension and hybrid QKANs (HQKANs) as drop-in replacements of multi-layer perceptrons (MLPs) for feed-forward networks in large-scale models. We provide theoretical analysis and extensive experiments on function regression, image classification, and autoregressive generative language modeling, demonstrating the efficiency and scalability of QKANs. DARUANs and QKANs offer a promising direction for advancing quantum machine learning on both noisy intermediate-scale quantum (NISQ) hardware and classical quantum simulators.

BiSHop: Bi-Directional Cellular Learning for Tabular Data with Generalized Sparse Modern Hopfield Model

We introduce the \textbf{B}i-Directional \textbf{S}parse \textbf{Hop}field Network (\textbf{BiSHop}), a novel end-to-end framework for deep tabular learning. BiSHop handles the two major challenges of deep tabular learning: non-rotationally invariant data structure and feature sparsity in tabular data. Our key motivation comes from the recent established connection between associative memory and attention mechanisms. Consequently, BiSHop uses a dual-component approach, sequentially processing data both column-wise and row-wise through two interconnected directional learning modules. Computationally, these modules house layers of generalized sparse modern Hopfield layers, a sparse extension of the modern Hopfield model with adaptable sparsity. Methodologically, BiSHop facilitates multi-scale representation learning, capturing both intra-feature and inter-feature interactions, with adaptive sparsity at each scale. Empirically, through experiments on diverse real-world datasets, we demonstrate that BiSHop surpasses current SOTA methods with significantly less HPO runs, marking it a robust solution for deep tabular learning.

Variational Quantum Reinforcement Learning via Evolutionary Optimization

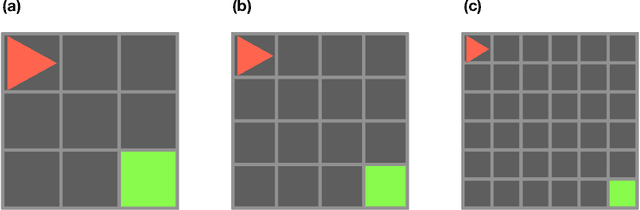
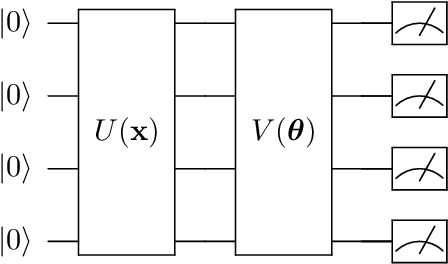
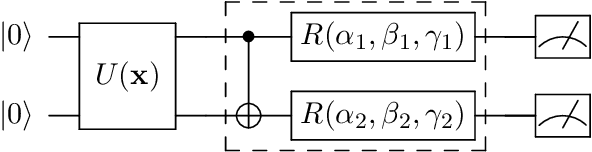
Recent advance in classical reinforcement learning (RL) and quantum computation (QC) points to a promising direction of performing RL on a quantum computer. However, potential applications in quantum RL are limited by the number of qubits available in the modern quantum devices. Here we present two frameworks of deep quantum RL tasks using a gradient-free evolution optimization: First, we apply the amplitude encoding scheme to the Cart-Pole problem; Second, we propose a hybrid framework where the quantum RL agents are equipped with hybrid tensor network-variational quantum circuit (TN-VQC) architecture to handle inputs with dimensions exceeding the number of qubits. This allows us to perform quantum RL on the MiniGrid environment with 147-dimensional inputs. We demonstrate the quantum advantage of parameter saving using the amplitude encoding. The hybrid TN-VQC architecture provides a natural way to perform efficient compression of the input dimension, enabling further quantum RL applications on noisy intermediate-scale quantum devices.

Variational Quantum Circuits for Deep Reinforcement Learning

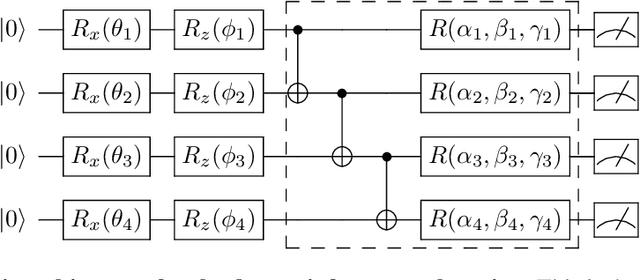
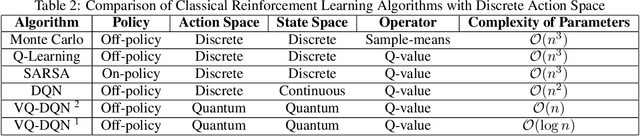
The state-of-the-art Machine learning approaches are based on classical Von-Neumann computing architectures and have been widely used in many industrial and academic domains. With the recent development of quantum computing, a couple of tech-giants have attempted new quantum circuits for machine learning tasks. However, the existing quantum machine learning is hard to simulate classical deep learning models because of the intractability of deep quantum circuits. Thus, it is necessary to design approximated quantum algorithms for quantum machine learning. This work explores variational quantum circuits for deep reinforcement learning. Specifically, we reshape classical deep reinforcement learning algorithms like experience replay and target network into a representation of variational quantum circuits. On the other hand, we use a quantum information encoding scheme to reduce the number of model parameters as small as the scale of $poly(\log{} N)$ in contrast to $poly(N)$ in a standard configuration. Besides, our variational quantum circuits can be deployed in many near-term noisy intermediate quantum machines.