Quantum LEGO Learning: A Modular Design Principle for Hybrid Artificial Intelligence

Hybrid quantum-classical learning models increasingly integrate neural networks with variational quantum circuits (VQCs) to exploit complementary inductive biases. However, many existing approaches rely on tightly coupled architectures or task-specific encoders, limiting conceptual clarity, generality, and transferability across learning settings. In this work, we introduce Quantum LEGO Learning, a modular and architecture-agnostic learning framework that treats classical and quantum components as reusable, composable learning blocks with well-defined roles. Within this framework, a pre-trained classical neural network serves as a frozen feature block, while a VQC acts as a trainable adaptive module that operates on structured representations rather than raw inputs. This separation enables efficient learning under constrained quantum resources and provides a principled abstraction for analyzing hybrid models. We develop a block-wise generalization theory that decomposes learning error into approximation and estimation components, explicitly characterizing how the complexity and training status of each block influence overall performance. Our analysis generalizes prior tensor-network-specific results and identifies conditions under which quantum modules provide representational advantages over comparably sized classical heads. Empirically, we validate the framework through systematic block-swap experiments across frozen feature extractors and both quantum and classical adaptive heads. Experiments on quantum dot classification demonstrate stable optimization, reduced sensitivity to qubit count, and robustness to realistic noise.

Continual Quantum Architecture Search with Tensor-Train Encoding: Theory and Applications to Signal Processing

We introduce CL-QAS, a continual quantum architecture search framework that mitigates the challenges of costly amplitude encoding and catastrophic forgetting in variational quantum circuits. The method uses Tensor-Train encoding to efficiently compress high-dimensional stochastic signals into low-rank quantum feature representations. A bi-loop learning strategy separates circuit parameter optimization from architecture exploration, while an Elastic Weight Consolidation regularization ensures stability across sequential tasks. We derive theoretical upper bounds on approximation, generalization, and robustness under quantum noise, demonstrating that CL-QAS achieves controllable expressivity, sample-efficient generalization, and smooth convergence without barren plateaus. Empirical evaluations on electrocardiogram (ECG)-based signal classification and financial time-series forecasting confirm substantial improvements in accuracy, balanced accuracy, F1 score, and reward. CL-QAS maintains strong forward and backward transfer and exhibits bounded degradation under depolarizing and readout noise, highlighting its potential for adaptive, noise-resilient quantum learning on near-term devices.

Random-Matrix-Induced Simplicity Bias in Over-parameterized Variational Quantum Circuits

Over-parameterization is commonly used to increase the expressivity of variational quantum circuits (VQCs), yet deeper and more highly parameterized circuits often exhibit poor trainability and limited generalization. In this work, we provide a theoretical explanation for this phenomenon from a function-class perspective. We show that sufficiently expressive, unstructured variational ansatze enter a Haar-like universality class in which both observable expectation values and parameter gradients concentrate exponentially with system size. As a consequence, the hypothesis class induced by such circuits collapses with high probability to a narrow family of near-constant functions, a phenomenon we term simplicity bias, with barren plateaus arising as a consequence rather than the root cause. Using tools from random matrix theory and concentration of measure, we rigorously characterize this universality class and establish uniform hypothesis-class collapse over finite datasets. We further show that this collapse is not unavoidable: tensor-structured VQCs, including tensor-network-based and tensor-hypernetwork parameterizations, lie outside the Haar-like universality class. By restricting the accessible unitary ensemble through bounded tensor rank or bond dimension, these architectures prevent concentration of measure, preserve output variability for local observables, and retain non-degenerate gradient signals even in over-parameterized regimes. Together, our results unify barren plateaus, expressivity limits, and generalization collapse under a single structural mechanism rooted in random-matrix universality, highlighting the central role of architectural inductive bias in variational quantum algorithms.

VQC-MLPNet: An Unconventional Hybrid Quantum-Classical Architecture for Scalable and Robust Quantum Machine Learning

Variational Quantum Circuits (VQCs) offer a novel pathway for quantum machine learning, yet their practical application is hindered by inherent limitations such as constrained linear expressivity, optimization challenges, and acute sensitivity to quantum hardware noise. This work introduces VQC-MLPNet, a scalable and robust hybrid quantum-classical architecture designed to overcome these obstacles. By innovatively employing quantum circuits to dynamically generate parameters for classical Multi-Layer Perceptrons (MLPs) via amplitude encoding and parameterized quantum operations, VQC-MLPNet substantially expands representation capabilities and augments training stability. We provide rigorous theoretical guarantees via statistical learning techniques and Neural Tangent Kernel analysis, explicitly deriving upper bounds on approximation, uniform deviation, and optimization errors. These theoretical insights demonstrate exponential improvements in representation capacity relative to quantum circuit depth and the number of qubits, providing clear computational advantages over standalone quantum circuits and existing hybrid quantum architectures. Our theoretical claims are empirically corroborated through extensive experiments, including classifying semiconductor quantum-dot charge states and predicting genomic transcription factor binding sites, demonstrating resilient performance even under realistic IBM quantum noise simulations. This research establishes a theoretically sound and practically robust framework, advancing the frontiers of quantum-enhanced learning for unconventional computing paradigms in the Noisy Intermediate-Scale Quantum era and beyond.

Quantum Machine Learning: An Interplay Between Quantum Computing and Machine Learning

Quantum machine learning (QML) is a rapidly growing field that combines quantum computing principles with traditional machine learning. It seeks to revolutionize machine learning by harnessing the unique capabilities of quantum mechanics and employs machine learning techniques to advance quantum computing research. This paper introduces quantum computing for the machine learning paradigm, where variational quantum circuits (VQC) are used to develop QML architectures on noisy intermediate-scale quantum (NISQ) devices. We discuss machine learning for the quantum computing paradigm, showcasing our recent theoretical and empirical findings. In particular, we delve into future directions for studying QML, exploring the potential industrial impacts of QML research.

Leveraging Pre-Trained Neural Networks to Enhance Machine Learning with Variational Quantum Circuits

Quantum Machine Learning (QML) offers tremendous potential but is currently limited by the availability of qubits. We introduce an innovative approach that utilizes pre-trained neural networks to enhance Variational Quantum Circuits (VQC). This technique effectively separates approximation error from qubit count and removes the need for restrictive conditions, making QML more viable for real-world applications. Our method significantly improves parameter optimization for VQC while delivering notable gains in representation and generalization capabilities, as evidenced by rigorous theoretical analysis and extensive empirical testing on quantum dot classification tasks. Moreover, our results extend to applications such as human genome analysis, demonstrating the broad applicability of our approach. By addressing the constraints of current quantum hardware, our work paves the way for a new era of advanced QML applications, unlocking the full potential of quantum computing in fields such as machine learning, materials science, medicine, mimetics, and various interdisciplinary areas.

Spatio-Temporal Similarity Measure based Multi-Task Learning for Predicting Alzheimer's Disease Progression using MRI Data

Identifying and utilising various biomarkers for tracking Alzheimer's disease (AD) progression have received many recent attentions and enable helping clinicians make the prompt decisions. Traditional progression models focus on extracting morphological biomarkers in regions of interest (ROIs) from MRI/PET images, such as regional average cortical thickness and regional volume. They are effective but ignore the relationships between brain ROIs over time, which would lead to synergistic deterioration. For exploring the synergistic deteriorating relationship between these biomarkers, in this paper, we propose a novel spatio-temporal similarity measure based multi-task learning approach for effectively predicting AD progression and sensitively capturing the critical relationships between biomarkers. Specifically, we firstly define a temporal measure for estimating the magnitude and velocity of biomarker change over time, which indicate a changing trend(temporal). Converting this trend into the vector, we then compare this variability between biomarkers in a unified vector space(spatial). The experimental results show that compared with directly ROI based learning, our proposed method is more effective in predicting disease progression. Our method also enables performing longitudinal stability selection to identify the changing relationships between biomarkers, which play a key role in disease progression. We prove that the synergistic deteriorating biomarkers between cortical volumes or surface areas have a significant effect on the cognitive prediction.

Optimizing Quantum Federated Learning Based on Federated Quantum Natural Gradient Descent

Quantum federated learning (QFL) is a quantum extension of the classical federated learning model across multiple local quantum devices. An efficient optimization algorithm is always expected to minimize the communication overhead among different quantum participants. In this work, we propose an efficient optimization algorithm, namely federated quantum natural gradient descent (FQNGD), and further, apply it to a QFL framework that is composed of a variational quantum circuit (VQC)-based quantum neural networks (QNN). Compared with stochastic gradient descent methods like Adam and Adagrad, the FQNGD algorithm admits much fewer training iterations for the QFL to get converged. Moreover, it can significantly reduce the total communication overhead among local quantum devices. Our experiments on a handwritten digit classification dataset justify the effectiveness of the FQNGD for the QFL framework in terms of a faster convergence rate on the training set and higher accuracy on the test set.

An Ensemble Teacher-Student Learning Approach with Poisson Sub-sampling to Differential Privacy Preserving Speech Recognition

We propose an ensemble learning framework with Poisson sub-sampling to effectively train a collection of teacher models to issue some differential privacy (DP) guarantee for training data. Through boosting under DP, a student model derived from the training data suffers little model degradation from the models trained with no privacy protection. Our proposed solution leverages upon two mechanisms, namely: (i) a privacy budget amplification via Poisson sub-sampling to train a target prediction model that requires less noise to achieve a same level of privacy budget, and (ii) a combination of the sub-sampling technique and an ensemble teacher-student learning framework that introduces DP-preserving noise at the output of the teacher models and transfers DP-preserving properties via noisy labels. Privacy-preserving student models are then trained with the noisy labels to learn the knowledge with DP-protection from the teacher model ensemble. Experimental evidences on spoken command recognition and continuous speech recognition of Mandarin speech show that our proposed framework greatly outperforms existing DP-preserving algorithms in both speech processing tasks.

Theoretical Error Performance Analysis for Variational Quantum Circuit Based Functional Regression

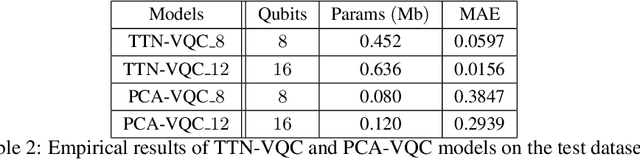
The noisy intermediate-scale quantum (NISQ) devices enable the implementation of the variational quantum circuit (VQC) for quantum neural networks (QNN). Although the VQC-based QNN has succeeded in many machine learning tasks, the representation and generalization powers of VQC still require further investigation, particularly when the dimensionality reduction of classical inputs is concerned. In this work, we first put forth an end-to-end quantum neural network, namely, TTN-VQC, which consists of a quantum tensor network based on a tensor-train network (TTN) for dimensionality reduction and a VQC for functional regression. Then, we aim at the error performance analysis for the TTN-VQC in terms of representation and generalization powers. We also characterize the optimization properties of TTN-VQC by leveraging the Polyak-Lojasiewicz (PL) condition. Moreover, we conduct the experiments of functional regression on a handwritten digit classification dataset to justify our theoretical analysis.