The UEA multivariate time series classification archive, 2018

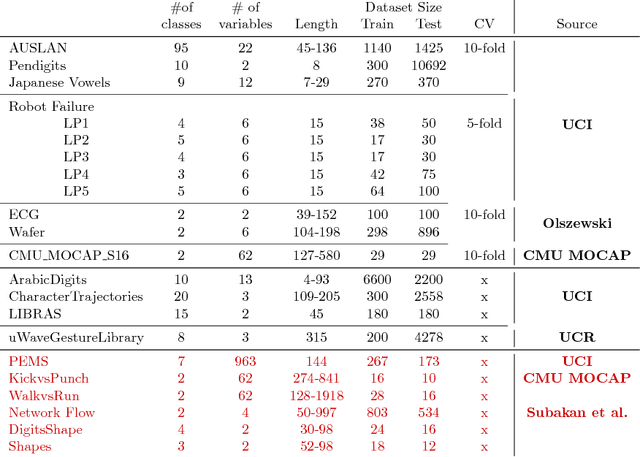
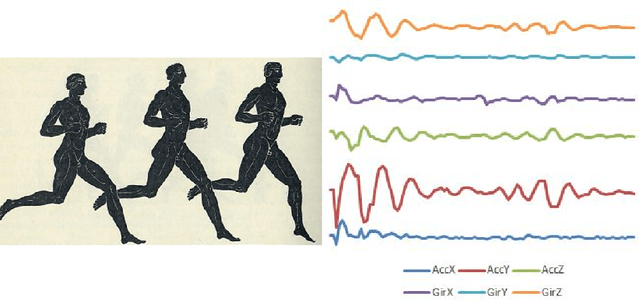
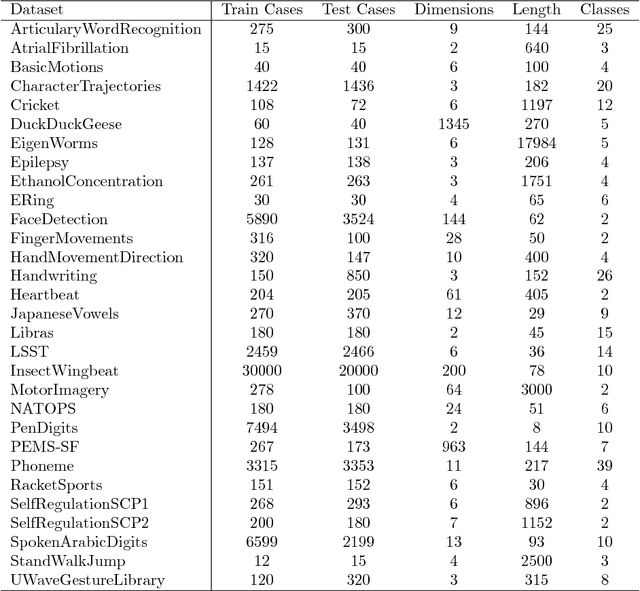
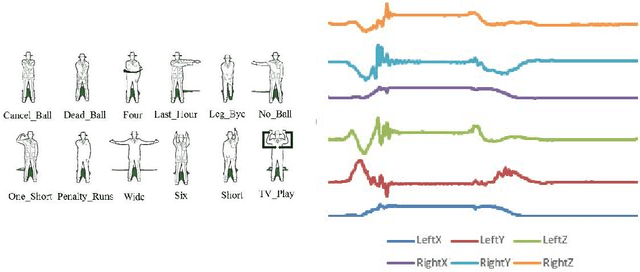
In 2002, the UCR time series classification archive was first released with sixteen datasets. It gradually expanded, until 2015 when it increased in size from 45 datasets to 85 datasets. In October 2018 more datasets were added, bringing the total to 128. The new archive contains a wide range of problems, including variable length series, but it still only contains univariate time series classification problems. One of the motivations for introducing the archive was to encourage researchers to perform a more rigorous evaluation of newly proposed time series classification (TSC) algorithms. It has worked: most recent research into TSC uses all 85 datasets to evaluate algorithmic advances. Research into multivariate time series classification, where more than one series are associated with each class label, is in a position where univariate TSC research was a decade ago. Algorithms are evaluated using very few datasets and claims of improvement are not based on statistical comparisons. We aim to address this problem by forming the first iteration of the MTSC archive, to be hosted at the website www.timeseriesclassification.com. Like the univariate archive, this formulation was a collaborative effort between researchers at the University of East Anglia (UEA) and the University of California, Riverside (UCR). The 2018 vintage consists of 30 datasets with a wide range of cases, dimensions and series lengths. For this first iteration of the archive we format all data to be of equal length, include no series with missing data and provide train/test splits.

The UCR Time Series Archive

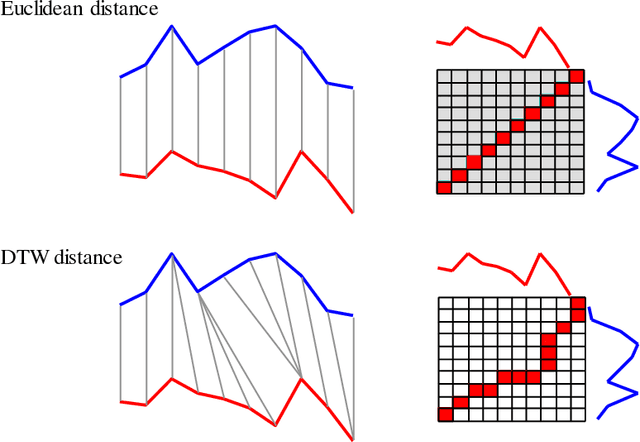
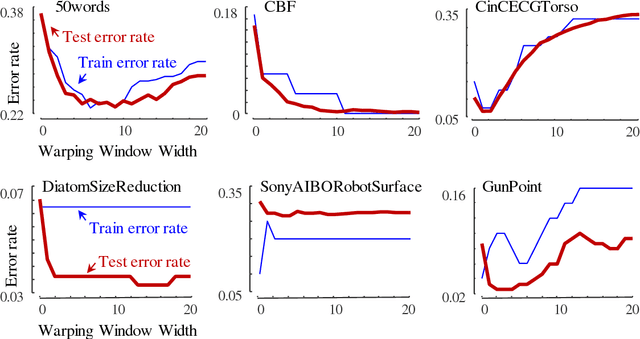
The UCR Time Series Archive - introduced in 2002, has become an important resource in the time series data mining community, with at least one thousand published papers making use of at least one dataset from the archive. The original incarnation of the archive had sixteen datasets but since that time, it has gone through periodic expansions. The last expansion took place in the summer of 2015 when the archive grew from 45 datasets to 85 datasets. This paper introduces and will focus on the new data expansion from 85 to 128 datasets. Beyond expanding this valuable resource, this paper offers pragmatic advice to anyone who may wish to evaluate a new algorithm on the archive. Finally, this paper makes a novel and yet actionable claim: of the hundreds of papers that show an improvement over the standard baseline (1-Nearest Neighbor classification), a large fraction may be misattributing the reasons for their improvement. Moreover, they may have been able to achieve the same improvement with a much simpler modification, requiring just a single line of code.

A General Framework for Density Based Time Series Clustering Exploiting a Novel Admissible Pruning Strategy

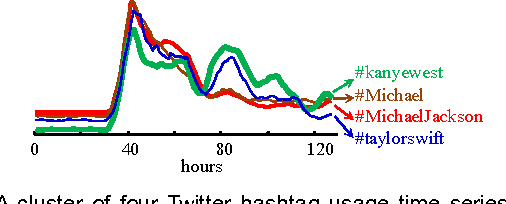
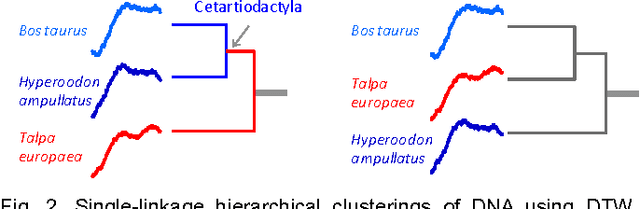
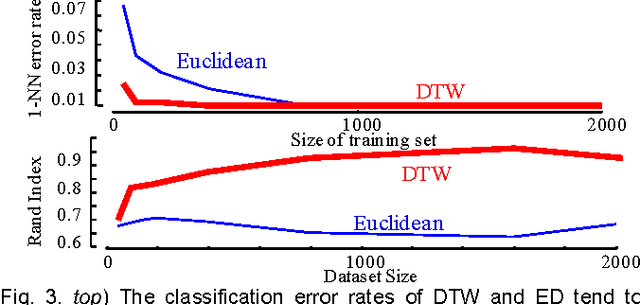
Time Series Clustering is an important subroutine in many higher-level data mining analyses, including data editing for classifiers, summarization, and outlier detection. It is well known that for similarity search the superiority of Dynamic Time Warping (DTW) over Euclidean distance gradually diminishes as we consider ever larger datasets. However, as we shall show, the same is not true for clustering. Clustering time series under DTW remains a computationally expensive operation. In this work, we address this issue in two ways. We propose a novel pruning strategy that exploits both the upper and lower bounds to prune off a very large fraction of the expensive distance calculations. This pruning strategy is admissible and gives us provably identical results to the brute force algorithm, but is at least an order of magnitude faster. For datasets where even this level of speedup is inadequate, we show that we can use a simple heuristic to order the unavoidable calculations in a most-useful-first ordering, thus casting the clustering into an anytime framework. We demonstrate the utility of our ideas with both single and multidimensional case studies in the domains of astronomy, speech physiology, medicine and entomology. In addition, we show the generality of our clustering framework to other domains by efficiently obtaining semantically significant clusters in protein sequences using the Edit Distance, the discrete data analogue of DTW.