Nurjahan Begum
A General Framework for Density Based Time Series Clustering Exploiting a Novel Admissible Pruning Strategy
Dec 02, 2016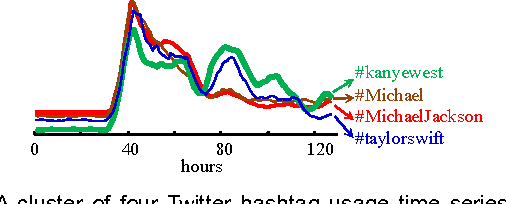
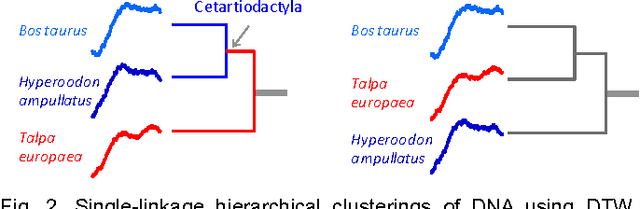
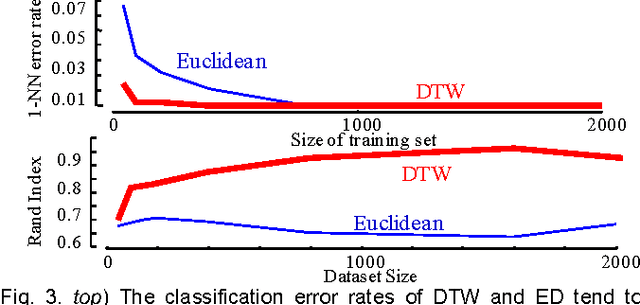

Abstract:Time Series Clustering is an important subroutine in many higher-level data mining analyses, including data editing for classifiers, summarization, and outlier detection. It is well known that for similarity search the superiority of Dynamic Time Warping (DTW) over Euclidean distance gradually diminishes as we consider ever larger datasets. However, as we shall show, the same is not true for clustering. Clustering time series under DTW remains a computationally expensive operation. In this work, we address this issue in two ways. We propose a novel pruning strategy that exploits both the upper and lower bounds to prune off a very large fraction of the expensive distance calculations. This pruning strategy is admissible and gives us provably identical results to the brute force algorithm, but is at least an order of magnitude faster. For datasets where even this level of speedup is inadequate, we show that we can use a simple heuristic to order the unavoidable calculations in a most-useful-first ordering, thus casting the clustering into an anytime framework. We demonstrate the utility of our ideas with both single and multidimensional case studies in the domains of astronomy, speech physiology, medicine and entomology. In addition, we show the generality of our clustering framework to other domains by efficiently obtaining semantically significant clusters in protein sequences using the Edit Distance, the discrete data analogue of DTW.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge