1-D CNN-Based Online Signature Verification with Federated Learning

Online signature verification plays a pivotal role in security infrastructures. However, conventional online signature verification models pose significant risks to data privacy, especially during training processes. To mitigate these concerns, we propose a novel federated learning framework that leverages 1-D Convolutional Neural Networks (CNN) for online signature verification. Furthermore, our experiments demonstrate the effectiveness of our framework regarding 1-D CNN and federated learning. Particularly, the experiment results highlight that our framework 1) minimizes local computational resources; 2) enhances transfer effects with substantial initialization data; 3) presents remarkable scalability. The centralized 1-D CNN model achieves an Equal Error Rate (EER) of 3.33% and an accuracy of 96.25%. Meanwhile, configurations with 2, 5, and 10 agents yield EERs of 5.42%, 5.83%, and 5.63%, along with accuracies of 95.21%, 94.17%, and 94.06%, respectively.

Dr.Hair: Reconstructing Scalp-Connected Hair Strands without Pre-training via Differentiable Rendering of Line Segments

In the film and gaming industries, achieving a realistic hair appearance typically involves the use of strands originating from the scalp. However, reconstructing these strands from observed surface images of hair presents significant challenges. The difficulty in acquiring Ground Truth (GT) data has led state-of-the-art learning-based methods to rely on pre-training with manually prepared synthetic CG data. This process is not only labor-intensive and costly but also introduces complications due to the domain gap when compared to real-world data. In this study, we propose an optimization-based approach that eliminates the need for pre-training. Our method represents hair strands as line segments growing from the scalp and optimizes them using a novel differentiable rendering algorithm. To robustly optimize a substantial number of slender explicit geometries, we introduce 3D orientation estimation utilizing global optimization, strand initialization based on Laplace's equation, and reparameterization that leverages geometric connectivity and spatial proximity. Unlike existing optimization-based methods, our method is capable of reconstructing internal hair flow in an absolute direction. Our method exhibits robust and accurate inverse rendering, surpassing the quality of existing methods and significantly improving processing speed.

BlockFusion: Expandable 3D Scene Generation using Latent Tri-plane Extrapolation

We present BlockFusion, a diffusion-based model that generates 3D scenes as unit blocks and seamlessly incorporates new blocks to extend the scene. BlockFusion is trained using datasets of 3D blocks that are randomly cropped from complete 3D scene meshes. Through per-block fitting, all training blocks are converted into the hybrid neural fields: with a tri-plane containing the geometry features, followed by a Multi-layer Perceptron (MLP) for decoding the signed distance values. A variational auto-encoder is employed to compress the tri-planes into the latent tri-plane space, on which the denoising diffusion process is performed. Diffusion applied to the latent representations allows for high-quality and diverse 3D scene generation. To expand a scene during generation, one needs only to append empty blocks to overlap with the current scene and extrapolate existing latent tri-planes to populate new blocks. The extrapolation is done by conditioning the generation process with the feature samples from the overlapping tri-planes during the denoising iterations. Latent tri-plane extrapolation produces semantically and geometrically meaningful transitions that harmoniously blend with the existing scene. A 2D layout conditioning mechanism is used to control the placement and arrangement of scene elements. Experimental results indicate that BlockFusion is capable of generating diverse, geometrically consistent and unbounded large 3D scenes with unprecedented high-quality shapes in both indoor and outdoor scenarios.

Dressi: A Hardware-Agnostic Differentiable Renderer with Reactive Shader Packing and Soft Rasterization

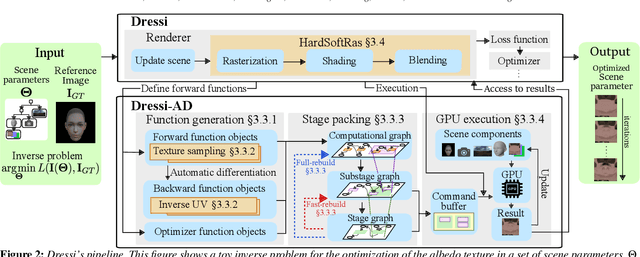
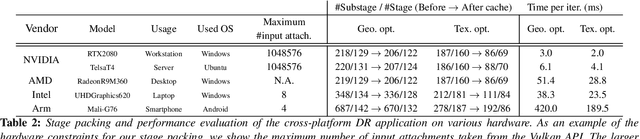
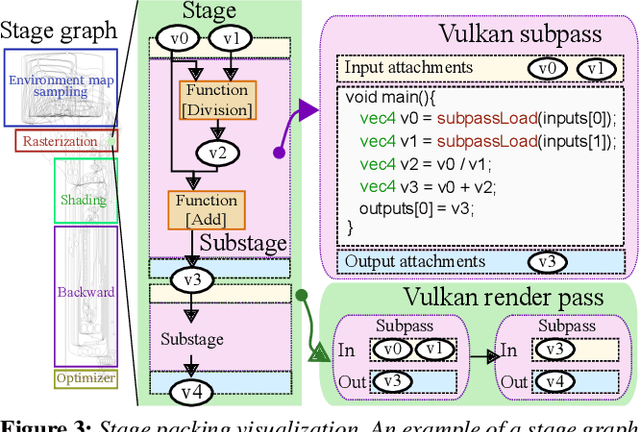
Differentiable rendering (DR) enables various computer graphics and computer vision applications through gradient-based optimization with derivatives of the rendering equation. Most rasterization-based approaches are built on general-purpose automatic differentiation (AD) libraries and DR-specific modules handcrafted using CUDA. Such a system design mixes DR algorithm implementation and algorithm building blocks, resulting in hardware dependency and limited performance. In this paper, we present a practical hardware-agnostic differentiable renderer called Dressi, which is based on a new full AD design. The DR algorithms of Dressi are fully written in our Vulkan-based AD for DR, Dressi-AD, which supports all primitive operations for DR. Dressi-AD and our inverse UV technique inside it bring hardware independence and acceleration by graphics hardware. Stage packing, our runtime optimization technique, can adapt hardware constraints and efficiently execute complex computational graphs of DR with reactive cache considering the render pass hierarchy of Vulkan. HardSoftRas, our novel rendering process, is designed for inverse rendering with a graphics pipeline. Under the limited functionalities of the graphics pipeline, HardSoftRas can propagate the gradients of pixels from the screen space to far-range triangle attributes. Our experiments and applications demonstrate that Dressi establishes hardware independence, high-quality and robust optimization with fast speed, and photorealistic rendering.

Riemannian stochastic quasi-Newton algorithm with variance reduction and its convergence analysis

Stochastic variance reduction algorithms have recently become popular for minimizing the average of a large, but finite number of loss functions. The present paper proposes a Riemannian stochastic quasi-Newton algorithm with variance reduction (R-SQN-VR). The key challenges of averaging, adding, and subtracting multiple gradients are addressed with notions of retraction and vector transport. We present convergence analyses of R-SQN-VR on both non-convex and retraction-convex functions under retraction and vector transport operators. The proposed algorithm is evaluated on the Karcher mean computation on the symmetric positive-definite manifold and the low-rank matrix completion on the Grassmann manifold. In all cases, the proposed algorithm outperforms the state-of-the-art Riemannian batch and stochastic gradient algorithms.

Riemannian stochastic variance reduced gradient

Stochastic variance reduction algorithms have recently become popular for minimizing the average of a large but finite number of loss functions. In this paper, we propose a novel Riemannian extension of the Euclidean stochastic variance reduced gradient algorithm (R-SVRG) to a manifold search space. The key challenges of averaging, adding, and subtracting multiple gradients are addressed with retraction and vector transport. We present a global convergence analysis of the proposed algorithm with a decay step size and a local convergence rate analysis under a fixed step size under some natural assumptions. The proposed algorithm is applied to problems on the Grassmann manifold, such as principal component analysis, low-rank matrix completion, and computation of the Karcher mean of subspaces, and outperforms the standard Riemannian stochastic gradient descent algorithm in each case.

Riemannian stochastic variance reduced gradient on Grassmann manifold

Stochastic variance reduction algorithms have recently become popular for minimizing the average of a large, but finite, number of loss functions. In this paper, we propose a novel Riemannian extension of the Euclidean stochastic variance reduced gradient algorithm (R-SVRG) to a compact manifold search space. To this end, we show the developments on the Grassmann manifold. The key challenges of averaging, addition, and subtraction of multiple gradients are addressed with notions like logarithm mapping and parallel translation of vectors on the Grassmann manifold. We present a global convergence analysis of the proposed algorithm with decay step-sizes and a local convergence rate analysis under fixed step-size with some natural assumptions. The proposed algorithm is applied on a number of problems on the Grassmann manifold like principal components analysis, low-rank matrix completion, and the Karcher mean computation. In all these cases, the proposed algorithm outperforms the standard Riemannian stochastic gradient descent algorithm.