Hiroyuki Kasai
Navigating the Exploration-Exploitation Tradeoff in Inference-Time Scaling of Diffusion Models
Aug 17, 2025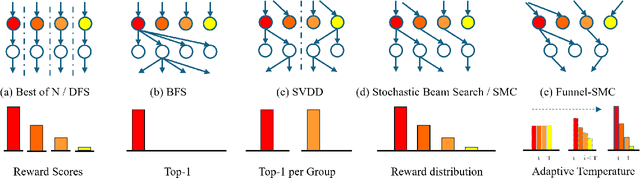

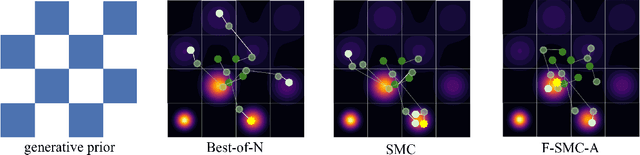
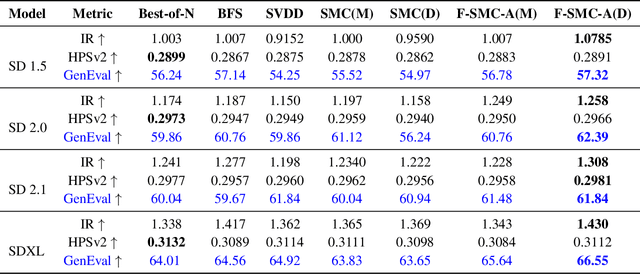
Abstract:Inference-time scaling has achieved remarkable success in language models, yet its adaptation to diffusion models remains underexplored. We observe that the efficacy of recent Sequential Monte Carlo (SMC)-based methods largely stems from globally fitting the The reward-tilted distribution, which inherently preserves diversity during multi-modal search. However, current applications of SMC to diffusion models face a fundamental dilemma: early-stage noise samples offer high potential for improvement but are difficult to evaluate accurately, whereas late-stage samples can be reliably assessed but are largely irreversible. To address this exploration-exploitation trade-off, we approach the problem from the perspective of the search algorithm and propose two strategies: Funnel Schedule and Adaptive Temperature. These simple yet effective methods are tailored to the unique generation dynamics and phase-transition behavior of diffusion models. By progressively reducing the number of maintained particles and down-weighting the influence of early-stage rewards, our methods significantly enhance sample quality without increasing the total number of Noise Function Evaluations. Experimental results on multiple benchmarks and state-of-the-art text-to-image diffusion models demonstrate that our approach outperforms previous baselines.
Self-supervised Subgraph Neural Network With Deep Reinforcement Walk Exploration
Feb 03, 2025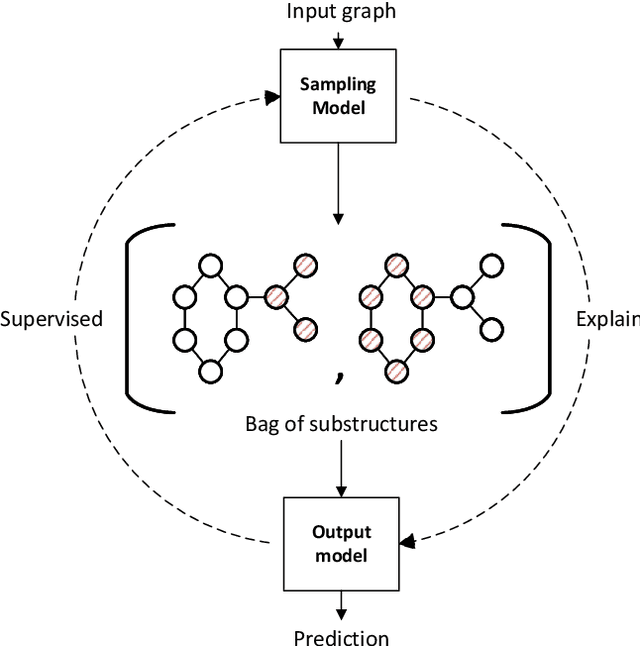
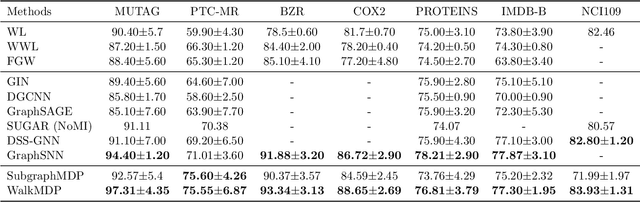
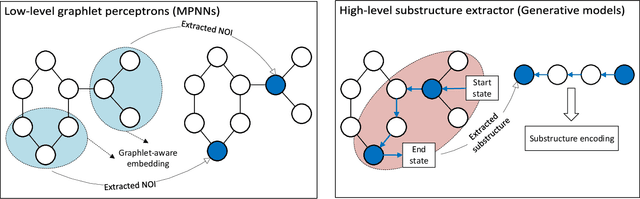
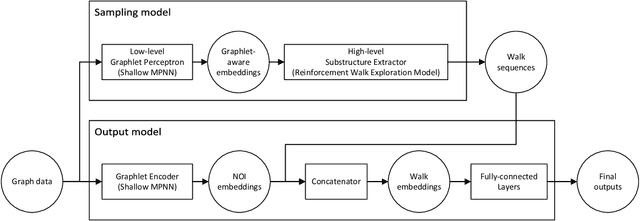
Abstract:Graph data, with its structurally variable nature, represents complex real-world phenomena like chemical compounds, protein structures, and social networks. Traditional Graph Neural Networks (GNNs) primarily utilize the message-passing mechanism, but their expressive power is limited and their prediction lacks explainability. To address these limitations, researchers have focused on graph substructures. Subgraph neural networks (SGNNs) and GNN explainers have emerged as potential solutions, but each has its limitations. SGNNs computes graph representations based on the bags of subgraphs to enhance the expressive power. However, they often rely on predefined algorithm-based sampling strategies, which is inefficient. GNN explainers adopt data-driven approaches to generate important subgraphs to provide explanation. Nevertheless, their explanation is difficult to be translated into practical improvements on GNNs. To overcome these issues, we propose a novel self-supervised framework that integrates SGNNs with the generation approach of GNN explainers, named the Reinforcement Walk Exploration SGNN (RWE-SGNN). Our approach features a sampling model trained in an explainer fashion, optimizing subgraphs to enhance model performance. To achieve a data-driven sampling approach, unlike traditional subgraph generation approaches, we propose a novel walk exploration process, which efficiently extracts important substructures, simplifying the embedding process and avoiding isomorphism problems. Moreover, we prove that our proposed walk exploration process has equivalent generation capability to the traditional subgraph generation process. Experimental results on various graph datasets validate the effectiveness of our proposed method, demonstrating significant improvements in performance and precision.
Anchor Space Optimal Transport: Accelerating Batch Processing of Multiple OT Problems
Oct 24, 2023



Abstract:The optimal transport (OT) theory provides an effective way to compare probability distributions on a defined metric space, but it suffers from cubic computational complexity. Although the Sinkhorn's algorithm greatly reduces the computational complexity of OT solutions, the solutions of multiple OT problems are still time-consuming and memory-comsuming in practice. However, many works on the computational acceleration of OT are usually based on the premise of a single OT problem, ignoring the potential common characteristics of the distributions in a mini-batch. Therefore, we propose a translated OT problem designated as the anchor space optimal transport (ASOT) problem, which is specially designed for batch processing of multiple OT problem solutions. For the proposed ASOT problem, the distributions will be mapped into a shared anchor point space, which learns the potential common characteristics and thus help accelerate OT batch processing. Based on the proposed ASOT, the Wasserstein distance error to the original OT problem is proven to be bounded by ground cost errors. Building upon this, we propose three methods to learn an anchor space minimizing the distance error, each of which has its application background. Numerical experiments on real-world datasets show that our proposed methods can greatly reduce computational time while maintaining reasonable approximation performance.
Safe Screening for Unbalanced Optimal Transport
Jul 01, 2023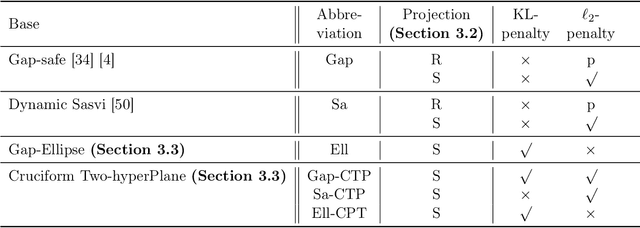
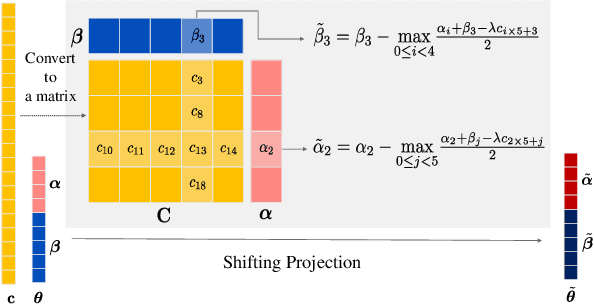

Abstract:This paper introduces a framework that utilizes the Safe Screening technique to accelerate the optimization process of the Unbalanced Optimal Transport (UOT) problem by proactively identifying and eliminating zero elements in the sparse solutions. We demonstrate the feasibility of applying Safe Screening to the UOT problem with $\ell_2$-penalty and KL-penalty by conducting an analysis of the solution's bounds and considering the local strong convexity of the dual problem. Considering the specific structural characteristics of the UOT in comparison to general Lasso problems on the index matrix, we specifically propose a novel approximate projection, an elliptical safe region construction, and a two-hyperplane relaxation method. These enhancements significantly improve the screening efficiency for the UOT's without altering the algorithm's complexity.
Wasserstein Graph Distance based on $L_1$-Approximated Tree Edit Distance between Weisfeiler-Lehman Subtrees
Jul 09, 2022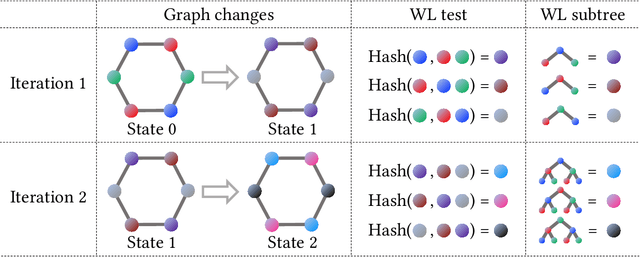
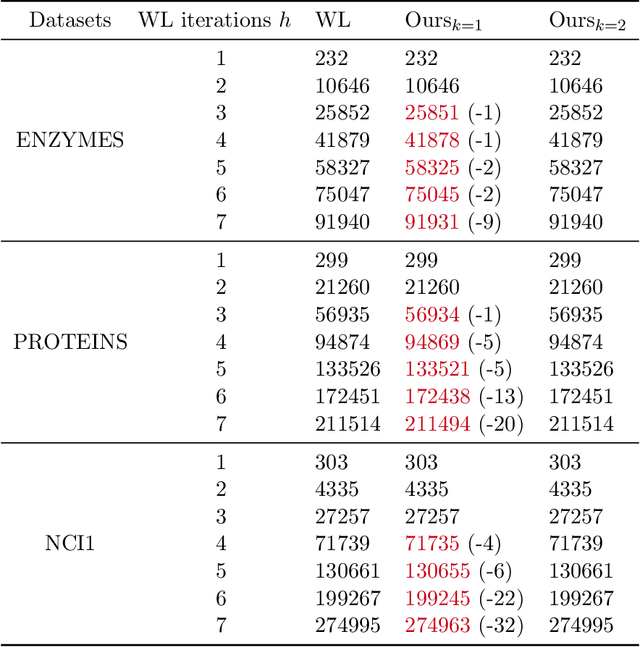
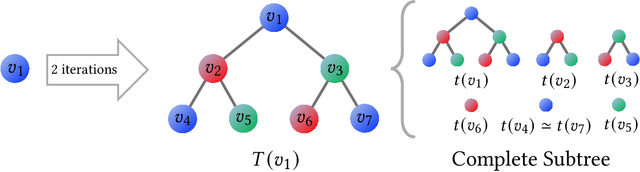
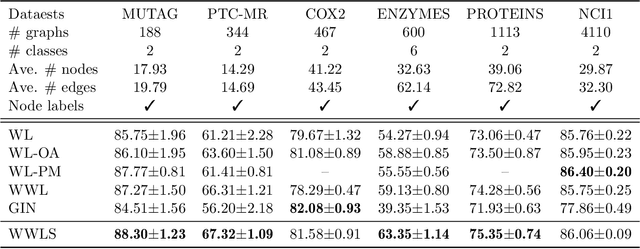
Abstract:The Weisfeiler-Lehman (WL) test has been widely applied to graph kernels, metrics, and neural networks. However, it considers only the graph consistency, resulting in the weak descriptive power of structural information. Thus, it limits the performance improvement of applied methods. In addition, the similarity and distance between graphs defined by the WL test are in coarse measurements. To the best of our knowledge, this paper clarifies these facts for the first time and defines a metric we call the Wasserstein WL subtree (WWLS) distance. We introduce the WL subtree as the structural information in the neighborhood of nodes and assign it to each node. Then we define a new graph embedding space based on $L_1$-approximated tree edit distance ($L_1$-TED): the $L_1$ norm of the difference between node feature vectors on the space is the $L_1$-TED between these nodes. We further propose a fast algorithm for graph embedding. Finally, we use the Wasserstein distance to reflect the $L_1$-TED to the graph level. The WWLS can capture small changes in structure that are difficult with traditional metrics. We demonstrate its performance in several graph classification and metric validation experiments.
On the Convergence of Semi-Relaxed Sinkhorn with Marginal Constraint and OT Distance Gaps
May 27, 2022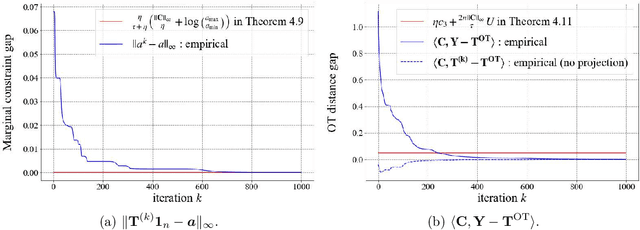
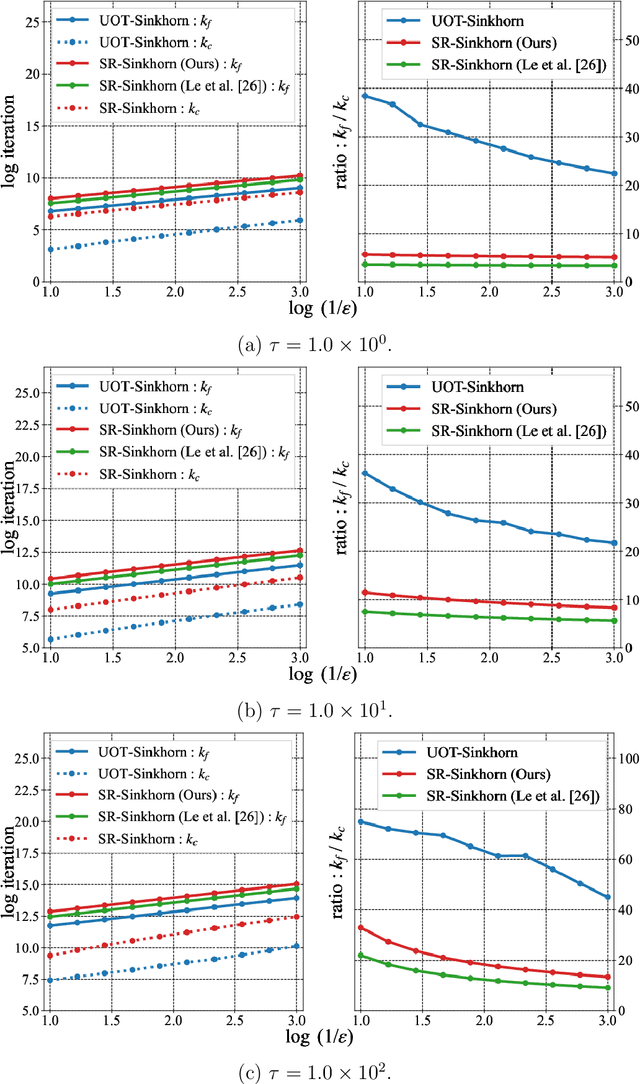
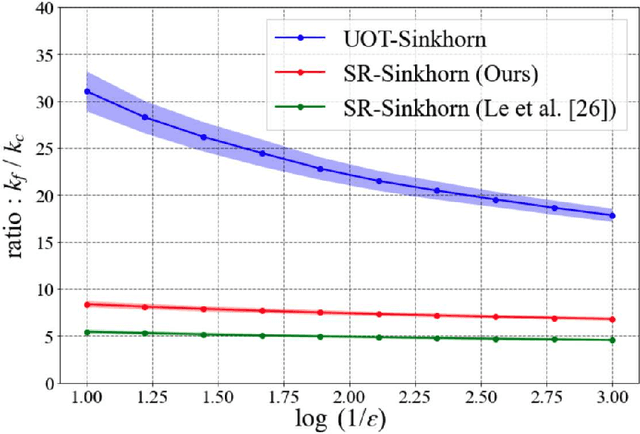
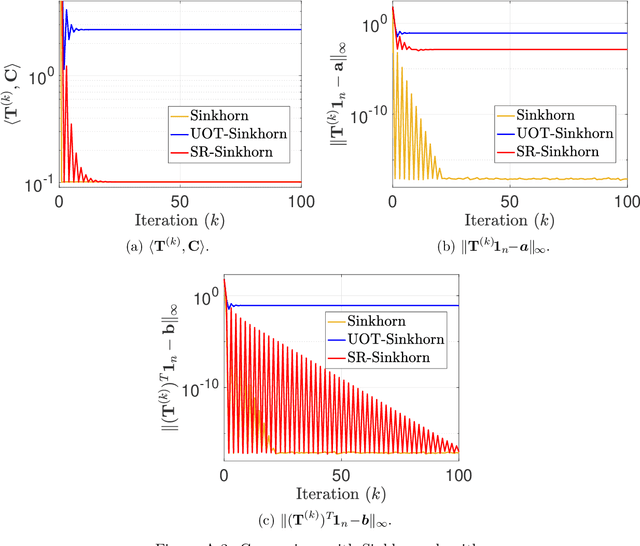
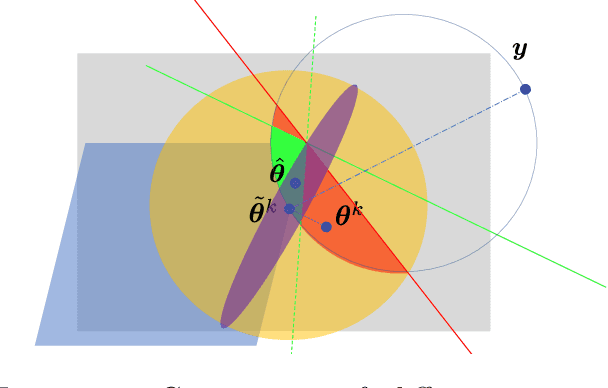
Abstract:This paper presents consideration of the Semi-Relaxed Sinkhorn (SR-Sinkhorn) algorithm for the semi-relaxed optimal transport (SROT) problem, which relaxes one marginal constraint of the standard OT problem. For evaluation of how the constraint relaxation affects the algorithm behavior and solution, it is vitally necessary to present the theoretical convergence analysis in terms not only of the functional value gap, but also of the marginal constraint gap as well as the OT distance gap. However, no existing work has addressed all analyses simultaneously. To this end, this paper presents a comprehensive convergence analysis for SR-Sinkhorn. After presenting the $\epsilon$-approximation of the functional value gap based on a new proof strategy and exploiting this proof strategy, we give the upper bound of the marginal constraint gap. We also provide its convergence to the $\epsilon$-approximation when two distributions are in the probability simplex. Furthermore, the convergence analysis of the OT distance gap to the $\epsilon$-approximation is given as assisted by the obtained marginal constraint gap. The latter two theoretical results are the first results presented in the literature related to the SROT problem.
Block-coordinate Frank-Wolfe algorithm and convergence analysis for semi-relaxed optimal transport problem
May 27, 2022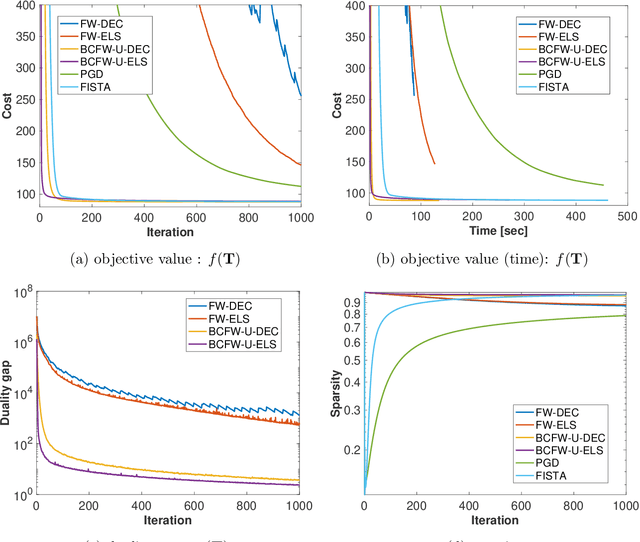
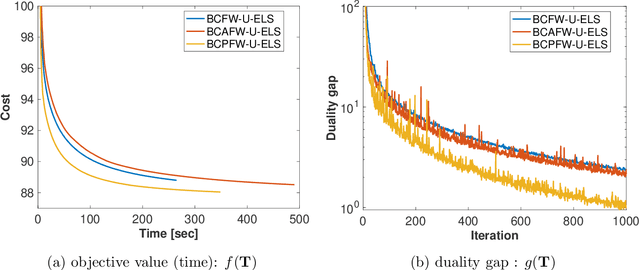
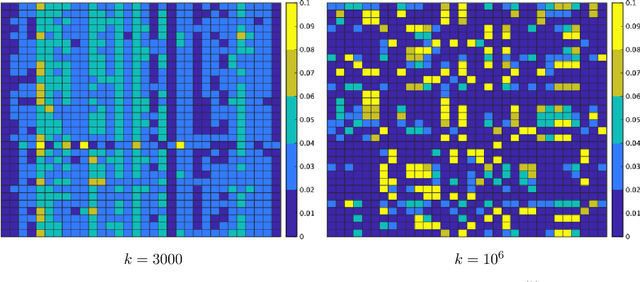
Abstract:The optimal transport (OT) problem has been used widely for machine learning. It is necessary for computation of an OT problem to solve linear programming with tight mass-conservation constraints. These constraints prevent its application to large-scale problems. To address this issue, loosening such constraints enables us to propose the relaxed-OT method using a faster algorithm. This approach has demonstrated its effectiveness for applications. However, it remains slow. As a superior alternative, we propose a fast block-coordinate Frank-Wolfe (BCFW) algorithm for a convex semi-relaxed OT. Specifically, we prove their upper bounds of the worst convergence iterations, and equivalence between the linearization duality gap and the Lagrangian duality gap. Additionally, we develop two fast variants of the proposed BCFW. Numerical experiments have demonstrated that our proposed algorithms are effective for color transfer and surpass state-of-the-art algorithms. This report presents a short version of arXiv:2103.05857.
Fast block-coordinate Frank-Wolfe algorithm for semi-relaxed optimal transport
Mar 10, 2021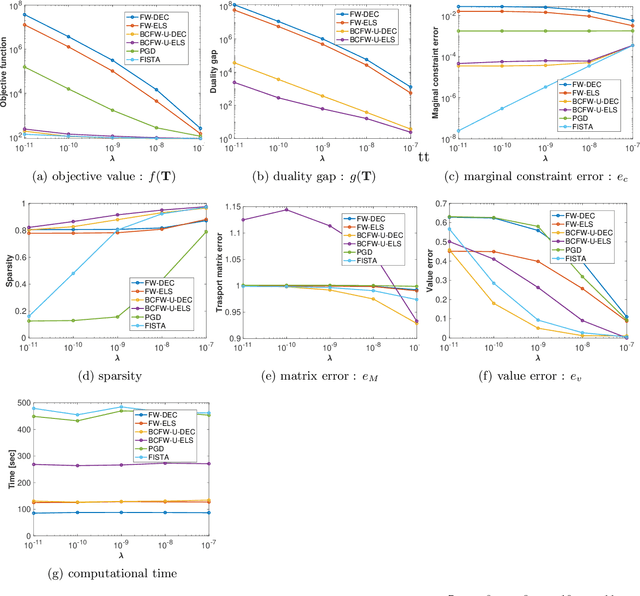
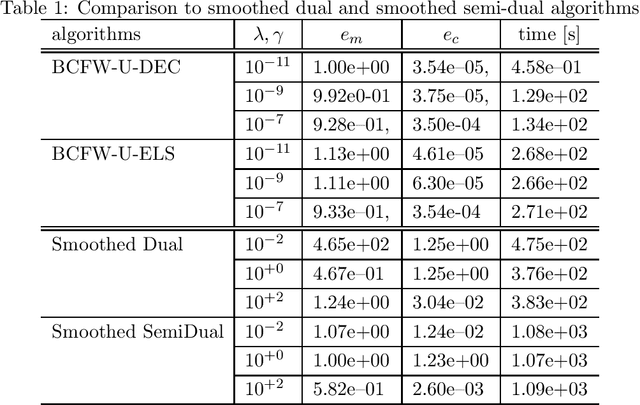
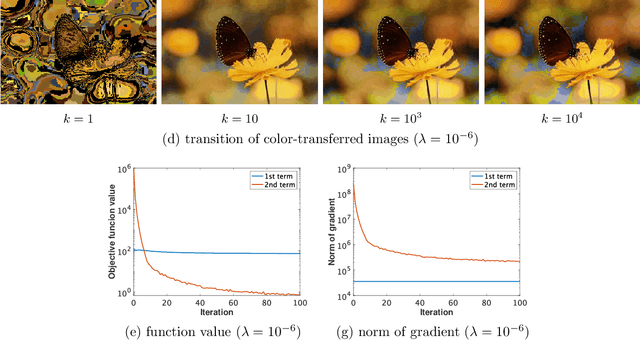
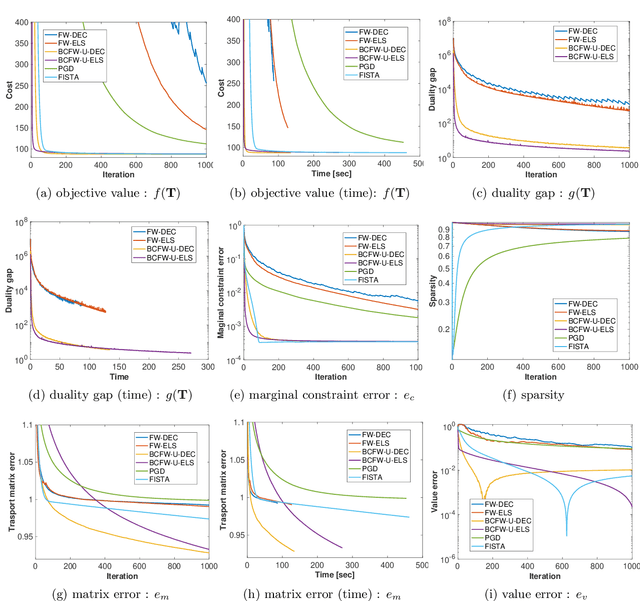
Abstract:Optimal transport (OT), which provides a distance between two probability distributions by considering their spatial locations, has been applied to widely diverse applications. Computing an OT problem requires solution of linear programming with tight mass-conservation constraints. This requirement hinders its application to large-scale problems. To alleviate this issue, the recently proposed relaxed-OT approach uses a faster algorithm by relaxing such constraints. Its effectiveness for practical applications has been demonstrated. Nevertheless, it still exhibits slow convergence. To this end, addressing a convex semi-relaxed OT, we propose a fast block-coordinate Frank-Wolfe (BCFW) algorithm, which gives sparse solutions. Specifically, we provide their upper bounds of the worst convergence iterations, and equivalence between the linearization duality gap and the Lagrangian duality gap. Three fast variants of the proposed BCFW are also proposed. Numerical evaluations in color transfer problem demonstrate that the proposed algorithms outperform state-of-the-art algorithms across different settings.
Manifold optimization for optimal transport
Mar 01, 2021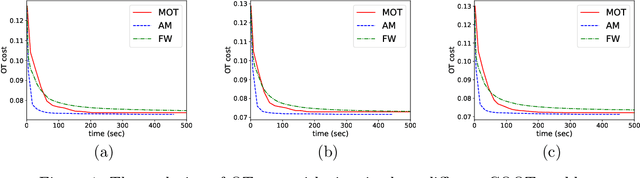
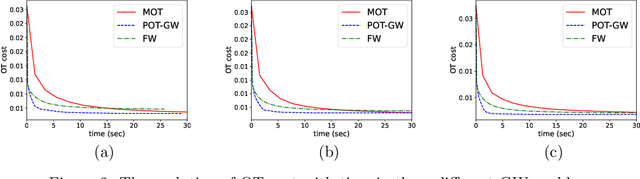
Abstract:Optimal transport (OT) has recently found widespread interest in machine learning. It allows to define novel distances between probability measures, which have shown promise in several applications. In this work, we discuss how to computationally approach OT problems within the framework of the Riemannian manifold optimization. The basis of this is the manifold of doubly stochastic matrices (and its generalization). Even though the manifold geometry is not new, surprisingly, its usefulness for solving OT problems has not been considered. To this end, we specifically discuss optimization-related ingredients that allow modeling the OT problem on smooth Riemannian manifolds by exploiting the geometry of the search space. We also discuss extensions where we reuse the developed optimization ingredients. We make available the Manifold optimization-based Optimal Transport, or MOT, repository with codes useful in solving OT problems in Python and Matlab. The codes are available at https://github.com/SatyadevNtv/MOT.
LCS Graph Kernel Based on Wasserstein Distance in Longest Common Subsequence Metric Space
Dec 07, 2020



Abstract:For graph classification tasks, many methods use a common strategy to aggregate information of vertex neighbors. Although this strategy provides an efficient means of extracting graph topological features, it brings excessive amounts of information that might greatly reduce its accuracy when dealing with large-scale neighborhoods. Learning graphs using paths or walks will not suffer from this difficulty, but many have low utilization of each path or walk, which might engender information loss and high computational costs. To solve this, we propose a graph kernel using a longest common subsequence (LCS kernel) to compute more comprehensive similarity between paths and walks, which resolves substructure isomorphism difficulties. We also combine it with optimal transport theory to extract more in-depth features of graphs. Furthermore, we propose an LCS metric space and apply an adjacent point merge operation to reduce its computational costs. Finally, we demonstrate that our proposed method outperforms many state-of-the-art graph kernel methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge