Fast block-coordinate Frank-Wolfe algorithm for semi-relaxed optimal transport
Paper and Code
Mar 10, 2021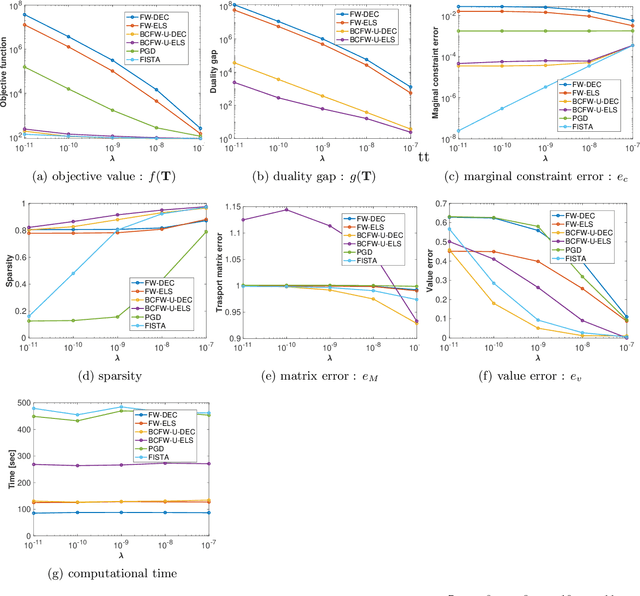
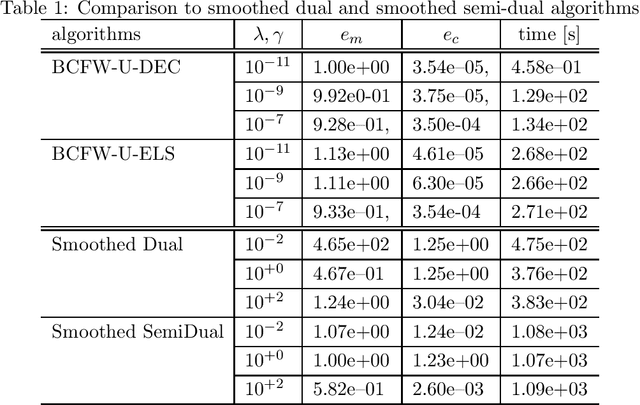
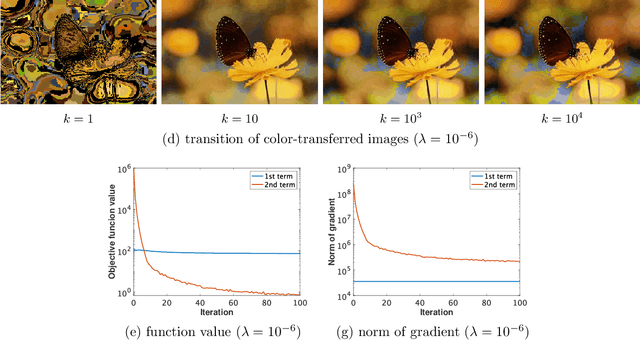
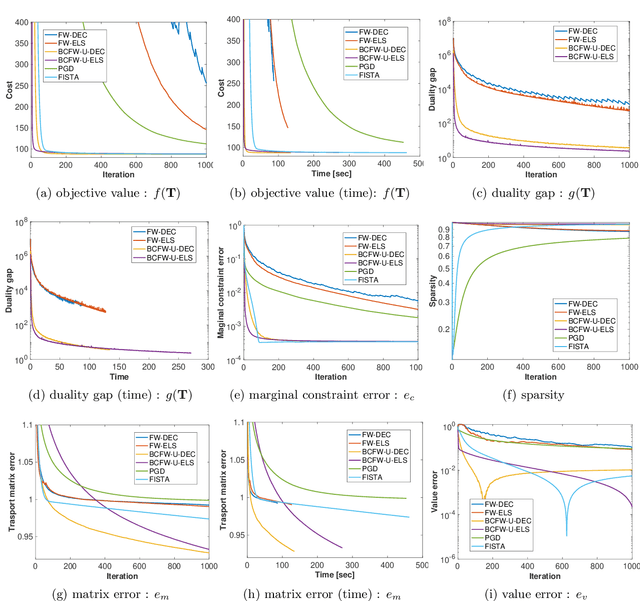
Optimal transport (OT), which provides a distance between two probability distributions by considering their spatial locations, has been applied to widely diverse applications. Computing an OT problem requires solution of linear programming with tight mass-conservation constraints. This requirement hinders its application to large-scale problems. To alleviate this issue, the recently proposed relaxed-OT approach uses a faster algorithm by relaxing such constraints. Its effectiveness for practical applications has been demonstrated. Nevertheless, it still exhibits slow convergence. To this end, addressing a convex semi-relaxed OT, we propose a fast block-coordinate Frank-Wolfe (BCFW) algorithm, which gives sparse solutions. Specifically, we provide their upper bounds of the worst convergence iterations, and equivalence between the linearization duality gap and the Lagrangian duality gap. Three fast variants of the proposed BCFW are also proposed. Numerical evaluations in color transfer problem demonstrate that the proposed algorithms outperform state-of-the-art algorithms across different settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge