On the Convergence of Semi-Relaxed Sinkhorn with Marginal Constraint and OT Distance Gaps

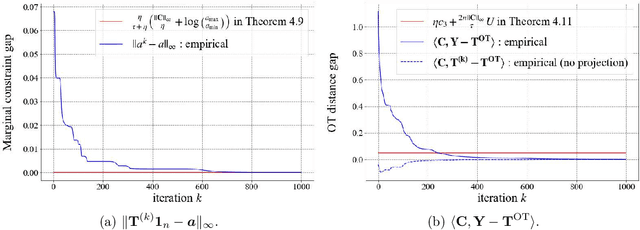
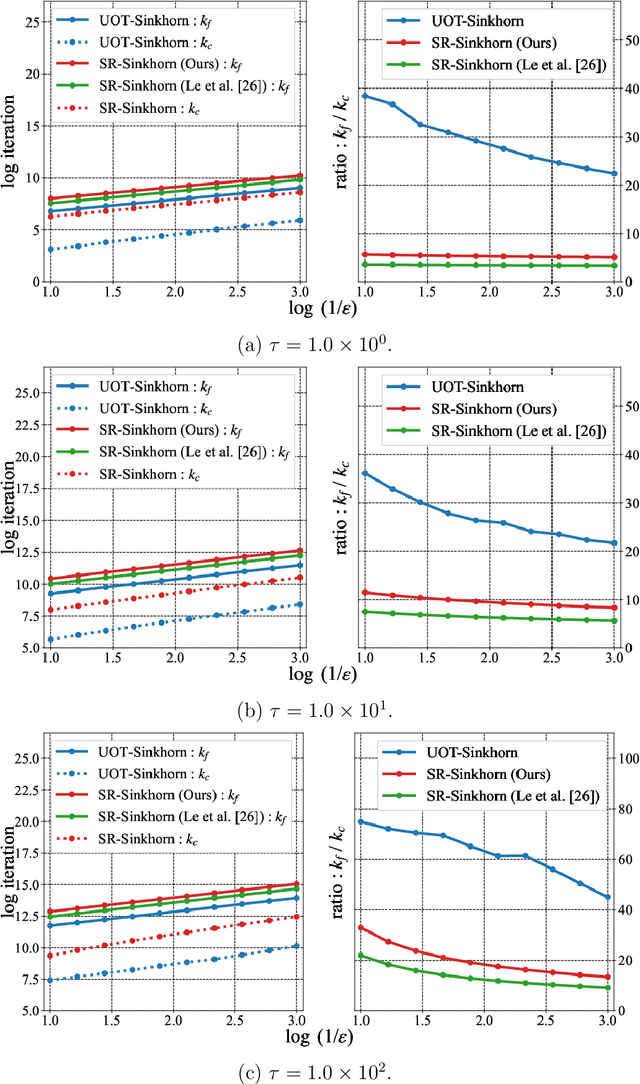
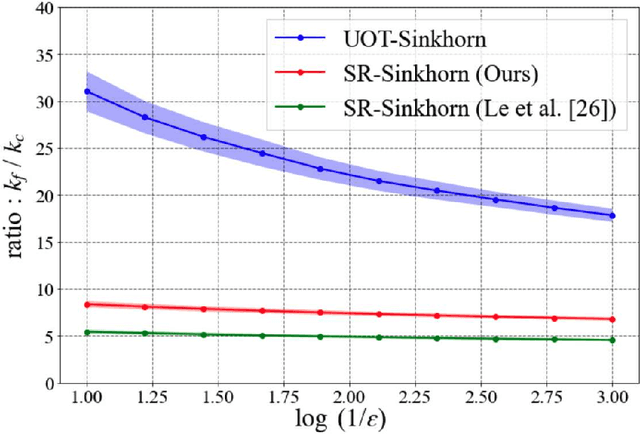
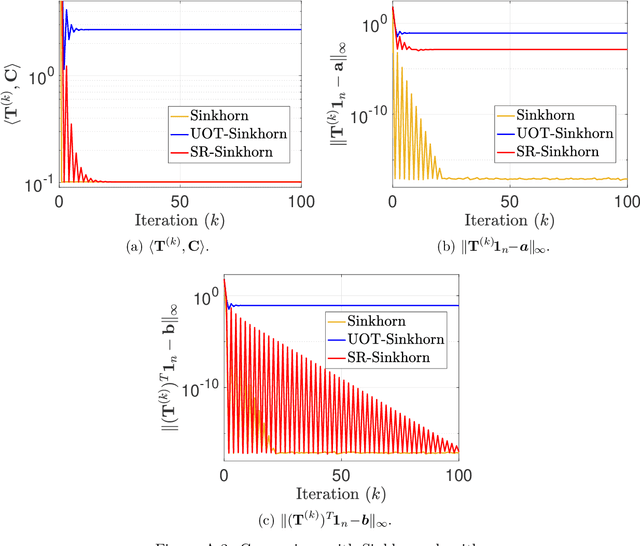
This paper presents consideration of the Semi-Relaxed Sinkhorn (SR-Sinkhorn) algorithm for the semi-relaxed optimal transport (SROT) problem, which relaxes one marginal constraint of the standard OT problem. For evaluation of how the constraint relaxation affects the algorithm behavior and solution, it is vitally necessary to present the theoretical convergence analysis in terms not only of the functional value gap, but also of the marginal constraint gap as well as the OT distance gap. However, no existing work has addressed all analyses simultaneously. To this end, this paper presents a comprehensive convergence analysis for SR-Sinkhorn. After presenting the $\epsilon$-approximation of the functional value gap based on a new proof strategy and exploiting this proof strategy, we give the upper bound of the marginal constraint gap. We also provide its convergence to the $\epsilon$-approximation when two distributions are in the probability simplex. Furthermore, the convergence analysis of the OT distance gap to the $\epsilon$-approximation is given as assisted by the obtained marginal constraint gap. The latter two theoretical results are the first results presented in the literature related to the SROT problem.

Block-coordinate Frank-Wolfe algorithm and convergence analysis for semi-relaxed optimal transport problem

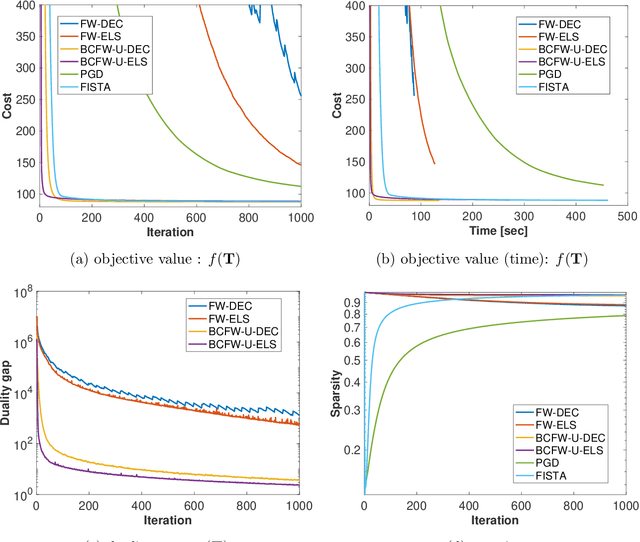
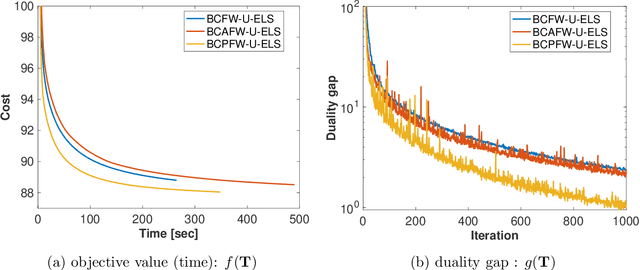
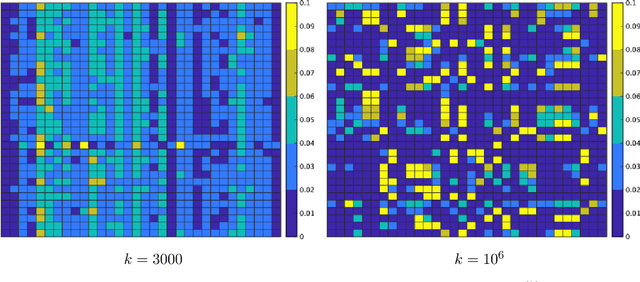
The optimal transport (OT) problem has been used widely for machine learning. It is necessary for computation of an OT problem to solve linear programming with tight mass-conservation constraints. These constraints prevent its application to large-scale problems. To address this issue, loosening such constraints enables us to propose the relaxed-OT method using a faster algorithm. This approach has demonstrated its effectiveness for applications. However, it remains slow. As a superior alternative, we propose a fast block-coordinate Frank-Wolfe (BCFW) algorithm for a convex semi-relaxed OT. Specifically, we prove their upper bounds of the worst convergence iterations, and equivalence between the linearization duality gap and the Lagrangian duality gap. Additionally, we develop two fast variants of the proposed BCFW. Numerical experiments have demonstrated that our proposed algorithms are effective for color transfer and surpass state-of-the-art algorithms. This report presents a short version of arXiv:2103.05857.

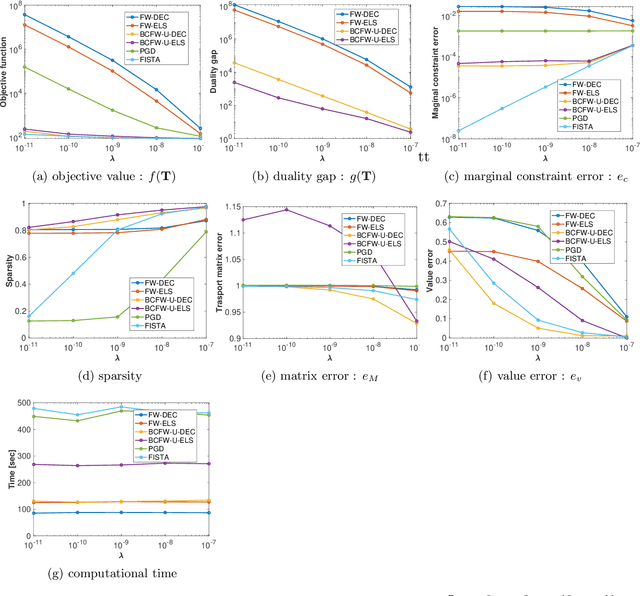
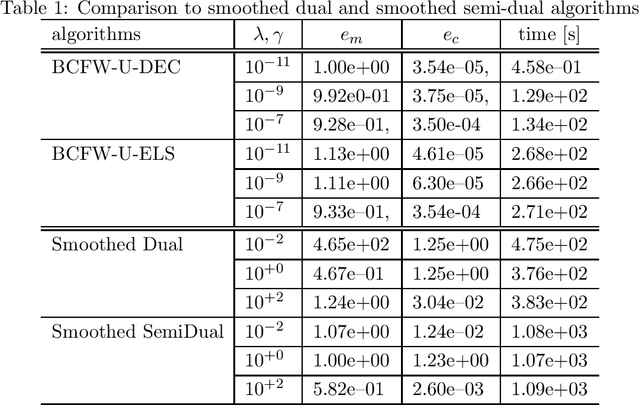
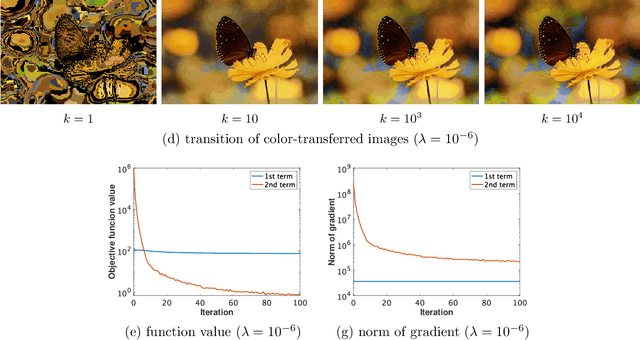
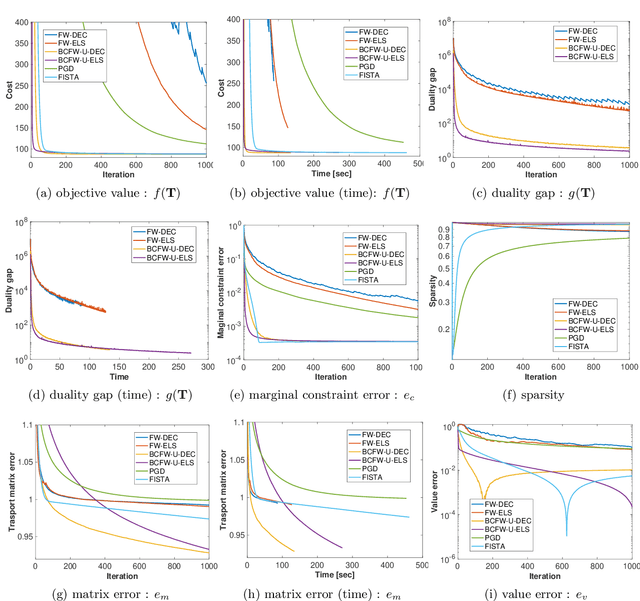
Fast block-coordinate Frank-Wolfe algorithm for semi-relaxed optimal transport

Optimal transport (OT), which provides a distance between two probability distributions by considering their spatial locations, has been applied to widely diverse applications. Computing an OT problem requires solution of linear programming with tight mass-conservation constraints. This requirement hinders its application to large-scale problems. To alleviate this issue, the recently proposed relaxed-OT approach uses a faster algorithm by relaxing such constraints. Its effectiveness for practical applications has been demonstrated. Nevertheless, it still exhibits slow convergence. To this end, addressing a convex semi-relaxed OT, we propose a fast block-coordinate Frank-Wolfe (BCFW) algorithm, which gives sparse solutions. Specifically, we provide their upper bounds of the worst convergence iterations, and equivalence between the linearization duality gap and the Lagrangian duality gap. Three fast variants of the proposed BCFW are also proposed. Numerical evaluations in color transfer problem demonstrate that the proposed algorithms outperform state-of-the-art algorithms across different settings.

Wasserstein k-means with sparse simplex projection

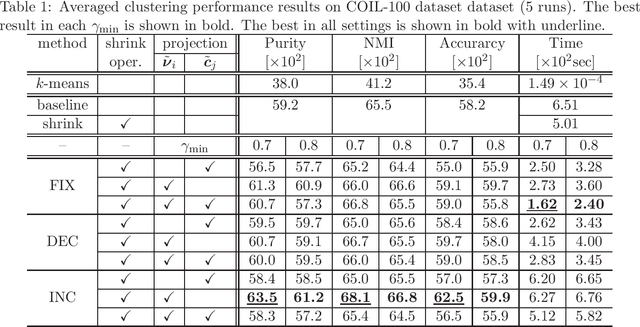
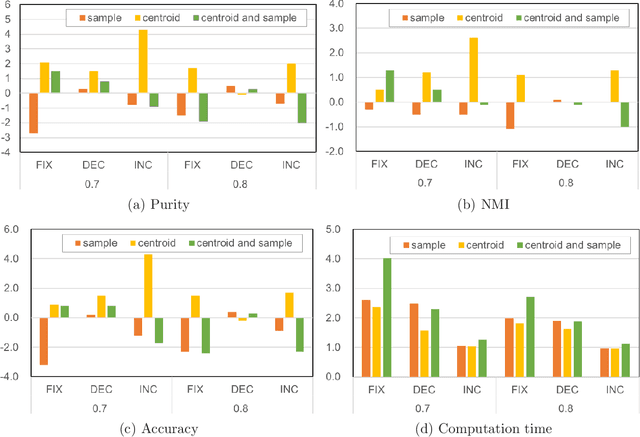
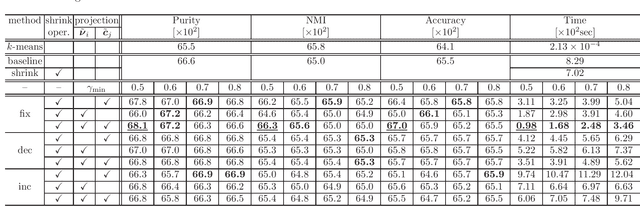
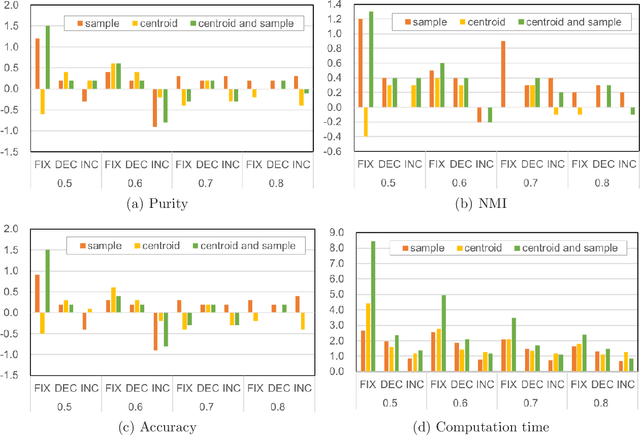
This paper presents a proposal of a faster Wasserstein $k$-means algorithm for histogram data by reducing Wasserstein distance computations and exploiting sparse simplex projection. We shrink data samples, centroids, and the ground cost matrix, which leads to considerable reduction of the computations used to solve optimal transport problems without loss of clustering quality. Furthermore, we dynamically reduced the computational complexity by removing lower-valued data samples and harnessing sparse simplex projection while keeping the degradation of clustering quality lower. We designate this proposed algorithm as sparse simplex projection based Wasserstein $k$-means, or SSPW $k$-means. Numerical evaluations conducted with comparison to results obtained using Wasserstein $k$-means algorithm demonstrate the effectiveness of the proposed SSPW $k$-means for real-world datasets