Manifold optimization for optimal transport

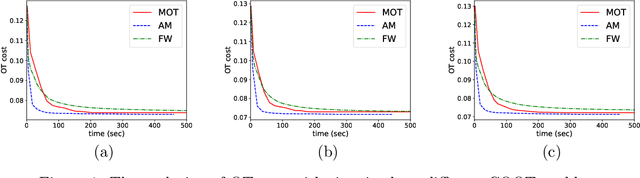
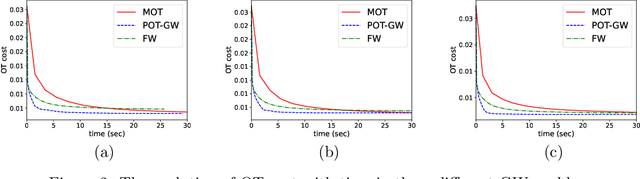
Optimal transport (OT) has recently found widespread interest in machine learning. It allows to define novel distances between probability measures, which have shown promise in several applications. In this work, we discuss how to computationally approach OT problems within the framework of the Riemannian manifold optimization. The basis of this is the manifold of doubly stochastic matrices (and its generalization). Even though the manifold geometry is not new, surprisingly, its usefulness for solving OT problems has not been considered. To this end, we specifically discuss optimization-related ingredients that allow modeling the OT problem on smooth Riemannian manifolds by exploiting the geometry of the search space. We also discuss extensions where we reuse the developed optimization ingredients. We make available the Manifold optimization-based Optimal Transport, or MOT, repository with codes useful in solving OT problems in Python and Matlab. The codes are available at https://github.com/SatyadevNtv/MOT.