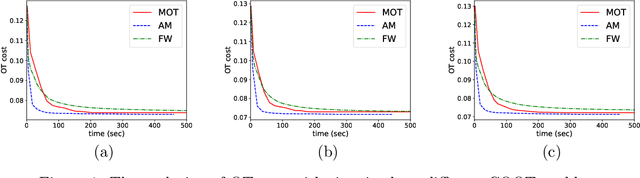
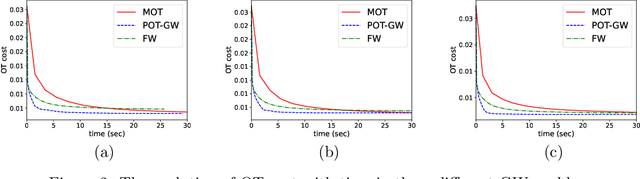
Manifold optimization for optimal transport

Optimal transport (OT) has recently found widespread interest in machine learning. It allows to define novel distances between probability measures, which have shown promise in several applications. In this work, we discuss how to computationally approach OT problems within the framework of the Riemannian manifold optimization. The basis of this is the manifold of doubly stochastic matrices (and its generalization). Even though the manifold geometry is not new, surprisingly, its usefulness for solving OT problems has not been considered. To this end, we specifically discuss optimization-related ingredients that allow modeling the OT problem on smooth Riemannian manifolds by exploiting the geometry of the search space. We also discuss extensions where we reuse the developed optimization ingredients. We make available the Manifold optimization-based Optimal Transport, or MOT, repository with codes useful in solving OT problems in Python and Matlab. The codes are available at https://github.com/SatyadevNtv/MOT.

Efficient robust optimal transport: formulations and algorithms

The problem of robust optimal transport (OT) aims at recovering the best transport plan with respect to the worst possible cost function. In this work, we study novel robust OT formulations where the cost function is parameterized by a symmetric positive semi-definite Mahalanobis metric. In particular, we study several different regularizations on the Mahalanobis metric -- element-wise $p$-norm, KL-divergence, or doubly-stochastic constraint -- and show that the resulting optimization formulations can be considerably simplified by exploiting the problem structure. For large-scale applications, we additionally propose a suitable low-dimensional decomposition of the Mahalanobis metric for the studied robust OT problems. Overall, we view the robust OT (min-max) optimization problems as non-linear OT (minimization) problems, which we solve using a Frank-Wolfe algorithm. We discuss the use of robust OT distance as a loss function in multi-class/multi-label classification problems. Empirical results on several real-world tag prediction and multi-class datasets show the benefit of our modeling approach.

Learning Geometric Word Meta-Embeddings

We propose a geometric framework for learning meta-embeddings of words from different embedding sources. Our framework transforms the embeddings into a common latent space, where, for example, simple averaging of different embeddings (of a given word) is more amenable. The proposed latent space arises from two particular geometric transformations - the orthogonal rotations and the Mahalanobis metric scaling. Empirical results on several word similarity and word analogy benchmarks illustrate the efficacy of the proposed framework.