Anchor Space Optimal Transport: Accelerating Batch Processing of Multiple OT Problems

The optimal transport (OT) theory provides an effective way to compare probability distributions on a defined metric space, but it suffers from cubic computational complexity. Although the Sinkhorn's algorithm greatly reduces the computational complexity of OT solutions, the solutions of multiple OT problems are still time-consuming and memory-comsuming in practice. However, many works on the computational acceleration of OT are usually based on the premise of a single OT problem, ignoring the potential common characteristics of the distributions in a mini-batch. Therefore, we propose a translated OT problem designated as the anchor space optimal transport (ASOT) problem, which is specially designed for batch processing of multiple OT problem solutions. For the proposed ASOT problem, the distributions will be mapped into a shared anchor point space, which learns the potential common characteristics and thus help accelerate OT batch processing. Based on the proposed ASOT, the Wasserstein distance error to the original OT problem is proven to be bounded by ground cost errors. Building upon this, we propose three methods to learn an anchor space minimizing the distance error, each of which has its application background. Numerical experiments on real-world datasets show that our proposed methods can greatly reduce computational time while maintaining reasonable approximation performance.

Safe Screening for Unbalanced Optimal Transport

This paper introduces a framework that utilizes the Safe Screening technique to accelerate the optimization process of the Unbalanced Optimal Transport (UOT) problem by proactively identifying and eliminating zero elements in the sparse solutions. We demonstrate the feasibility of applying Safe Screening to the UOT problem with $\ell_2$-penalty and KL-penalty by conducting an analysis of the solution's bounds and considering the local strong convexity of the dual problem. Considering the specific structural characteristics of the UOT in comparison to general Lasso problems on the index matrix, we specifically propose a novel approximate projection, an elliptical safe region construction, and a two-hyperplane relaxation method. These enhancements significantly improve the screening efficiency for the UOT's without altering the algorithm's complexity.

Wasserstein Graph Distance based on $L_1$-Approximated Tree Edit Distance between Weisfeiler-Lehman Subtrees

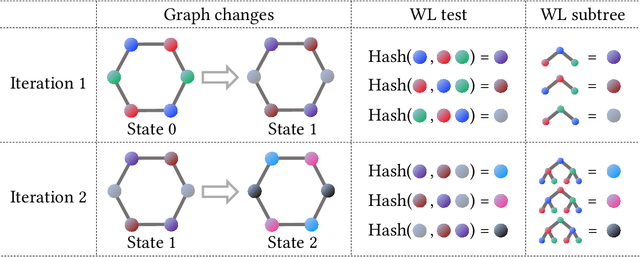
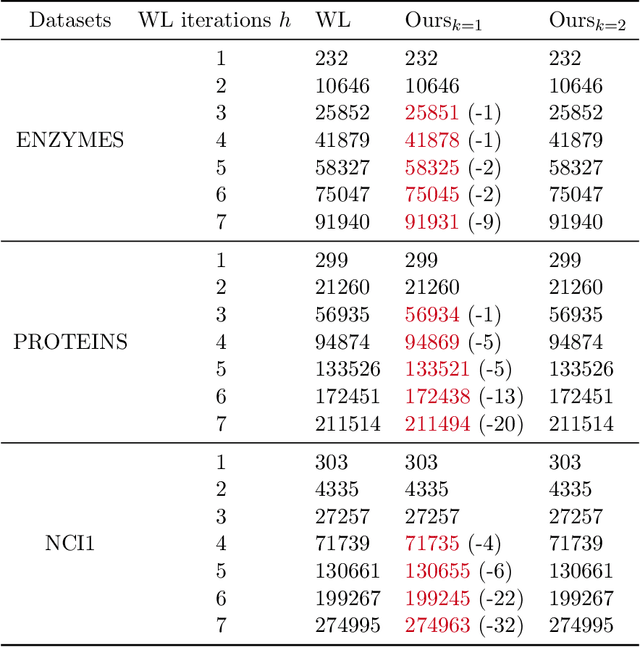
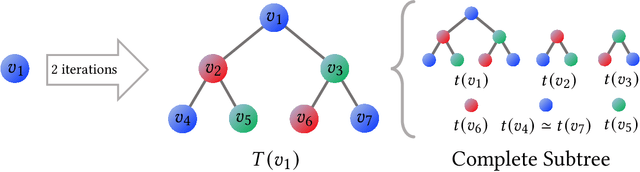
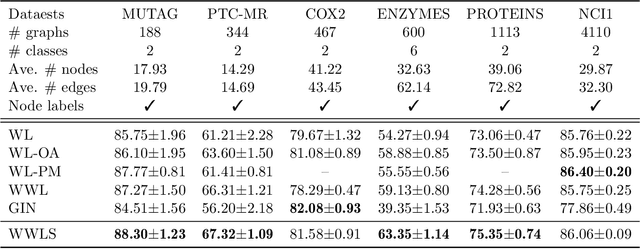
The Weisfeiler-Lehman (WL) test has been widely applied to graph kernels, metrics, and neural networks. However, it considers only the graph consistency, resulting in the weak descriptive power of structural information. Thus, it limits the performance improvement of applied methods. In addition, the similarity and distance between graphs defined by the WL test are in coarse measurements. To the best of our knowledge, this paper clarifies these facts for the first time and defines a metric we call the Wasserstein WL subtree (WWLS) distance. We introduce the WL subtree as the structural information in the neighborhood of nodes and assign it to each node. Then we define a new graph embedding space based on $L_1$-approximated tree edit distance ($L_1$-TED): the $L_1$ norm of the difference between node feature vectors on the space is the $L_1$-TED between these nodes. We further propose a fast algorithm for graph embedding. Finally, we use the Wasserstein distance to reflect the $L_1$-TED to the graph level. The WWLS can capture small changes in structure that are difficult with traditional metrics. We demonstrate its performance in several graph classification and metric validation experiments.

LCS Graph Kernel Based on Wasserstein Distance in Longest Common Subsequence Metric Space

For graph classification tasks, many methods use a common strategy to aggregate information of vertex neighbors. Although this strategy provides an efficient means of extracting graph topological features, it brings excessive amounts of information that might greatly reduce its accuracy when dealing with large-scale neighborhoods. Learning graphs using paths or walks will not suffer from this difficulty, but many have low utilization of each path or walk, which might engender information loss and high computational costs. To solve this, we propose a graph kernel using a longest common subsequence (LCS kernel) to compute more comprehensive similarity between paths and walks, which resolves substructure isomorphism difficulties. We also combine it with optimal transport theory to extract more in-depth features of graphs. Furthermore, we propose an LCS metric space and apply an adjacent point merge operation to reduce its computational costs. Finally, we demonstrate that our proposed method outperforms many state-of-the-art graph kernel methods.