Wasserstein Graph Distance based on $L_1$-Approximated Tree Edit Distance between Weisfeiler-Lehman Subtrees

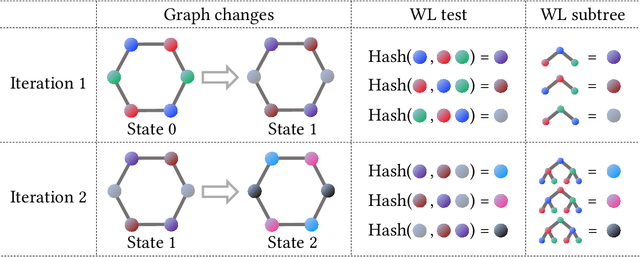
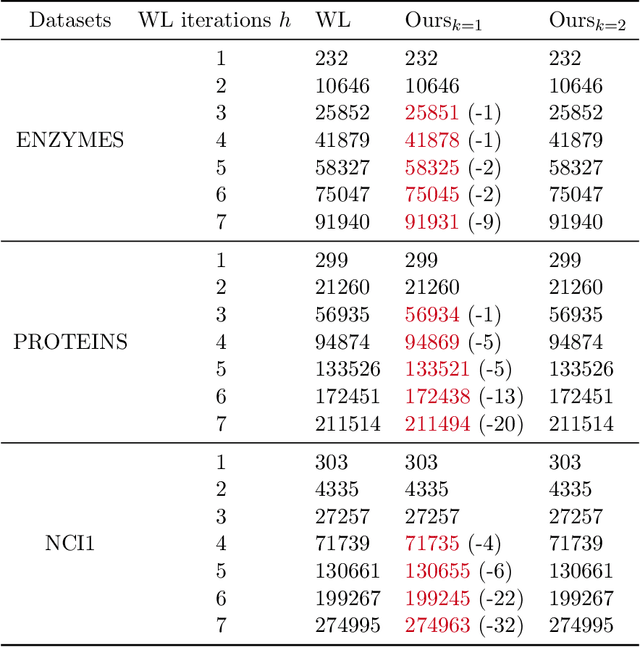
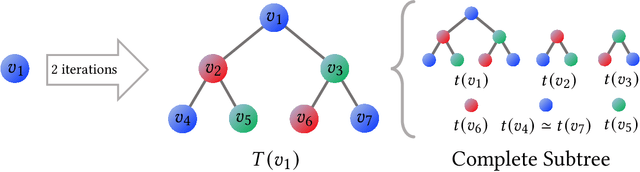
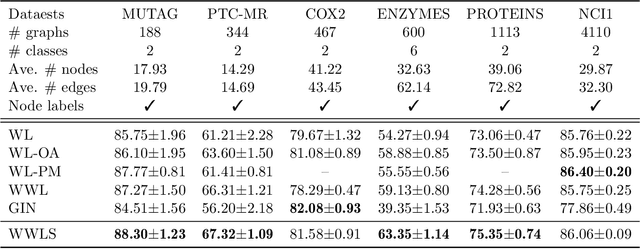
The Weisfeiler-Lehman (WL) test has been widely applied to graph kernels, metrics, and neural networks. However, it considers only the graph consistency, resulting in the weak descriptive power of structural information. Thus, it limits the performance improvement of applied methods. In addition, the similarity and distance between graphs defined by the WL test are in coarse measurements. To the best of our knowledge, this paper clarifies these facts for the first time and defines a metric we call the Wasserstein WL subtree (WWLS) distance. We introduce the WL subtree as the structural information in the neighborhood of nodes and assign it to each node. Then we define a new graph embedding space based on $L_1$-approximated tree edit distance ($L_1$-TED): the $L_1$ norm of the difference between node feature vectors on the space is the $L_1$-TED between these nodes. We further propose a fast algorithm for graph embedding. Finally, we use the Wasserstein distance to reflect the $L_1$-TED to the graph level. The WWLS can capture small changes in structure that are difficult with traditional metrics. We demonstrate its performance in several graph classification and metric validation experiments.