BI-EqNO: Generalized Approximate Bayesian Inference with an Equivariant Neural Operator Framework

Bayesian inference offers a robust framework for updating prior beliefs based on new data using Bayes' theorem, but exact inference is often computationally infeasible, necessitating approximate methods. Though widely used, these methods struggle to estimate marginal likelihoods accurately, particularly due to the rigid functional structures of deterministic models like Gaussian processes and the limitations of small sample sizes in stochastic models like the ensemble Kalman method. In this work, we introduce BI-EqNO, an equivariant neural operator framework for generalized approximate Bayesian inference, designed to enhance both deterministic and stochastic approaches. BI-EqNO transforms priors into posteriors conditioned on observation data through data-driven training. The framework is flexible, supporting diverse prior and posterior representations with arbitrary discretizations and varying numbers of observations. Crucially, BI-EqNO's architecture ensures (1) permutation equivariance between prior and posterior representations, and (2) permutation invariance with respect to observational data. We demonstrate BI-EqNO's utility through two examples: (1) as a generalized Gaussian process (gGP) for regression, and (2) as an ensemble neural filter (EnNF) for sequential data assimilation. Results show that gGP outperforms traditional Gaussian processes by offering a more flexible representation of covariance functions. Additionally, EnNF not only outperforms the ensemble Kalman filter in small-ensemble settings but also has the potential to function as a "super" ensemble filter, capable of representing and integrating multiple ensemble filters for enhanced assimilation performance. This study highlights BI-EqNO's versatility and effectiveness, improving Bayesian inference through data-driven training while reducing computational costs across various applications.

Superresolution Reconstruction of Single Image for Latent features

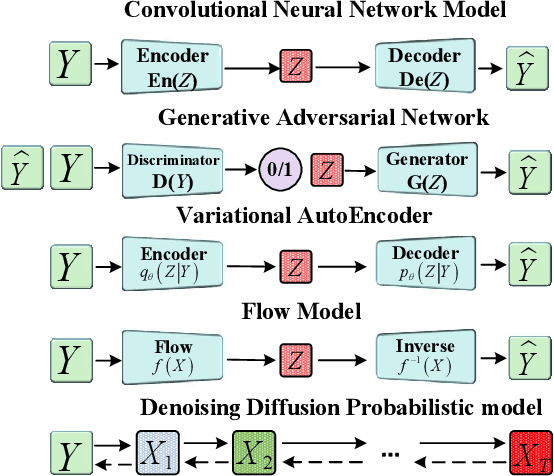
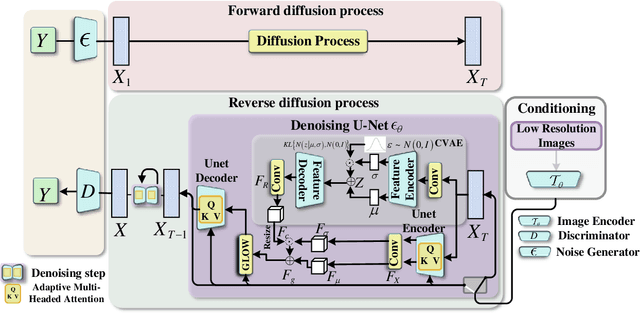
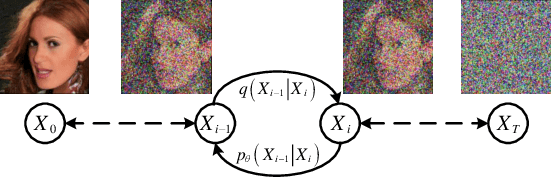
In recent years, Deep Learning has shown good results in the Single Image Superresolution Reconstruction (SISR) task, thus becoming the most widely used methods in this field. The SISR task is a typical task to solve an uncertainty problem. Therefore, it is often challenging to meet the requirements of High-quality sampling, fast Sampling, and diversity of details and texture after Sampling simultaneously in a SISR task.It leads to model collapse, lack of details and texture features after Sampling, and too long Sampling time in High Resolution (HR) image reconstruction methods. This paper proposes a Diffusion Probability model for Latent features (LDDPM) to solve these problems. Firstly, a Conditional Encoder is designed to effectively encode Low-Resolution (LR) images, thereby reducing the solution space of reconstructed images to improve the performance of reconstructed images. Then, the Normalized Flow and Multi-modal adversarial training are used to model the denoising distribution with complex Multi-modal distribution so that the Generative Modeling ability of the model can be improved with a small number of Sampling steps. Experimental results on mainstream datasets demonstrate that our proposed model reconstructs more realistic HR images and obtains better PSNR and SSIM performance compared to existing SISR tasks, thus providing a new idea for SISR tasks.

Frame invariance and scalability of neural operators for partial differential equations

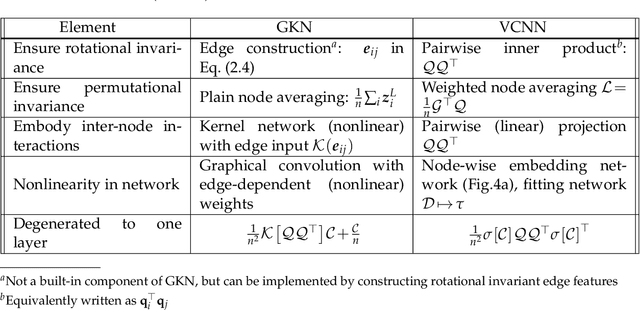
Partial differential equations (PDEs) play a dominant role in the mathematical modeling of many complex dynamical processes. Solving these PDEs often requires prohibitively high computational costs, especially when multiple evaluations must be made for different parameters or conditions. After training, neural operators can provide PDEs solutions significantly faster than traditional PDE solvers. In this work, invariance properties and computational complexity of two neural operators are examined for transport PDE of a scalar quantity. Neural operator based on graph kernel network (GKN) operates on graph-structured data to incorporate nonlocal dependencies. Here we propose a modified formulation of GKN to achieve frame invariance. Vector cloud neural network (VCNN) is an alternate neural operator with embedded frame invariance which operates on point cloud data. GKN-based neural operator demonstrates slightly better predictive performance compared to VCNN. However, GKN requires an excessively high computational cost that increases quadratically with the increasing number of discretized objects as compared to a linear increase for VCNN.

Frame-independent vector-cloud neural network for nonlocal constitutive modelling on arbitrary grids

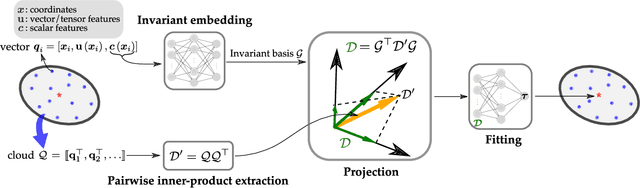
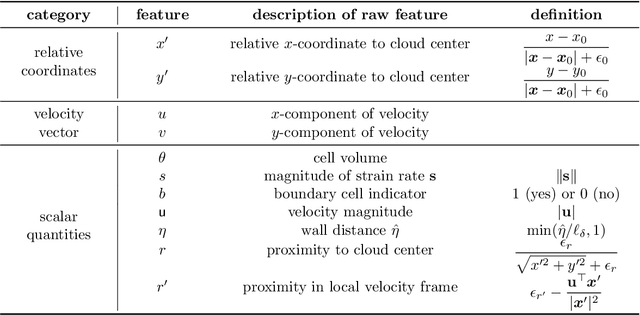
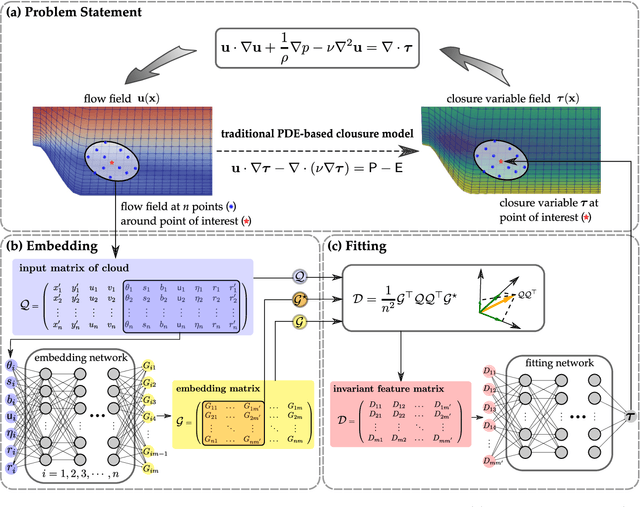
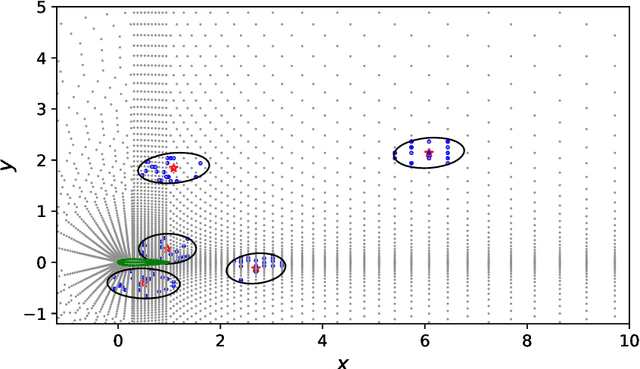
Constitutive models are widely used for modelling complex systems in science and engineering, where first-principle-based, well-resolved simulations are often prohibitively expensive. For example, in fluid dynamics, constitutive models are required to describe nonlocal, unresolved physics such as turbulence and laminar-turbulent transition. In particular, Reynolds stress models for turbulence and intermittency transport equations for laminar-turbulent transition both utilize convection--diffusion partial differential equations (PDEs). However, traditional PDE-based constitutive models can lack robustness and are often too rigid to accommodate diverse calibration data. We propose a frame-independent, nonlocal constitutive model based on a vector-cloud neural network that can be trained with data. The learned constitutive model can predict the closure variable at a point based on the flow information in its neighborhood. Such nonlocal information is represented by a group of points, each having a feature vector attached to it, and thus the input is referred to as vector cloud. The cloud is mapped to the closure variable through a frame-independent neural network, which is invariant both to coordinate translation and rotation and to the ordering of points in the cloud. As such, the network takes any number of arbitrarily arranged grid points as input and thus is suitable for unstructured meshes commonly used in fluid flow simulations. The merits of the proposed network are demonstrated on scalar transport PDEs on a family of parameterized periodic hill geometries. Numerical results show that the vector-cloud neural network is a promising tool not only as nonlocal constitutive models and but also as general surrogate models for PDEs on irregular domains.

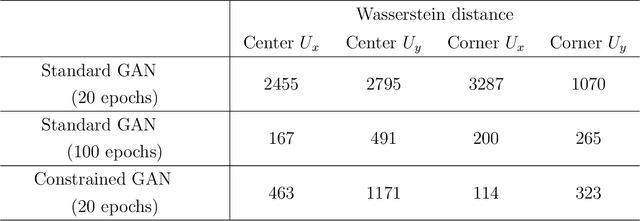
Enforcing Deterministic Constraints on Generative Adversarial Networks for Emulating Physical Systems

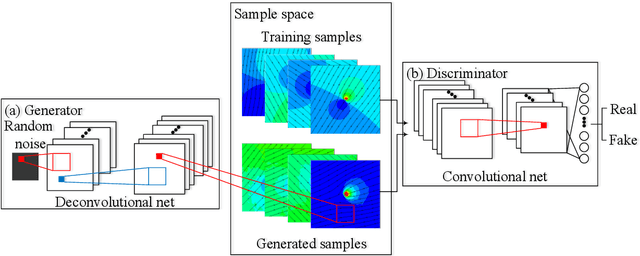
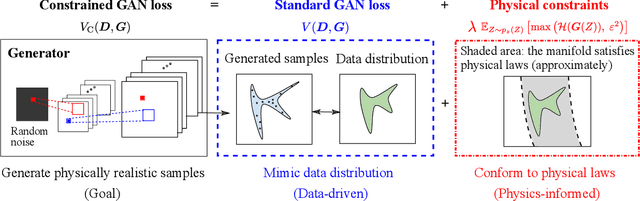
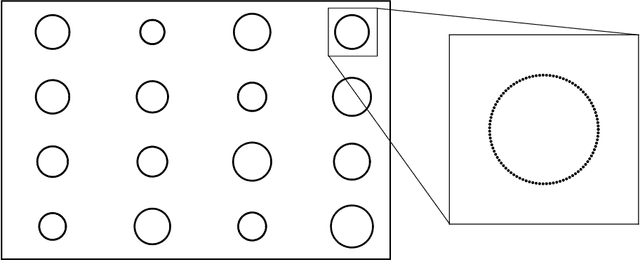
Generative adversarial networks (GANs) are initially proposed to generate images by learning from a large number of samples. Recently, GANs have been used to emulate complex physical systems such as turbulent flows. However, a critical question must be answered before GANs can be considered trusted emulators for physical systems: do GANs-generated samples conform to the various physical constraints? These include both deterministic constraints (e.g., conservation laws) and statistical constraints (e.g., energy spectrum in turbulent flows). The latter has been studied in a companion paper (Wu et al. 2019. Enforcing statistical constraints in generative adversarial networks for modeling chaotic dynamical systems. arxiv:1905.06841). In the present work, we enforce deterministic yet approximate constraints on GANs by incorporating them into the loss function of the generator. We evaluate the performance of physics-constrained GANs on two representative tasks with geometrical constraints (generating points on circles) and differential constraints (generating divergence-free flow velocity fields), respectively. In both cases, the constrained GANs produced samples that precisely conform to the underlying constraints, even though the constraints are only enforced approximately. More importantly, the imposed constraints significantly accelerate the convergence and improve the robustness in the training. These improvements are noteworthy, as the convergence and robustness are two well-known obstacles in the training of GANs.

Enforcing Statistical Constraints in Generative Adversarial Networks for Modeling Chaotic Dynamical Systems

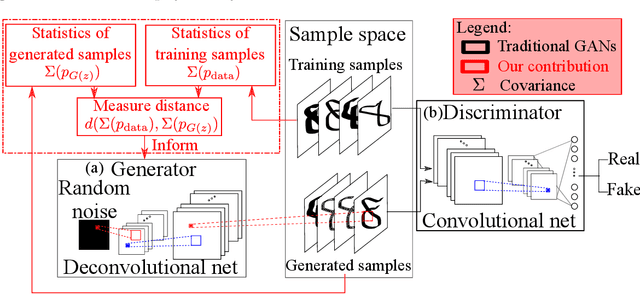
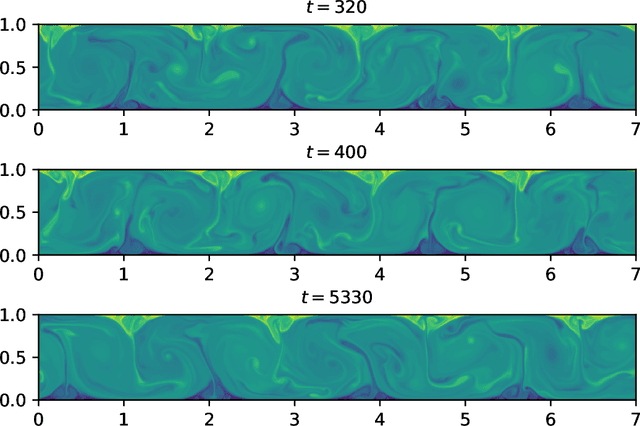
Simulating complex physical systems often involves solving partial differential equations (PDEs) with some closures due to the presence of multi-scale physics that cannot be fully resolved. Therefore, reliable and accurate closure models for unresolved physics remains an important requirement for many computational physics problems, e.g., turbulence simulation. Recently, several researchers have adopted generative adversarial networks (GANs), a novel paradigm of training machine learning models, to generate solutions of PDEs-governed complex systems without having to numerically solve these PDEs. However, GANs are known to be difficult in training and likely to converge to local minima, where the generated samples do not capture the true statistics of the training data. In this work, we present a statistical constrained generative adversarial network by enforcing constraints of covariance from the training data, which results in an improved machine-learning-based emulator to capture the statistics of the training data generated by solving fully resolved PDEs. We show that such a statistical regularization leads to better performance compared to standard GANs, measured by (1) the constrained model's ability to more faithfully emulate certain physical properties of the system and (2) the significantly reduced (by up to 80%) training time to reach the solution. We exemplify this approach on the Rayleigh-Benard convection, a turbulent flow system that is an idealized model of the Earth's atmosphere. With the growth of high-fidelity simulation databases of physical systems, this work suggests great potential for being an alternative to the explicit modeling of closures or parameterizations for unresolved physics, which are known to be a major source of uncertainty in simulating multi-scale physical systems, e.g., turbulence or Earth's climate.

Prediction of Reynolds Stresses in High-Mach-Number Turbulent Boundary Layers using Physics-Informed Machine Learning

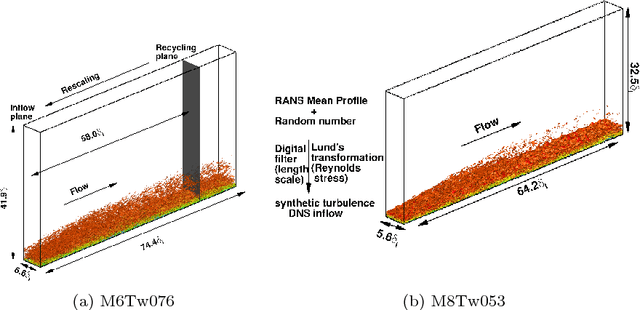
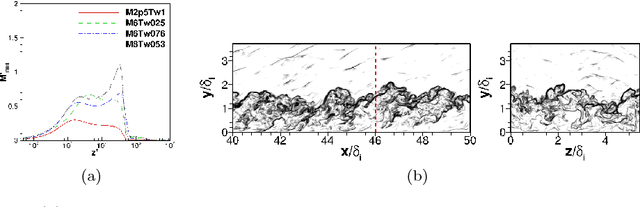
Modeled Reynolds stress is a major source of model-form uncertainties in Reynolds-averaged Navier-Stokes (RANS) simulations. Recently, a physics-informed machine-learning (PIML) approach has been proposed for reconstructing the discrepancies in RANS-modeled Reynolds stresses. The merits of the PIML framework has been demonstrated in several canonical incompressible flows. However, its performance on high-Mach-number flows is still not clear. In this work we use the PIML approach to predict the discrepancies in RANS modeled Reynolds stresses in high-Mach-number flat-plate turbulent boundary layers by using an existing DNS database. Specifically, the discrepancy function is first constructed using a DNS training flow and then used to correct RANS-predicted Reynolds stresses under flow conditions different from the DNS. The machine-learning technique is shown to significantly improve RANS-modeled turbulent normal stresses, the turbulent kinetic energy, and the Reynolds-stress anisotropy. Improvements are consistently observed when different training datasets are used. Moreover, a high-dimensional visualization technique and distance metrics are used to provide a priori assessment of prediction confidence based only on RANS simulations. This study demonstrates that the PIML approach is a computationally affordable technique for improving the accuracy of RANS-modeled Reynolds stresses for high-Mach-number turbulent flows when there is a lack of experiments and high-fidelity simulations.