Muhammad I. Zafar
Frame invariance and scalability of neural operators for partial differential equations
Dec 28, 2021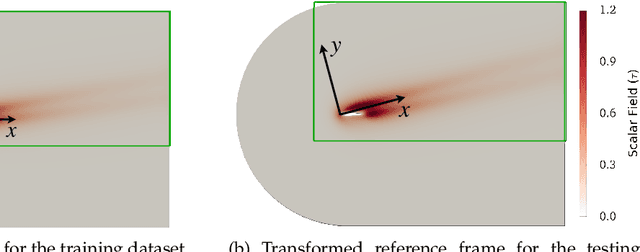
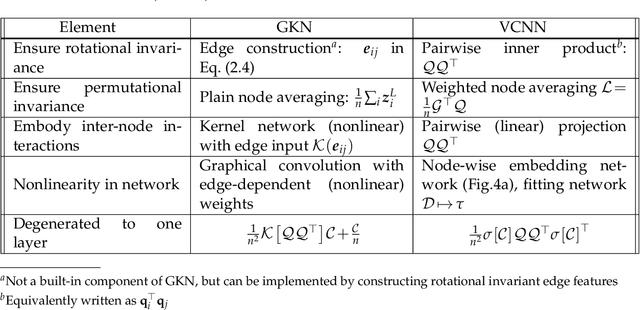
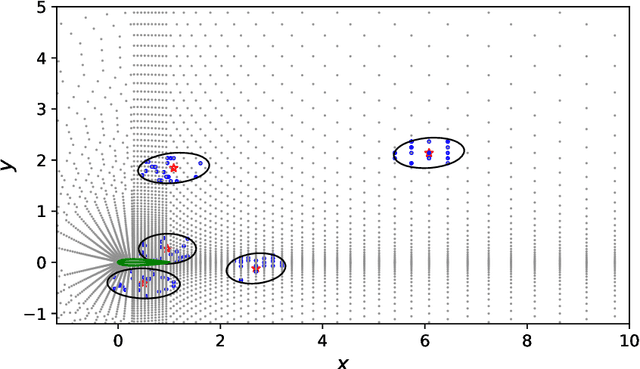

Abstract:Partial differential equations (PDEs) play a dominant role in the mathematical modeling of many complex dynamical processes. Solving these PDEs often requires prohibitively high computational costs, especially when multiple evaluations must be made for different parameters or conditions. After training, neural operators can provide PDEs solutions significantly faster than traditional PDE solvers. In this work, invariance properties and computational complexity of two neural operators are examined for transport PDE of a scalar quantity. Neural operator based on graph kernel network (GKN) operates on graph-structured data to incorporate nonlocal dependencies. Here we propose a modified formulation of GKN to achieve frame invariance. Vector cloud neural network (VCNN) is an alternate neural operator with embedded frame invariance which operates on point cloud data. GKN-based neural operator demonstrates slightly better predictive performance compared to VCNN. However, GKN requires an excessively high computational cost that increases quadratically with the increasing number of discretized objects as compared to a linear increase for VCNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge