Xu-Hui Zhou
BI-EqNO: Generalized Approximate Bayesian Inference with an Equivariant Neural Operator Framework
Oct 21, 2024Abstract:Bayesian inference offers a robust framework for updating prior beliefs based on new data using Bayes' theorem, but exact inference is often computationally infeasible, necessitating approximate methods. Though widely used, these methods struggle to estimate marginal likelihoods accurately, particularly due to the rigid functional structures of deterministic models like Gaussian processes and the limitations of small sample sizes in stochastic models like the ensemble Kalman method. In this work, we introduce BI-EqNO, an equivariant neural operator framework for generalized approximate Bayesian inference, designed to enhance both deterministic and stochastic approaches. BI-EqNO transforms priors into posteriors conditioned on observation data through data-driven training. The framework is flexible, supporting diverse prior and posterior representations with arbitrary discretizations and varying numbers of observations. Crucially, BI-EqNO's architecture ensures (1) permutation equivariance between prior and posterior representations, and (2) permutation invariance with respect to observational data. We demonstrate BI-EqNO's utility through two examples: (1) as a generalized Gaussian process (gGP) for regression, and (2) as an ensemble neural filter (EnNF) for sequential data assimilation. Results show that gGP outperforms traditional Gaussian processes by offering a more flexible representation of covariance functions. Additionally, EnNF not only outperforms the ensemble Kalman filter in small-ensemble settings but also has the potential to function as a "super" ensemble filter, capable of representing and integrating multiple ensemble filters for enhanced assimilation performance. This study highlights BI-EqNO's versatility and effectiveness, improving Bayesian inference through data-driven training while reducing computational costs across various applications.
Frame invariance and scalability of neural operators for partial differential equations
Dec 28, 2021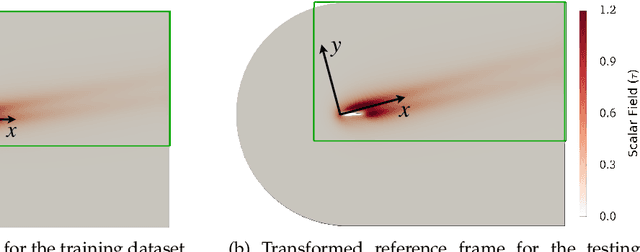
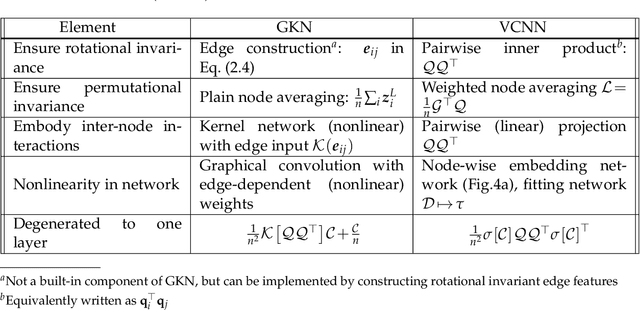

Abstract:Partial differential equations (PDEs) play a dominant role in the mathematical modeling of many complex dynamical processes. Solving these PDEs often requires prohibitively high computational costs, especially when multiple evaluations must be made for different parameters or conditions. After training, neural operators can provide PDEs solutions significantly faster than traditional PDE solvers. In this work, invariance properties and computational complexity of two neural operators are examined for transport PDE of a scalar quantity. Neural operator based on graph kernel network (GKN) operates on graph-structured data to incorporate nonlocal dependencies. Here we propose a modified formulation of GKN to achieve frame invariance. Vector cloud neural network (VCNN) is an alternate neural operator with embedded frame invariance which operates on point cloud data. GKN-based neural operator demonstrates slightly better predictive performance compared to VCNN. However, GKN requires an excessively high computational cost that increases quadratically with the increasing number of discretized objects as compared to a linear increase for VCNN.
Frame-independent vector-cloud neural network for nonlocal constitutive modelling on arbitrary grids
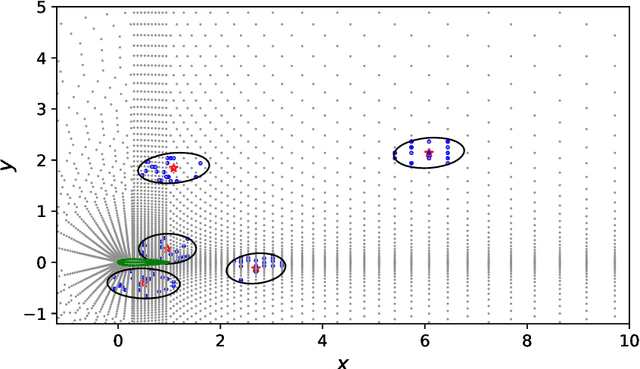
Mar 11, 2021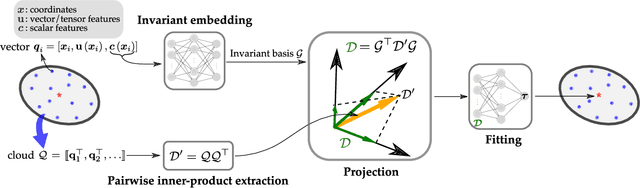
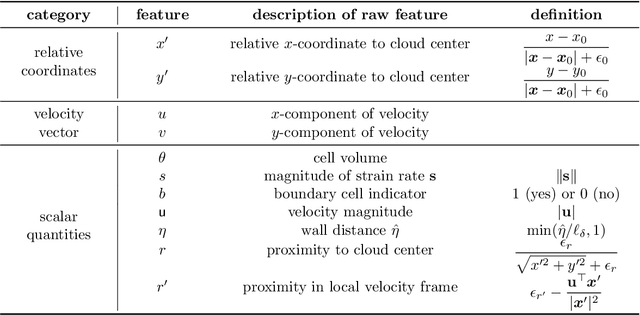
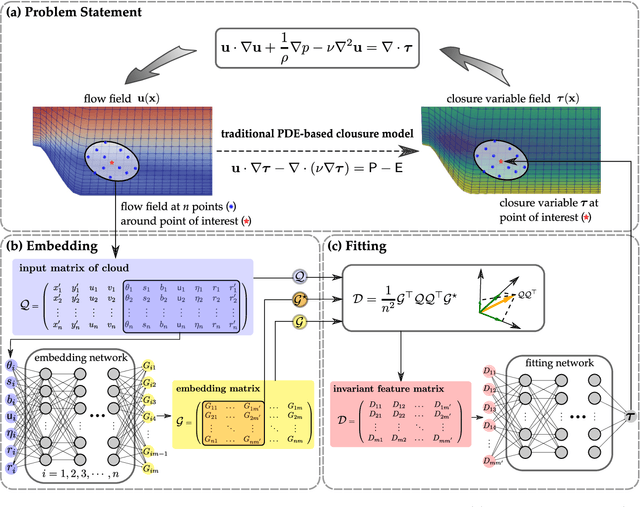

Abstract:Constitutive models are widely used for modelling complex systems in science and engineering, where first-principle-based, well-resolved simulations are often prohibitively expensive. For example, in fluid dynamics, constitutive models are required to describe nonlocal, unresolved physics such as turbulence and laminar-turbulent transition. In particular, Reynolds stress models for turbulence and intermittency transport equations for laminar-turbulent transition both utilize convection--diffusion partial differential equations (PDEs). However, traditional PDE-based constitutive models can lack robustness and are often too rigid to accommodate diverse calibration data. We propose a frame-independent, nonlocal constitutive model based on a vector-cloud neural network that can be trained with data. The learned constitutive model can predict the closure variable at a point based on the flow information in its neighborhood. Such nonlocal information is represented by a group of points, each having a feature vector attached to it, and thus the input is referred to as vector cloud. The cloud is mapped to the closure variable through a frame-independent neural network, which is invariant both to coordinate translation and rotation and to the ordering of points in the cloud. As such, the network takes any number of arbitrarily arranged grid points as input and thus is suitable for unstructured meshes commonly used in fluid flow simulations. The merits of the proposed network are demonstrated on scalar transport PDEs on a family of parameterized periodic hill geometries. Numerical results show that the vector-cloud neural network is a promising tool not only as nonlocal constitutive models and but also as general surrogate models for PDEs on irregular domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge