ReLU-KAN: New Kolmogorov-Arnold Networks that Only Need Matrix Addition, Dot Multiplication, and ReLU

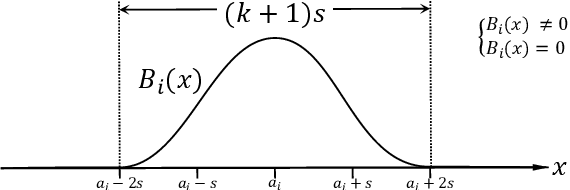
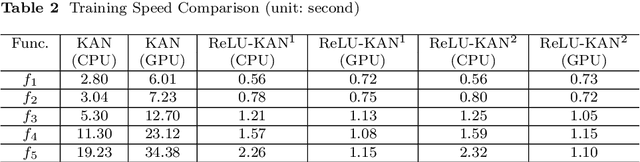
Limited by the complexity of basis function (B-spline) calculations, Kolmogorov-Arnold Networks (KAN) suffer from restricted parallel computing capability on GPUs. This paper proposes a novel ReLU-KAN implementation that inherits the core idea of KAN. By adopting ReLU (Rectified Linear Unit) and point-wise multiplication, we simplify the design of KAN's basis function and optimize the computation process for efficient CUDA computing. The proposed ReLU-KAN architecture can be readily implemented on existing deep learning frameworks (e.g., PyTorch) for both inference and training. Experimental results demonstrate that ReLU-KAN achieves a 20x speedup compared to traditional KAN with 4-layer networks. Furthermore, ReLU-KAN exhibits a more stable training process with superior fitting ability while preserving the "catastrophic forgetting avoidance" property of KAN. You can get the code in https://github.com/quiqi/relu_kan

On the uncertainty analysis of the data-enabled physics-informed neural network for solving neutron diffusion eigenvalue problem

In practical engineering experiments, the data obtained through detectors are inevitably noisy. For the already proposed data-enabled physics-informed neural network (DEPINN) \citep{DEPINN}, we investigate the performance of DEPINN in calculating the neutron diffusion eigenvalue problem from several perspectives when the prior data contain different scales of noise. Further, in order to reduce the effect of noise and improve the utilization of the noisy prior data, we propose innovative interval loss functions and give some rigorous mathematical proofs. The robustness of DEPINN is examined on two typical benchmark problems through a large number of numerical results, and the effectiveness of the proposed interval loss function is demonstrated by comparison. This paper confirms the feasibility of the improved DEPINN for practical engineering applications in nuclear reactor physics.