Minder: Faulty Machine Detection for Large-scale Distributed Model Training

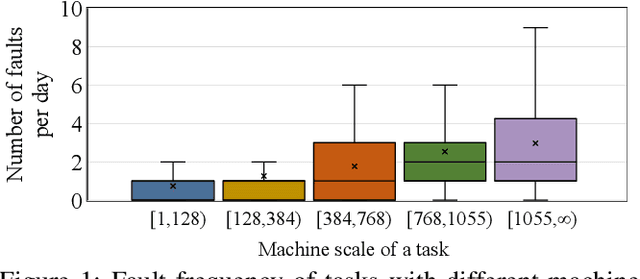
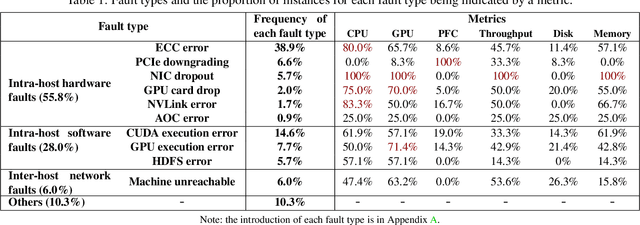
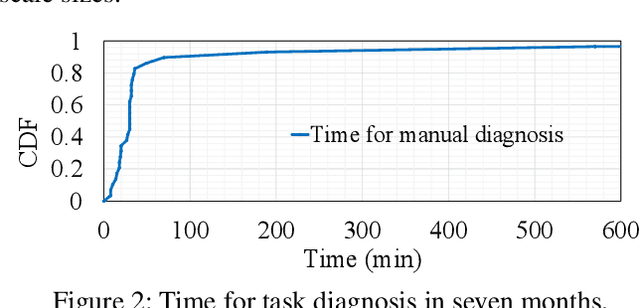
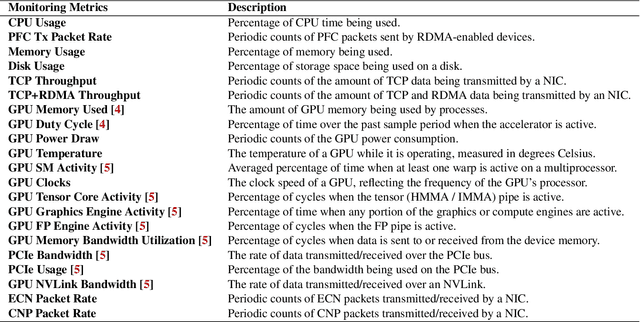
Large-scale distributed model training requires simultaneous training on up to thousands of machines. Faulty machine detection is critical when an unexpected fault occurs in a machine. From our experience, a training task can encounter two faults per day on average, possibly leading to a halt for hours. To address the drawbacks of the time-consuming and labor-intensive manual scrutiny, we propose Minder, an automatic faulty machine detector for distributed training tasks. The key idea of Minder is to automatically and efficiently detect faulty distinctive monitoring metric patterns, which could last for a period before the entire training task comes to a halt. Minder has been deployed in our production environment for over one year, monitoring daily distributed training tasks where each involves up to thousands of machines. In our real-world fault detection scenarios, Minder can accurately and efficiently react to faults within 3.6 seconds on average, with a precision of 0.904 and F1-score of 0.893.

MMPDE-Net and Moving Sampling Physics-informed Neural Networks Based On Moving Mesh Method

In this work, we propose an end-to-end adaptive sampling neural network (MMPDE-Net) based on the moving mesh PDE method, which can adaptively generate new coordinates of sampling points by solving the moving mesh PDE. This model focuses on improving the efficiency of individual sampling points. Moreover, we have developed an iterative algorithm based on MMPDE-Net, which makes the sampling points more precise and controllable. Since MMPDE-Net is a framework independent of the deep learning solver, we combine it with PINN to propose MS-PINN and demonstrate its effectiveness by performing error analysis under the assumptions given in this paper. Meanwhile, we demonstrate the performance improvement of MS-PINN compared to PINN through numerical experiments on four typical examples to verify the effectiveness of our method.

On the uncertainty analysis of the data-enabled physics-informed neural network for solving neutron diffusion eigenvalue problem

In practical engineering experiments, the data obtained through detectors are inevitably noisy. For the already proposed data-enabled physics-informed neural network (DEPINN) \citep{DEPINN}, we investigate the performance of DEPINN in calculating the neutron diffusion eigenvalue problem from several perspectives when the prior data contain different scales of noise. Further, in order to reduce the effect of noise and improve the utilization of the noisy prior data, we propose innovative interval loss functions and give some rigorous mathematical proofs. The robustness of DEPINN is examined on two typical benchmark problems through a large number of numerical results, and the effectiveness of the proposed interval loss function is demonstrated by comparison. This paper confirms the feasibility of the improved DEPINN for practical engineering applications in nuclear reactor physics.

Neural Networks Base on Power Method and Inverse Power Method for Solving Linear Eigenvalue Problems

In this article, we propose three methods Power Method Neural Network (PMNN), Inverse Power Method Neural Networ (IPMNN) and Shifted Inverse Power Method Neural Network (SIPMNN) combined with power method, inverse power method and shifted inverse power method to solve eigenvalue problems with the dominant eigenvalue, the smallest eigenvalue and the smallest zero eigenvalue, respectively. The methods share similar spirits with traditional methods, but the differences are the differential operator realized by Automatic Differentiation (AD), the eigenfunction learned by the neural network and the iterations implemented by optimizing the specially defined loss function. We examine the applicability and accuracy of our methods in several numerical examples in high dimensions. Numerical results obtained by our methods for multidimensional problems show that our methods can provide accurate eigenvalue and eigenfunction approximations.