HAR-DoReMi: Optimizing Data Mixture for Self-Supervised Human Activity Recognition Across Heterogeneous IMU Datasets

Cross-dataset Human Activity Recognition (HAR) suffers from limited model generalization, hindering its practical deployment. To address this critical challenge, inspired by the success of DoReMi in Large Language Models (LLMs), we introduce a data mixture optimization strategy for pre-training HAR models, aiming to improve the recognition performance across heterogeneous datasets. However, directly applying DoReMi to the HAR field encounters new challenges due to the continuous, multi-channel and intrinsic heterogeneous characteristics of IMU sensor data. To overcome these limitations, we propose a novel framework HAR-DoReMi, which introduces a masked reconstruction task based on Mean Squared Error (MSE) loss. By raplacing the discrete language sequence prediction task, which relies on the Negative Log-Likelihood (NLL) loss, in the original DoReMi framework, the proposed framework is inherently more appropriate for handling the continuous and multi-channel characteristics of IMU data. In addition, HAR-DoReMi integrates the Mahony fusion algorithm into the self-supervised HAR pre-training, aiming to mitigate the heterogeneity of varying sensor orientation. This is achieved by estimating the sensor orientation within each dataset and facilitating alignment with a unified coordinate system, thereby improving the cross-dataset generalization ability of the HAR model. Experimental evaluation on multiple cross-dataset HAR transfer tasks demonstrates that HAR-DoReMi improves the accuracy by an average of 6.51%, compared to the current state-of-the-art method with only approximately 30% to 50% of the data usage. These results confirm the effectiveness of HAR-DoReMi in improving the generalization and data efficiency of pre-training HAR models, underscoring its significant potential to facilitate the practical deployment of HAR technology.

Reliable Projection Based Unsupervised Learning for Semi-Definite QCQP with Application of Beamforming Optimization

In this paper, we investigate a special class of quadratic-constrained quadratic programming (QCQP) with semi-definite constraints. Traditionally, since such a problem is non-convex and N-hard, the neural network (NN) is regarded as a promising method to obtain a high-performing solution. However, due to the inherent prediction error, it is challenging to ensure all solution output by the NN is feasible. Although some existing methods propose some naive methods, they only focus on reducing the constraint violation probability, where not all solutions are feasibly guaranteed. To deal with the above challenge, in this paper a computing efficient and reliable projection is proposed, where all solution output by the NN are ensured to be feasible. Moreover, unsupervised learning is used, so the NN can be trained effectively and efficiently without labels. Theoretically, the solution of the NN after projection is proven to be feasible, and we also prove the projection method can enhance the convergence performance and speed of the NN. To evaluate our proposed method, the quality of service (QoS)-contained beamforming scenario is studied, where the simulation results show the proposed method can achieve high-performance which is competitive with the lower bound.

Trapezoidal Gradient Descent for Effective Reinforcement Learning in Spiking Networks

With the rapid development of artificial intelligence technology, the field of reinforcement learning has continuously achieved breakthroughs in both theory and practice. However, traditional reinforcement learning algorithms often entail high energy consumption during interactions with the environment. Spiking Neural Network (SNN), with their low energy consumption characteristics and performance comparable to deep neural networks, have garnered widespread attention. To reduce the energy consumption of practical applications of reinforcement learning, researchers have successively proposed the Pop-SAN and MDC-SAN algorithms. Nonetheless, these algorithms use rectangular functions to approximate the spike network during the training process, resulting in low sensitivity, thus indicating room for improvement in the training effectiveness of SNN. Based on this, we propose a trapezoidal approximation gradient method to replace the spike network, which not only preserves the original stable learning state but also enhances the model's adaptability and response sensitivity under various signal dynamics. Simulation results show that the improved algorithm, using the trapezoidal approximation gradient to replace the spike network, achieves better convergence speed and performance compared to the original algorithm and demonstrates good training stability.

ReLU-KAN: New Kolmogorov-Arnold Networks that Only Need Matrix Addition, Dot Multiplication, and ReLU

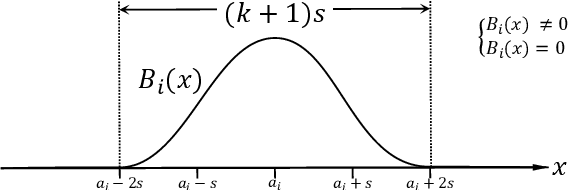
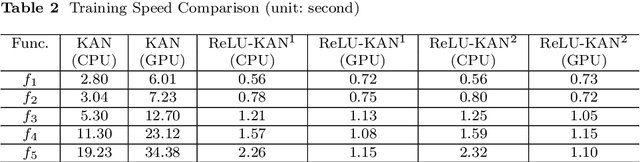
Limited by the complexity of basis function (B-spline) calculations, Kolmogorov-Arnold Networks (KAN) suffer from restricted parallel computing capability on GPUs. This paper proposes a novel ReLU-KAN implementation that inherits the core idea of KAN. By adopting ReLU (Rectified Linear Unit) and point-wise multiplication, we simplify the design of KAN's basis function and optimize the computation process for efficient CUDA computing. The proposed ReLU-KAN architecture can be readily implemented on existing deep learning frameworks (e.g., PyTorch) for both inference and training. Experimental results demonstrate that ReLU-KAN achieves a 20x speedup compared to traditional KAN with 4-layer networks. Furthermore, ReLU-KAN exhibits a more stable training process with superior fitting ability while preserving the "catastrophic forgetting avoidance" property of KAN. You can get the code in https://github.com/quiqi/relu_kan