Enhancing Compositional Generalization via Compositional Feature Alignment

Real-world applications of machine learning models often confront data distribution shifts, wherein discrepancies exist between the training and test data distributions. In the common multi-domain multi-class setup, as the number of classes and domains scales up, it becomes infeasible to gather training data for every domain-class combination. This challenge naturally leads the quest for models with Compositional Generalization (CG) ability, where models can generalize to unseen domain-class combinations. To delve into the CG challenge, we develop CG-Bench, a suite of CG benchmarks derived from existing real-world image datasets, and observe that the prevalent pretraining-finetuning paradigm on foundational models, such as CLIP and DINOv2, struggles with the challenge. To address this challenge, we propose Compositional Feature Alignment (CFA), a simple two-stage finetuning technique that i) learns two orthogonal linear heads on a pretrained encoder with respect to class and domain labels, and ii) fine-tunes the encoder with the newly learned head frozen. We theoretically and empirically justify that CFA encourages compositional feature learning of pretrained models. We further conduct extensive experiments on CG-Bench for CLIP and DINOv2, two powerful pretrained vision foundation models. Experiment results show that CFA outperforms common finetuning techniques in compositional generalization, corroborating CFA's efficacy in compositional feature learning.

Invariant-Feature Subspace Recovery: A New Class of Provable Domain Generalization Algorithms

Domain generalization asks for models trained over a set of training environments to generalize well in unseen test environments. Recently, a series of algorithms such as Invariant Risk Minimization (IRM) have been proposed for domain generalization. However, Rosenfeld et al. (2021) shows that in a simple linear data model, even if non-convexity issues are ignored, IRM and its extensions cannot generalize to unseen environments with less than $d_s+1$ training environments, where $d_s$ is the dimension of the spurious-feature subspace. In this work, we propose Invariant-feature Subspace Recovery (ISR): a new class of algorithms to achieve provable domain generalization across the settings of classification and regression problems. First, in the binary classification setup of Rosenfeld et al. (2021), we show that our first algorithm, ISR-Mean, can identify the subspace spanned by invariant features from the first-order moments of the class-conditional distributions, and achieve provable domain generalization with $d_s+1$ training environments. Our second algorithm, ISR-Cov, further reduces the required number of training environments to $O(1)$ using the information of second-order moments. Notably, unlike IRM, our algorithms bypass non-convexity issues and enjoy global convergence guarantees. Next, we extend ISR-Mean to the more general setting of multi-class classification and propose ISR-Multiclass, which leverages class information and provably recovers the invariant-feature subspace with $\lceil d_s/k\rceil+1$ training environments for $k$-class classification. Finally, for regression problems, we propose ISR-Regression that can identify the invariant-feature subspace with $d_s+1$ training environments. Empirically, we demonstrate the superior performance of our ISRs on synthetic benchmarks. Further, ISR can be used as post-processing methods for feature extractors such as neural nets.

Fully Self-Supervised Depth Estimation from Defocus Clue

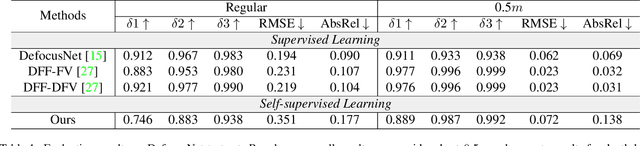
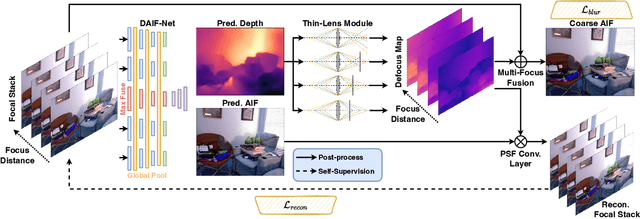
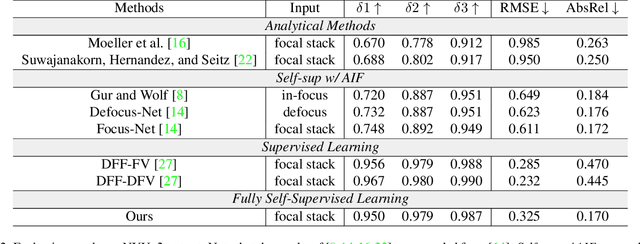
Depth-from-defocus (DFD), modeling the relationship between depth and defocus pattern in images, has demonstrated promising performance in depth estimation. Recently, several self-supervised works try to overcome the difficulties in acquiring accurate depth ground-truth. However, they depend on the all-in-focus (AIF) images, which cannot be captured in real-world scenarios. Such limitation discourages the applications of DFD methods. To tackle this issue, we propose a completely self-supervised framework that estimates depth purely from a sparse focal stack. We show that our framework circumvents the needs for the depth and AIF image ground-truth, and receives superior predictions, thus closing the gap between the theoretical success of DFD works and their applications in the real world. In particular, we propose (i) a more realistic setting for DFD tasks, where no depth or AIF image ground-truth is available; (ii) a novel self-supervision framework that provides reliable predictions of depth and AIF image under the challenging setting. The proposed framework uses a neural model to predict the depth and AIF image, and utilizes an optical model to validate and refine the prediction. We verify our framework on three benchmark datasets with rendered focal stacks and real focal stacks. Qualitative and quantitative evaluations show that our method provides a strong baseline for self-supervised DFD tasks.

Provable Domain Generalization via Invariant-Feature Subspace Recovery

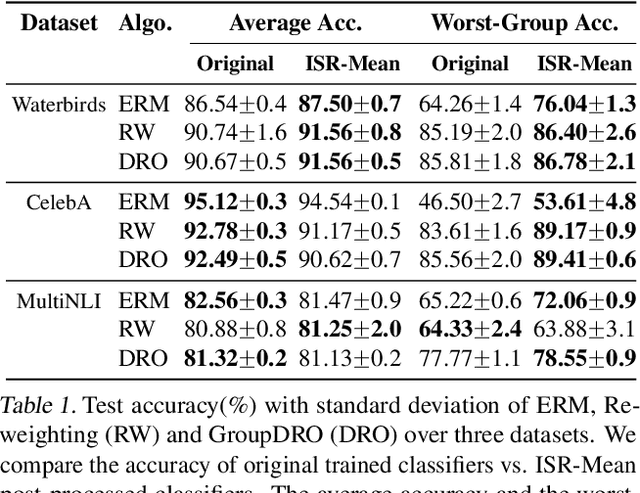
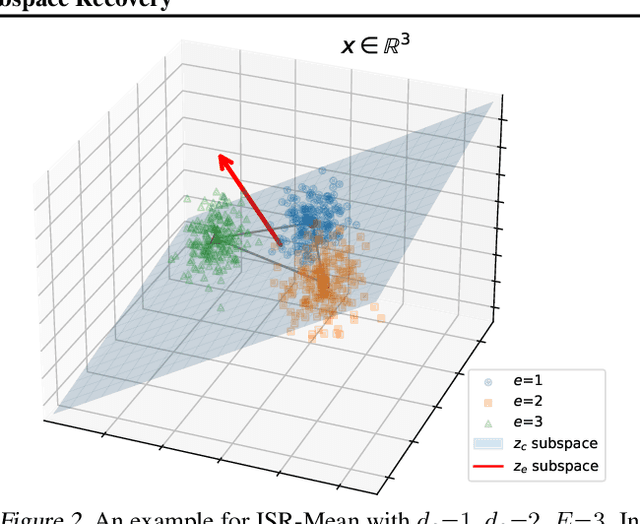
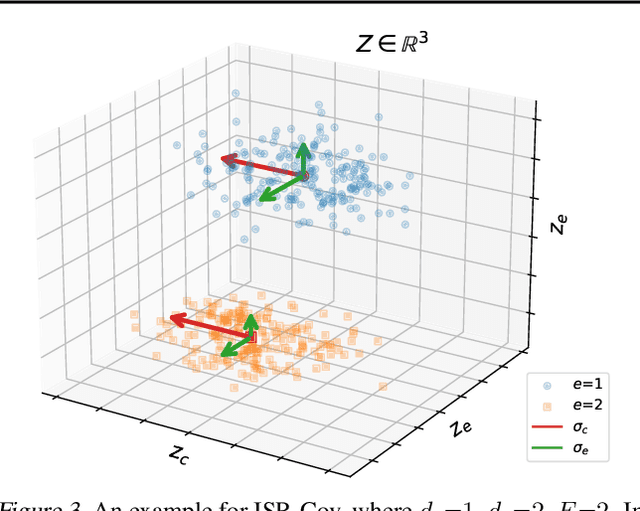
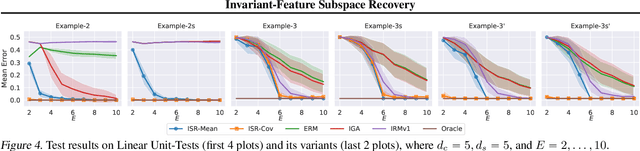
Domain generalization asks for models trained on a set of training environments to perform well on unseen test environments. Recently, a series of algorithms such as Invariant Risk Minimization (IRM) has been proposed for domain generalization. However, Rosenfeld et al. (2021) shows that in a simple linear data model, even if non-convexity issues are ignored, IRM and its extensions cannot generalize to unseen environments with less than $d_s+1$ training environments, where $d_s$ is the dimension of the spurious-feature subspace. In this paper, we propose to achieve domain generalization with Invariant-feature Subspace Recovery (ISR). Our first algorithm, ISR-Mean, can identify the subspace spanned by invariant features from the first-order moments of the class-conditional distributions, and achieve provable domain generalization with $d_s+1$ training environments under the data model of Rosenfeld et al. (2021). Our second algorithm, ISR-Cov, further reduces the required number of training environments to $O(1)$ using the information of second-order moments. Notably, unlike IRM, our algorithms bypass non-convexity issues and enjoy global convergence guarantees. Empirically, our ISRs can obtain superior performance compared with IRM on synthetic benchmarks. In addition, on three real-world image and text datasets, we show that ISR-Mean can be used as a simple yet effective post-processing method to increase the worst-case accuracy of trained models against spurious correlations and group shifts.