From Synthetic to Native: Benchmarking Multilingual Intent Classification in Logistics Customer Service

Multilingual intent classification is central to customer-service systems on global logistics platforms, where models must process noisy user queries across languages and hierarchical label spaces. Yet most existing multilingual benchmarks rely on machine-translated text, which is typically cleaner and more standardized than native customer requests and can therefore overestimate real-world robustness. We present a public benchmark for hierarchical multilingual intent classification constructed from real logistics customer-service logs. The dataset contains approximately 30K de-identified, stand-alone user queries curated from 600K historical records through filtering, LLM-assisted quality control, and human verification, and is organized into a two-level taxonomy with 13 parent and 17 leaf intents. English, Spanish, and Arabic are included as seen languages, while Indonesian, Chinese, and additional test-only languages support zero-shot evaluation. To directly measure the gap between synthetic and real evaluation, we provide paired native and machine-translated test sets and benchmark multilingual encoders, embedding models, and small language models under flat and hierarchical protocols. Results show that translated test sets substantially overestimate performance on noisy native queries, especially for long-tail intents and cross-lingual transfer, underscoring the need for more realistic multilingual intent benchmarks.

An Empirical Study of Qwen3 Quantization

The Qwen series has emerged as a leading family of open-source Large Language Models (LLMs), demonstrating remarkable capabilities in natural language understanding tasks. With the recent release of Qwen3, which exhibits superior performance across diverse benchmarks, there is growing interest in deploying these models efficiently in resource-constrained environments. Low-bit quantization presents a promising solution, yet its impact on Qwen3's performance remains underexplored. This study conducts a systematic evaluation of Qwen3's robustness under various quantization settings, aiming to uncover both opportunities and challenges in compressing this state-of-the-art model. We rigorously assess 5 existing classic post-training quantization techniques applied to Qwen3, spanning bit-widths from 1 to 8 bits, and evaluate their effectiveness across multiple datasets. Our findings reveal that while Qwen3 maintains competitive performance at moderate bit-widths, it experiences notable degradation in linguistic tasks under ultra-low precision, underscoring the persistent hurdles in LLM compression. These results emphasize the need for further research to mitigate performance loss in extreme quantization scenarios. We anticipate that this empirical analysis will provide actionable insights for advancing quantization methods tailored to Qwen3 and future LLMs, ultimately enhancing their practicality without compromising accuracy. Our project is released on https://github.com/Efficient-ML/Qwen3-Quantization and https://huggingface.co/collections/Efficient-ML/qwen3-quantization-68164450decb1c868788cb2b.

Nationality, Race, and Ethnicity Biases in and Consequences of Detecting AI-Generated Self-Presentations

This study builds on person perception and human AI interaction (HAII) theories to investigate how content and source cues, specifically race, ethnicity, and nationality, affect judgments of AI-generated content in a high-stakes self-presentation context: college applications. Results of a pre-registered experiment with a nationally representative U.S. sample (N = 644) show that content heuristics, such as linguistic style, played a dominant role in AI detection. Source heuristics, such as nationality, also emerged as a significant factor, with international students more likely to be perceived as using AI, especially when their statements included AI-sounding features. Interestingly, Asian and Hispanic applicants were more likely to be judged as AI users when labeled as domestic students, suggesting interactions between racial stereotypes and AI detection. AI attribution led to lower perceptions of personal statement quality and authenticity, as well as negative evaluations of the applicant's competence, sociability, morality, and future success.

Towards Convexity in Anomaly Detection: A New Formulation of SSLM with Unique Optimal Solutions

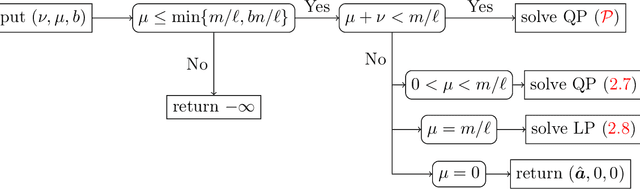
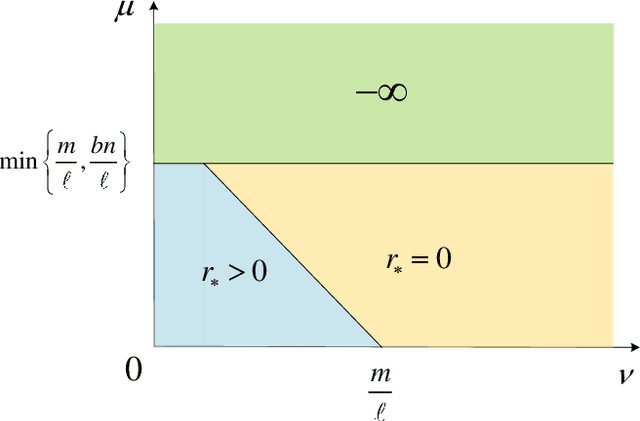
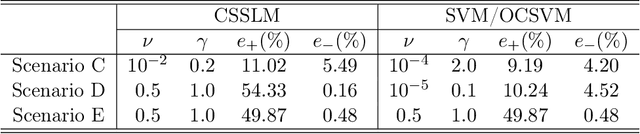
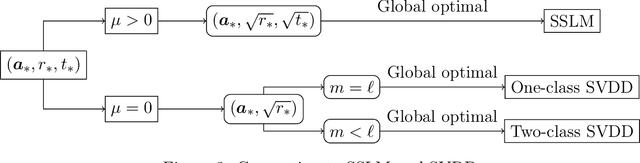
An unsolved issue in widely used methods such as Support Vector Data Description (SVDD) and Small Sphere and Large Margin SVM (SSLM) for anomaly detection is their nonconvexity, which hampers the analysis of optimal solutions in a manner similar to SVMs and limits their applicability in large-scale scenarios. In this paper, we introduce a novel convex SSLM formulation which has been demonstrated to revert to a convex quadratic programming problem for hyperparameter values of interest. Leveraging the convexity of our method, we derive numerous results that are unattainable with traditional nonconvex approaches. We conduct a thorough analysis of how hyperparameters influence the optimal solution, pointing out scenarios where optimal solutions can be trivially found and identifying instances of ill-posedness. Most notably, we establish connections between our method and traditional approaches, providing a clear determination of when the optimal solution is unique -- a task unachievable with traditional nonconvex methods. We also derive the {\nu}-property to elucidate the interactions between hyperparameters and the fractions of support vectors and margin errors in both positive and negative classes.