REAL-Prover: Retrieval Augmented Lean Prover for Mathematical Reasoning

Nowadays, formal theorem provers have made monumental progress on high-school and competition-level mathematics, but few of them generalize to more advanced mathematics. In this paper, we present REAL-Prover, a new open-source stepwise theorem prover for Lean 4 to push this boundary. This prover, based on our fine-tuned large language model (REAL-Prover-v1) and integrated with a retrieval system (Leansearch-PS), notably boosts performance on solving college-level mathematics problems. To train REAL-Prover-v1, we developed HERALD-AF, a data extraction pipeline that converts natural language math problems into formal statements, and a new open-source Lean 4 interactive environment (Jixia-interactive) to facilitate synthesis data collection. In our experiments, our prover using only supervised fine-tune achieves competitive results with a 23.7% success rate (Pass@64) on the ProofNet dataset-comparable to state-of-the-art (SOTA) models. To further evaluate our approach, we introduce FATE-M, a new benchmark focused on algebraic problems, where our prover achieves a SOTA success rate of 56.7% (Pass@64).

MIRB: Mathematical Information Retrieval Benchmark

Mathematical Information Retrieval (MIR) is the task of retrieving information from mathematical documents and plays a key role in various applications, including theorem search in mathematical libraries, answer retrieval on math forums, and premise selection in automated theorem proving. However, a unified benchmark for evaluating these diverse retrieval tasks has been lacking. In this paper, we introduce MIRB (Mathematical Information Retrieval Benchmark) to assess the MIR capabilities of retrieval models. MIRB includes four tasks: semantic statement retrieval, question-answer retrieval, premise retrieval, and formula retrieval, spanning a total of 12 datasets. We evaluate 13 retrieval models on this benchmark and analyze the challenges inherent to MIR. We hope that MIRB provides a comprehensive framework for evaluating MIR systems and helps advance the development of more effective retrieval models tailored to the mathematical domain.

A Semantic Search Engine for Mathlib4

The interactive theorem prover, Lean, enables the verification of formal mathematical proofs and is backed by an expanding community. Central to this ecosystem is its mathematical library, mathlib4, which lays the groundwork for the formalization of an expanding range of mathematical theories. However, searching for theorems in mathlib4 can be challenging. To successfully search in mathlib4, users often need to be familiar with its naming conventions or documentation strings. Therefore, creating a semantic search engine that can be used easily by individuals with varying familiarity with mathlib4 is very important. In this paper, we present a semantic search engine for mathlib4 that accepts informal queries and finds the relevant theorems. We also establish a benchmark for assessing the performance of various search engines for mathlib4.

A Comparative Study of Deep Learning and Iterative Algorithms for Joint Channel Estimation and Signal Detection

Joint channel estimation and signal detection (JCESD) is crucial in wireless communication systems, but traditional algorithms perform poorly in low signal-to-noise ratio (SNR) scenarios. Deep learning (DL) methods have been investigated, but concerns regarding computational expense and lack of validation in low-SNR settings remain. Hence, the development of a robust and low-complexity model that can deliver excellent performance across a wide range of SNRs is highly desirable. In this paper, we aim to establish a benchmark where traditional algorithms and DL methods are validated on different channel models, Doppler, and SNR settings. In particular, we propose a new DL model where the backbone network is formed by unrolling the iterative algorithm, and the hyperparameters are estimated by hypernetworks. Additionally, we adapt a lightweight DenseNet to the task of JCESD for comparison. We evaluate different methods in three aspects: generalization in terms of bit error rate (BER), robustness, and complexity. Our results indicate that DL approaches outperform traditional algorithms in the challenging low-SNR setting, while the iterative algorithm performs better in highSNR settings. Furthermore, the iterative algorithm is more robust in the presence of carrier frequency offset, whereas DL methods excel when signals are corrupted by asymmetric Gaussian noise.

CURE: Curvature Regularization For Missing Data Recovery

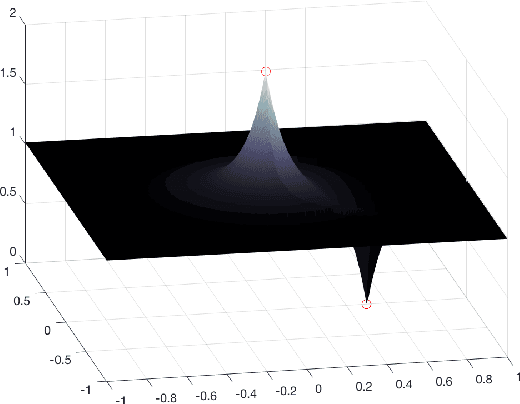
Missing data recovery is an important and yet challenging problem in imaging and data science. Successful models often adopt certain carefully chosen regularization. Recently, the low dimension manifold model (LDMM) was introduced by S.Osher et al. and shown effective in image inpainting. They observed that enforcing low dimensionality on image patch manifold serves as a good image regularizer. In this paper, we observe that having only the low dimension manifold regularization is not enough sometimes, and we need smoothness as well. For that, we introduce a new regularization by combining the low dimension manifold regularization with a higher order Curvature Regularization, and we call this new regularization CURE for short. The key step of solving CURE is to solve a biharmonic equation on a manifold. We further introduce a weighted version of CURE, called WeCURE, in a similar manner as the weighted nonlocal Laplacian (WNLL) method. Numerical experiments for image inpainting and semi-supervised learning show that the proposed CURE and WeCURE significantly outperform LDMM and WNLL respectively.