Beyond Pixels: Learning Invariant Rewards for Real-World Robotics From a Few Demonstrations

Designing reward functions that generalize beyond controlled laboratory settings remains a fundamental challenge in reinforcement learning for robotics. In open-world manipulation problems, a single task can appear in numerous variants through different object instances, positions, and camera viewpoints. Recent vision-based reward models tend to memorize specific pixel distributions and fail to generalize beyond their training conditions. To address this, we propose a framework that learns invariant symbolic reward functions from as few as five demonstrations. The insight is to shift from visual feature-fitting to the discovery of behavioral invariants: task-level properties that remain constant across diverse visual instantiations. The framework has two coupled components: a structural reward formulation that encodes task-level strategies and physical constraints while preserving optimal policy invariance, and a hybrid symbolic-numerical procedure that distills these invariants from demonstrations without online interaction. Experiments on eight Meta-World tasks and three Franka manipulation tasks demonstrate that our method achieves stronger process alignment and policy rollout ranking abilities compared to baselines, accelerating downstream policy learning. Three real-world out-of-distribution experiments further show that the same learned reward generalizes zero-shot to position, viewpoint, and object variations, enabling a single reward representation to be reused across diverse task variants in practice.

REAL-Prover: Retrieval Augmented Lean Prover for Mathematical Reasoning

Nowadays, formal theorem provers have made monumental progress on high-school and competition-level mathematics, but few of them generalize to more advanced mathematics. In this paper, we present REAL-Prover, a new open-source stepwise theorem prover for Lean 4 to push this boundary. This prover, based on our fine-tuned large language model (REAL-Prover-v1) and integrated with a retrieval system (Leansearch-PS), notably boosts performance on solving college-level mathematics problems. To train REAL-Prover-v1, we developed HERALD-AF, a data extraction pipeline that converts natural language math problems into formal statements, and a new open-source Lean 4 interactive environment (Jixia-interactive) to facilitate synthesis data collection. In our experiments, our prover using only supervised fine-tune achieves competitive results with a 23.7% success rate (Pass@64) on the ProofNet dataset-comparable to state-of-the-art (SOTA) models. To further evaluate our approach, we introduce FATE-M, a new benchmark focused on algebraic problems, where our prover achieves a SOTA success rate of 56.7% (Pass@64).

Learning to Scan: A Deep Reinforcement Learning Approach for Personalized Scanning in CT Imaging

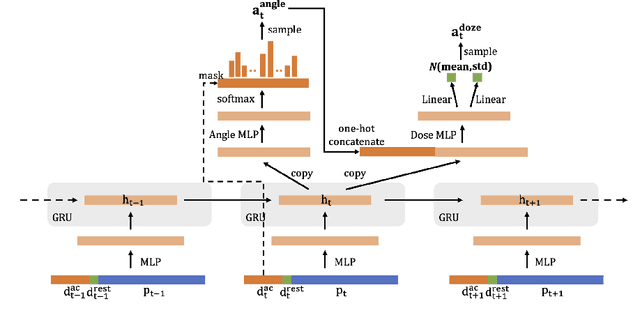
Computed Tomography (CT) takes X-ray measurements on the subjects to reconstruct tomographic images. As X-ray is radioactive, it is desirable to control the total amount of dose of X-ray for safety concerns. Therefore, we can only select a limited number of measurement angles and assign each of them limited amount of dose. Traditional methods such as compressed sensing usually randomly select the angles and equally distribute the allowed dose on them. In most CT reconstruction models, the emphasize is on designing effective image representations, while much less emphasize is on improving the scanning strategy. The simple scanning strategy of random angle selection and equal dose distribution performs well in general, but they may not be ideal for each individual subject. It is more desirable to design a personalized scanning strategy for each subject to obtain better reconstruction result. In this paper, we propose to use Reinforcement Learning (RL) to learn a personalized scanning policy to select the angles and the dose at each chosen angle for each individual subject. We first formulate the CT scanning process as an MDP, and then use modern deep RL methods to solve it. The learned personalized scanning strategy not only leads to better reconstruction results, but also shows strong generalization to be combined with different reconstruction algorithms.

Learning to Discretize: Solving 1D Scalar Conservation Laws via Deep Reinforcement Learning

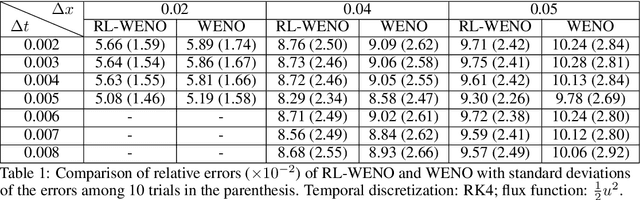
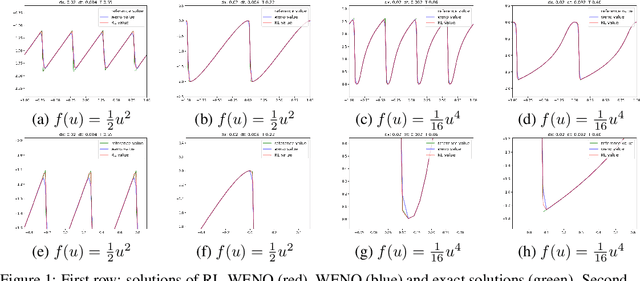
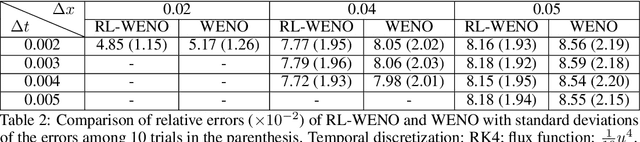
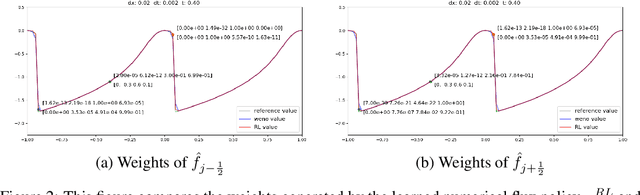
Conservation laws are considered to be fundamental laws of nature. It has broad application in many fields including physics, chemistry, biology, geology, and engineering. Solving the differential equations associated with conservation laws is a major branch in computational mathematics. Recent success of machine learning, especially deep learning, in areas such as computer vision and natural language processing, has attracted a lot of attention from the community of computational mathematics and inspired many intriguing works in combining machine learning with traditional methods. In this paper, we are the first to explore the possibility and benefit of solving nonlinear conservation laws using deep reinforcement learning. As a proof of concept, we focus on 1-dimensional scalar conservation laws. We deploy the machinery of deep reinforcement learning to train a policy network that can decide on how the numerical solutions should be approximated in a sequential and spatial-temporal adaptive manner. We will show that the problem of solving conservation laws can be naturally viewed as a sequential decision making process and the numerical schemes learned in such a way can easily enforce long-term accuracy. Furthermore, the learned policy network can determine a good local discrete approximation based on the current state of the solution, which essentially makes the proposed method a meta-learning approach. In other words, the proposed method is capable of learning how to discretize for a given situation mimicking human experts. Finally, we will provide details on how the policy network is trained, how well it performs compared with some state-of-the-art numerical solvers such as WENO schemes, and how well it generalizes.