Zichao Long
RODE-Net: Learning Ordinary Differential Equations with Randomness from Data
Jun 03, 2020



Abstract:Random ordinary differential equations (RODEs), i.e. ODEs with random parameters, are often used to model complex dynamics. Most existing methods to identify unknown governing RODEs from observed data often rely on strong prior knowledge. Extracting the governing equations from data with less prior knowledge remains a great challenge. In this paper, we propose a deep neural network, called RODE-Net, to tackle such challenge by fitting a symbolic expression of the differential equation and the distribution of parameters simultaneously. To train the RODE-Net, we first estimate the parameters of the unknown RODE using the symbolic networks \cite{long2019pde} by solving a set of deterministic inverse problems based on the measured data, and use a generative adversarial network (GAN) to estimate the true distribution of the RODE's parameters. Then, we use the trained GAN as a regularization to further improve the estimation of the ODE's parameters. The two steps are operated alternatively. Numerical results show that the proposed RODE-Net can well estimate the distribution of model parameters using simulated data and can make reliable predictions. It is worth noting that, GAN serves as a data driven regularization in RODE-Net and is more effective than the $\ell_1$ based regularization that is often used in system identifications.
Learning to Discretize: Solving 1D Scalar Conservation Laws via Deep Reinforcement Learning
Jun 11, 2019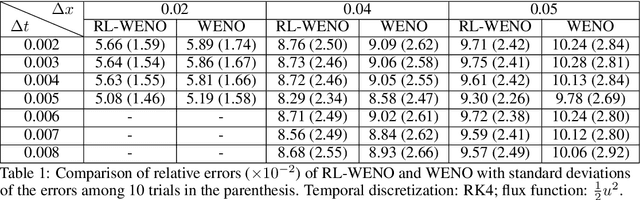
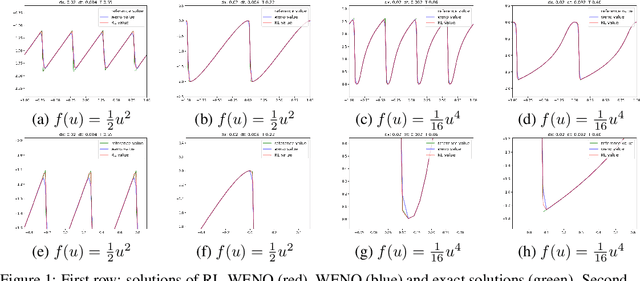
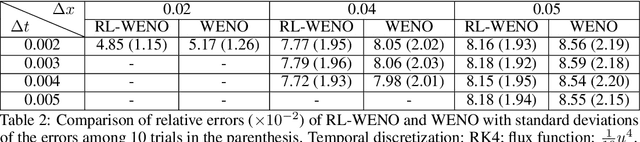
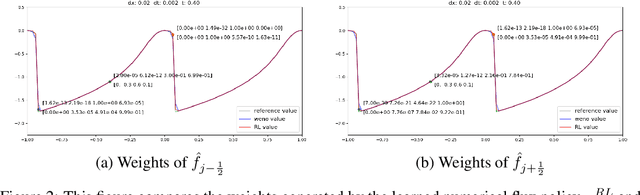
Abstract:Conservation laws are considered to be fundamental laws of nature. It has broad application in many fields including physics, chemistry, biology, geology, and engineering. Solving the differential equations associated with conservation laws is a major branch in computational mathematics. Recent success of machine learning, especially deep learning, in areas such as computer vision and natural language processing, has attracted a lot of attention from the community of computational mathematics and inspired many intriguing works in combining machine learning with traditional methods. In this paper, we are the first to explore the possibility and benefit of solving nonlinear conservation laws using deep reinforcement learning. As a proof of concept, we focus on 1-dimensional scalar conservation laws. We deploy the machinery of deep reinforcement learning to train a policy network that can decide on how the numerical solutions should be approximated in a sequential and spatial-temporal adaptive manner. We will show that the problem of solving conservation laws can be naturally viewed as a sequential decision making process and the numerical schemes learned in such a way can easily enforce long-term accuracy. Furthermore, the learned policy network can determine a good local discrete approximation based on the current state of the solution, which essentially makes the proposed method a meta-learning approach. In other words, the proposed method is capable of learning how to discretize for a given situation mimicking human experts. Finally, we will provide details on how the policy network is trained, how well it performs compared with some state-of-the-art numerical solvers such as WENO schemes, and how well it generalizes.
PDE-Net 2.0: Learning PDEs from Data with A Numeric-Symbolic Hybrid Deep Network
Nov 30, 2018



Abstract:Partial differential equations (PDEs) are commonly derived based on empirical observations. However, recent advances of technology enable us to collect and store massive amount of data, which offers new opportunities for data-driven discovery of PDEs. In this paper, we propose a new deep neural network, called PDE-Net 2.0, to discover (time-dependent) PDEs from observed dynamic data with minor prior knowledge on the underlying mechanism that drives the dynamics. The design of PDE-Net 2.0 is based on our earlier work \cite{Long2018PDE} where the original version of PDE-Net was proposed. PDE-Net 2.0 is a combination of numerical approximation of differential operators by convolutions and a symbolic multi-layer neural network for model recovery. Comparing with existing approaches, PDE-Net 2.0 has the most flexibility and expressive power by learning both differential operators and the nonlinear response function of the underlying PDE model. Numerical experiments show that the PDE-Net 2.0 has the potential to uncover the hidden PDE of the observed dynamics, and predict the dynamical behavior for a relatively long time, even in a noisy environment.
PDE-Net: Learning PDEs from Data
Jan 01, 2018



Abstract:In this paper, we present an initial attempt to learn evolution PDEs from data. Inspired by the latest development of neural network designs in deep learning, we propose a new feed-forward deep network, called PDE-Net, to fulfill two objectives at the same time: to accurately predict dynamics of complex systems and to uncover the underlying hidden PDE models. The basic idea of the proposed PDE-Net is to learn differential operators by learning convolution kernels (filters), and apply neural networks or other machine learning methods to approximate the unknown nonlinear responses. Comparing with existing approaches, which either assume the form of the nonlinear response is known or fix certain finite difference approximations of differential operators, our approach has the most flexibility by learning both differential operators and the nonlinear responses. A special feature of the proposed PDE-Net is that all filters are properly constrained, which enables us to easily identify the governing PDE models while still maintaining the expressive and predictive power of the network. These constrains are carefully designed by fully exploiting the relation between the orders of differential operators and the orders of sum rules of filters (an important concept originated from wavelet theory). We also discuss relations of the PDE-Net with some existing networks in computer vision such as Network-In-Network (NIN) and Residual Neural Network (ResNet). Numerical experiments show that the PDE-Net has the potential to uncover the hidden PDE of the observed dynamics, and predict the dynamical behavior for a relatively long time, even in a noisy environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge