Privatar: Scalable Privacy-preserving Multi-user VR via Secure Offloading

Multi-user virtual reality enables immersive interaction. However, rendering avatars for numerous participants on each headset incurs prohibitive computational overhead, limiting scalability. We introduce a framework, Privatar, to offload avatar reconstruction from headset to untrusted devices within the same local network while safeguarding attacks against adversaries capable of intercepting offloaded data. Privatar's key insight is that domain-specific knowledge of avatar reconstruction enables provably private offloading at minimal cost. (1) System level. We observe avatar reconstruction is frequency-domain decomposable via BDCT with negligible quality drop, and propose Horizontal Partitioning (HP) to keep high-energy frequency components on-device and offloads only low-energy components. HP offloads local computation while reducing information leakage to low-energy subsets only. (2) Privacy level. For individually offloaded, multi-dimensional signals without aggregation, worst-case local Differential Privacy requires prohibitive noise, ruining utility. We observe users' expression statistical distribution are slowly changing over time and trackable online, and hence propose Distribution-Aware Minimal Perturbation. DAMP minimizes noise based on each user's expression distribution to significantly reduce its effects on utility, retaining formal privacy guarantee. Combined, HP provides empirical privacy against expression identification attacks. DAMP further augments it to offer a formal guarantee against arbitrary adversaries. On a Meta Quest Pro, Privatar supports 2.37x more concurrent users at 6.5% higher reconstruction loss and 9% energy overhead, providing a better throughout-loss Pareto frontier over quantization, sparsity and local construction baselines. Privatar provides both provable privacy guarantee and stays robust against both empirical and NN-based attacks.

Architecting Secure AI Agents: Perspectives on System-Level Defenses Against Indirect Prompt Injection Attacks

AI agents, predominantly powered by large language models (LLMs), are vulnerable to indirect prompt injection, in which malicious instructions embedded in untrusted data can trigger dangerous agent actions. This position paper discusses our vision for system-level defenses against indirect prompt injection attacks. We articulate three positions: (1) dynamic replanning and security policy updates are often necessary for dynamic tasks and realistic environments; (2) certain context-dependent security decisions would still require LLMs (or other learned models), but should only be made within system designs that strictly constrain what the model can observe and decide; (3) in inherently ambiguous cases, personalization and human interaction should be treated as core design considerations. In addition to our main positions, we discuss limitations of existing benchmarks that can create a false sense of utility and security. We also highlight the value of system-level defenses, which serve as the skeleton of agentic systems by structuring and controlling agent behaviors, integrating rule-based and model-based security checks, and enabling more targeted research on model robustness and human interaction.

Privasis: Synthesizing the Largest "Public" Private Dataset from Scratch

Research involving privacy-sensitive data has always been constrained by data scarcity, standing in sharp contrast to other areas that have benefited from data scaling. This challenge is becoming increasingly urgent as modern AI agents--such as OpenClaw and Gemini Agent--are granted persistent access to highly sensitive personal information. To tackle this longstanding bottleneck and the rising risks, we present Privasis (i.e., privacy oasis), the first million-scale fully synthetic dataset entirely built from scratch--an expansive reservoir of texts with rich and diverse private information--designed to broaden and accelerate research in areas where processing sensitive social data is inevitable. Compared to existing datasets, Privasis, comprising 1.4 million records, offers orders-of-magnitude larger scale with quality, and far greater diversity across various document types, including medical history, legal documents, financial records, calendars, and text messages with a total of 55.1 million annotated attributes such as ethnicity, date of birth, workplace, etc. We leverage Privasis to construct a parallel corpus for text sanitization with our pipeline that decomposes texts and applies targeted sanitization. Our compact sanitization models (<=4B) trained on this dataset outperform state-of-the-art large language models, such as GPT-5 and Qwen-3 235B. We plan to release data, models, and code to accelerate future research on privacy-sensitive domains and agents.

Online Robust Mean Estimation

We study the problem of high-dimensional robust mean estimation in an online setting. Specifically, we consider a scenario where $n$ sensors are measuring some common, ongoing phenomenon. At each time step $t=1,2,\ldots,T$, the $i^{th}$ sensor reports its readings $x^{(i)}_t$ for that time step. The algorithm must then commit to its estimate $\mu_t$ for the true mean value of the process at time $t$. We assume that most of the sensors observe independent samples from some common distribution $X$, but an $\epsilon$-fraction of them may instead behave maliciously. The algorithm wishes to compute a good approximation $\mu$ to the true mean $\mu^\ast := \mathbf{E}[X]$. We note that if the algorithm is allowed to wait until time $T$ to report its estimate, this reduces to the well-studied problem of robust mean estimation. However, the requirement that our algorithm produces partial estimates as the data is coming in substantially complicates the situation. We prove two main results about online robust mean estimation in this model. First, if the uncorrupted samples satisfy the standard condition of $(\epsilon,\delta)$-stability, we give an efficient online algorithm that outputs estimates $\mu_t$, $t \in [T],$ such that with high probability it holds that $\|\mu-\mu^\ast\|_2 = O(\delta \log(T))$, where $\mu = (\mu_t)_{t \in [T]}$. We note that this error bound is nearly competitive with the best offline algorithms, which would achieve $\ell_2$-error of $O(\delta)$. Our second main result shows that with additional assumptions on the input (most notably that $X$ is a product distribution) there are inefficient algorithms whose error does not depend on $T$ at all.

Differentially Private Deep Learning with ModelMix

Training large neural networks with meaningful/usable differential privacy security guarantees is a demanding challenge. In this paper, we tackle this problem by revisiting the two key operations in Differentially Private Stochastic Gradient Descent (DP-SGD): 1) iterative perturbation and 2) gradient clipping. We propose a generic optimization framework, called {\em ModelMix}, which performs random aggregation of intermediate model states. It strengthens the composite privacy analysis utilizing the entropy of the training trajectory and improves the $(\epsilon, \delta)$ DP security parameters by an order of magnitude. We provide rigorous analyses for both the utility guarantees and privacy amplification of ModelMix. In particular, we present a formal study on the effect of gradient clipping in DP-SGD, which provides theoretical instruction on how hyper-parameters should be selected. We also introduce a refined gradient clipping method, which can further sharpen the privacy loss in private learning when combined with ModelMix. Thorough experiments with significant privacy/utility improvement are presented to support our theory. We train a Resnet-20 network on CIFAR10 with $70.4\%$ accuracy via ModelMix given $(\epsilon=8, \delta=10^{-5})$ DP-budget, compared to the same performance but with $(\epsilon=145.8,\delta=10^{-5})$ using regular DP-SGD; assisted with additional public low-dimensional gradient embedding, one can further improve the accuracy to $79.1\%$ with $(\epsilon=6.1, \delta=10^{-5})$ DP-budget, compared to the same performance but with $(\epsilon=111.2, \delta=10^{-5})$ without ModelMix.

High Dimensional Differentially Private Stochastic Optimization with Heavy-tailed Data

As one of the most fundamental problems in machine learning, statistics and differential privacy, Differentially Private Stochastic Convex Optimization (DP-SCO) has been extensively studied in recent years. However, most of the previous work can only handle either regular data distribution or irregular data in the low dimensional space case. To better understand the challenges arising from irregular data distribution, in this paper we provide the first study on the problem of DP-SCO with heavy-tailed data in the high dimensional space. In the first part we focus on the problem over some polytope constraint (such as the $\ell_1$-norm ball). We show that if the loss function is smooth and its gradient has bounded second order moment, it is possible to get a (high probability) error bound (excess population risk) of $\tilde{O}(\frac{\log d}{(n\epsilon)^\frac{1}{3}})$ in the $\epsilon$-DP model, where $n$ is the sample size and $d$ is the dimensionality of the underlying space. Next, for LASSO, if the data distribution that has bounded fourth-order moments, we improve the bound to $\tilde{O}(\frac{\log d}{(n\epsilon)^\frac{2}{5}})$ in the $(\epsilon, \delta)$-DP model. In the second part of the paper, we study sparse learning with heavy-tailed data. We first revisit the sparse linear model and propose a truncated DP-IHT method whose output could achieve an error of $\tilde{O}(\frac{s^{*2}\log d}{n\epsilon})$, where $s^*$ is the sparsity of the underlying parameter. Then we study a more general problem over the sparsity ({\em i.e.,} $\ell_0$-norm) constraint, and show that it is possible to achieve an error of $\tilde{O}(\frac{s^{*\frac{3}{2}}\log d}{n\epsilon})$, which is also near optimal up to a factor of $\tilde{O}{(\sqrt{s^*})}$, if the loss function is smooth and strongly convex.

On Differentially Private Stochastic Convex Optimization with Heavy-tailed Data

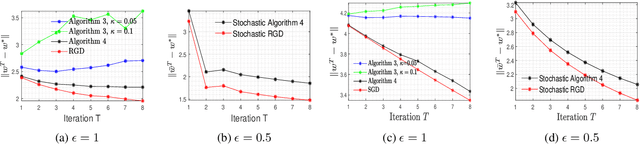
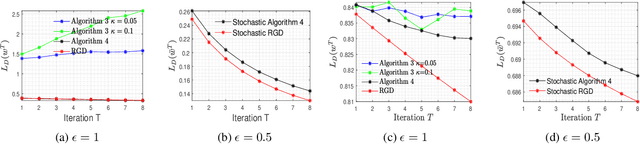
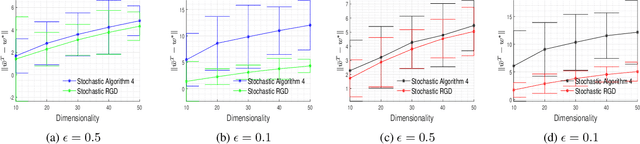
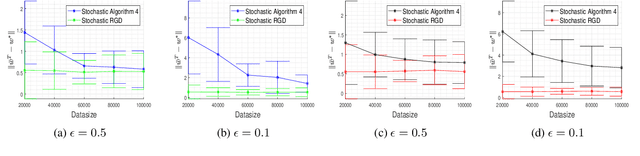
In this paper, we consider the problem of designing Differentially Private (DP) algorithms for Stochastic Convex Optimization (SCO) on heavy-tailed data. The irregularity of such data violates some key assumptions used in almost all existing DP-SCO and DP-ERM methods, resulting in failure to provide the DP guarantees. To better understand this type of challenges, we provide in this paper a comprehensive study of DP-SCO under various settings. First, we consider the case where the loss function is strongly convex and smooth. For this case, we propose a method based on the sample-and-aggregate framework, which has an excess population risk of $\tilde{O}(\frac{d^3}{n\epsilon^4})$ (after omitting other factors), where $n$ is the sample size and $d$ is the dimensionality of the data. Then, we show that with some additional assumptions on the loss functions, it is possible to reduce the \textit{expected} excess population risk to $\tilde{O}(\frac{ d^2}{ n\epsilon^2 })$. To lift these additional conditions, we also provide a gradient smoothing and trimming based scheme to achieve excess population risks of $\tilde{O}(\frac{ d^2}{n\epsilon^2})$ and $\tilde{O}(\frac{d^\frac{2}{3}}{(n\epsilon^2)^\frac{1}{3}})$ for strongly convex and general convex loss functions, respectively, \textit{with high probability}. Experiments suggest that our algorithms can effectively deal with the challenges caused by data irregularity.

On Privacy-preserving Decentralized Optimization through Alternating Direction Method of Multipliers

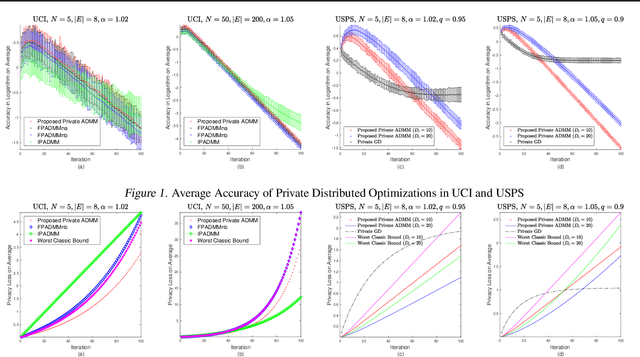
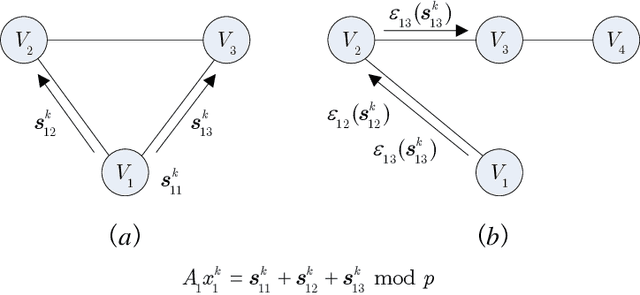
Privacy concerns with sensitive data in machine learning are receiving increasing attention. In this paper, we study privacy-preserving distributed learning under the framework of Alternating Direction Method of Multipliers (ADMM). While secure distributed learning has been previously exploited in cryptographic or non-cryptographic (noise perturbation) approaches, it comes at a cost of either prohibitive computation overhead or a heavy loss of accuracy. Moreover, convergence in noise perturbation is hardly explored in existing privacy-preserving ADMM schemes. In this work, we propose two modified private ADMM schemes in the scenario of peer-to-peer semi-honest agents: First, for bounded colluding agents, we show that with merely linear secret sharing, information-theoretically private distributed optimization can be achieved. Second, using the notion of differential privacy, we propose first-order approximation based ADMM schemes with random parameters. We prove that the proposed private ADMM schemes can be implemented with a linear convergence rate and with a sharpened privacy loss bound in relation to prior work. Finally, we provide experimental results to support the theory.

Statistical Robust Chinese Remainder Theorem for Multiple Numbers: Wrapped Gaussian Mixture Model

Generalized Chinese Remainder Theorem (CRT) has been shown to be a powerful approach to solve the ambiguity resolution problem. However, with its close relationship to number theory, study in this area is mainly from a coding theory perspective under deterministic conditions. Nevertheless, it can be proved that even with the best deterministic condition known, the probability of success in robust reconstruction degrades exponentially as the number of estimand increases. In this paper, we present the first rigorous analysis on the underlying statistical model of CRT-based multiple parameter estimation, where a generalized Gaussian mixture with background knowledge on samplings is proposed. To address the problem, two novel approaches are introduced. One is to directly calculate the conditional maximal a posteriori probability (MAP) estimation of residue clustering, and the other is to iteratively search for MAP of both common residues and clustering. Moreover, remainder error-correcting codes are introduced to improve the robustness further. It is shown that this statistically based scheme achieves much stronger robustness compared to state-of-the-art deterministic schemes, especially in low and median Signal Noise Ratio (SNR) scenarios.