On Differentially Private Stochastic Convex Optimization with Heavy-tailed Data

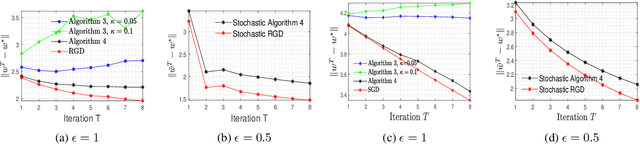
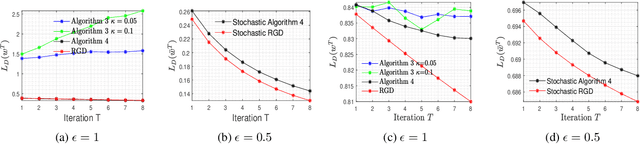
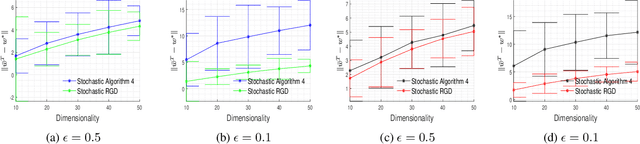
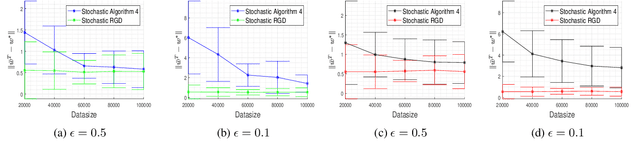
In this paper, we consider the problem of designing Differentially Private (DP) algorithms for Stochastic Convex Optimization (SCO) on heavy-tailed data. The irregularity of such data violates some key assumptions used in almost all existing DP-SCO and DP-ERM methods, resulting in failure to provide the DP guarantees. To better understand this type of challenges, we provide in this paper a comprehensive study of DP-SCO under various settings. First, we consider the case where the loss function is strongly convex and smooth. For this case, we propose a method based on the sample-and-aggregate framework, which has an excess population risk of $\tilde{O}(\frac{d^3}{n\epsilon^4})$ (after omitting other factors), where $n$ is the sample size and $d$ is the dimensionality of the data. Then, we show that with some additional assumptions on the loss functions, it is possible to reduce the \textit{expected} excess population risk to $\tilde{O}(\frac{ d^2}{ n\epsilon^2 })$. To lift these additional conditions, we also provide a gradient smoothing and trimming based scheme to achieve excess population risks of $\tilde{O}(\frac{ d^2}{n\epsilon^2})$ and $\tilde{O}(\frac{d^\frac{2}{3}}{(n\epsilon^2)^\frac{1}{3}})$ for strongly convex and general convex loss functions, respectively, \textit{with high probability}. Experiments suggest that our algorithms can effectively deal with the challenges caused by data irregularity.

On Privacy-preserving Decentralized Optimization through Alternating Direction Method of Multipliers

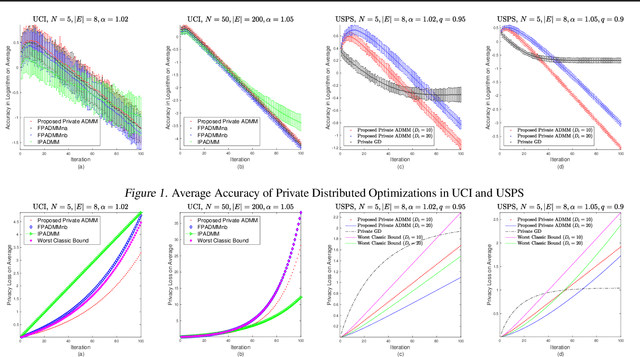
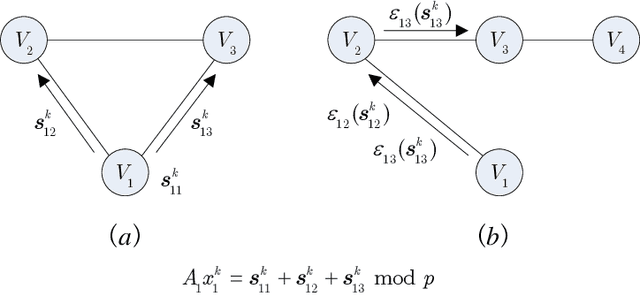
Privacy concerns with sensitive data in machine learning are receiving increasing attention. In this paper, we study privacy-preserving distributed learning under the framework of Alternating Direction Method of Multipliers (ADMM). While secure distributed learning has been previously exploited in cryptographic or non-cryptographic (noise perturbation) approaches, it comes at a cost of either prohibitive computation overhead or a heavy loss of accuracy. Moreover, convergence in noise perturbation is hardly explored in existing privacy-preserving ADMM schemes. In this work, we propose two modified private ADMM schemes in the scenario of peer-to-peer semi-honest agents: First, for bounded colluding agents, we show that with merely linear secret sharing, information-theoretically private distributed optimization can be achieved. Second, using the notion of differential privacy, we propose first-order approximation based ADMM schemes with random parameters. We prove that the proposed private ADMM schemes can be implemented with a linear convergence rate and with a sharpened privacy loss bound in relation to prior work. Finally, we provide experimental results to support the theory.