On Privacy-preserving Decentralized Optimization through Alternating Direction Method of Multipliers

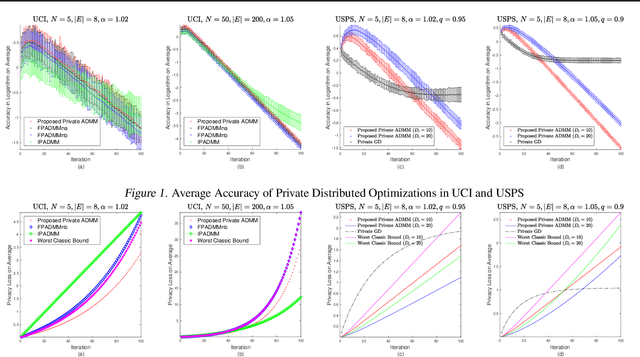
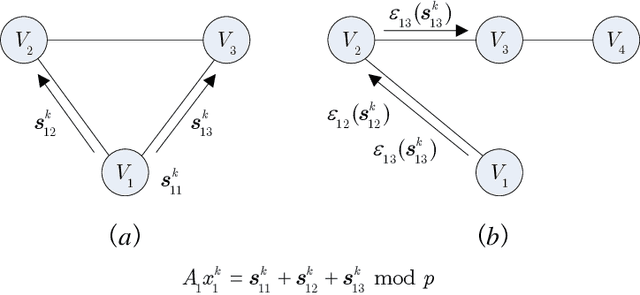
Privacy concerns with sensitive data in machine learning are receiving increasing attention. In this paper, we study privacy-preserving distributed learning under the framework of Alternating Direction Method of Multipliers (ADMM). While secure distributed learning has been previously exploited in cryptographic or non-cryptographic (noise perturbation) approaches, it comes at a cost of either prohibitive computation overhead or a heavy loss of accuracy. Moreover, convergence in noise perturbation is hardly explored in existing privacy-preserving ADMM schemes. In this work, we propose two modified private ADMM schemes in the scenario of peer-to-peer semi-honest agents: First, for bounded colluding agents, we show that with merely linear secret sharing, information-theoretically private distributed optimization can be achieved. Second, using the notion of differential privacy, we propose first-order approximation based ADMM schemes with random parameters. We prove that the proposed private ADMM schemes can be implemented with a linear convergence rate and with a sharpened privacy loss bound in relation to prior work. Finally, we provide experimental results to support the theory.