Rational Linkages: From Poses to 3D-printed Prototypes

In this paper, a set of tools is introduced that simplifies the synthesis and rapid-prototyping of single-loop rational kinematic chains. It allows the user to perform rational motion interpolation of up to four given poses and yields the design parameters of a linkage that can execute this motion. The package also provides a visualization of the output and performs a self-collision analysis with the possibility to adapt the design parameters. The results can be imported into CAD-systems for fast 3D printing.

A Complete Characterization of Bounded Motion Polynomials Admitting a Factorization with Linear Factors

Motion polynomials (polynomials over the dual quaternions with the non-zero real norm) describe rational motions. We present a necessary and sufficient condition for reduced bounded motion polynomials to admit factorizations into linear factors, and we give an algorithm to compute them. We can use those linear factors to construct mechanisms because the factorization corresponds to the decomposition of the rational motion into simple rotations or translations. Bounded motion polynomials always admit a factorization into linear factors after multiplying with a suitable real or quaternion polynomial. Our criterion for factorizability allows us to improve on earlier algorithms to compute a suitable real or quaternion polynomial co-factor.

A Multi-Bennett 8R Mechanism Obtained From Factorization of Bivariate Motion Polynomials

We present a closed-loop 8R mechanism with two degrees of freedom whose motion exhibits curious properties. In any point of a two-dimensional component of its configuration variety it is possible to fix every second joint while retaining one degree of freedom. This shows that the even and the odd axes, respectively, always form a Bennett mechanism. In this mechanism, opposite distances and angles are equal and all offsets are zero. The 8R mechanism has four "totally aligned" configurations in which the common normals of any pair of consecutive axes coincide.

Rational Motions with Generic Trajectories of Low Degree

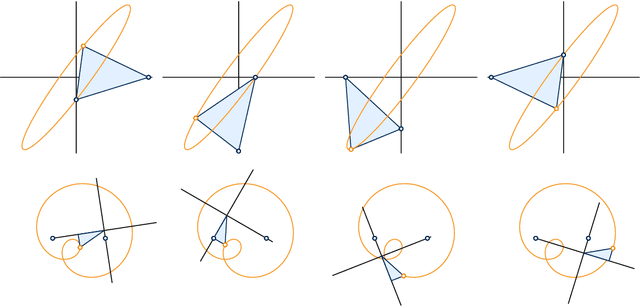
The trajectories of a rational motion given by a polynomial of degree n in the dual quaternion model of rigid body displacements are generically of degree 2n. In this article we study those exceptional motions whose trajectory degree is lower. An algebraic criterion for this drop of degree is existence of certain right factors, a geometric criterion involves one of two families of rulings on an invariant quadric. Our characterizations allow the systematic construction of rational motions with exceptional degree reduction and explain why the trajectory degrees of a rational motion and its inverse motion can be different.

Optimal Synthesis of Overconstrained 6R Linkages by Curve Evolution

The paper presents an optimal synthesis of overconstrained linkages, based on the factorization of rational curves (representing one parametric motions) contained in Study's quadric. The group of Euclidean displacements is embedded in a affine space where a metric between motions based on the homogeneous mass distribution of the end effector is used to evolve the curves such that they are fitted to a set of target poses. The metric will measure the distance (in Euclidean sense) between the two resulting vectors of the feature points displaced by the two motions. The evolution is driven by the normal velocity of the curve projected in the direction of the target points. In the end we present an example for the optimal synthesis of an overconstrained $6R$ linkage by choosing a set of target poses and explaining in steps how this approach is implemented.

Kempe's Universality Theorem for Rational Space Curves

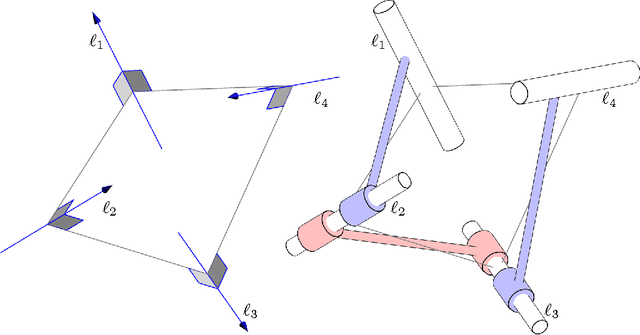
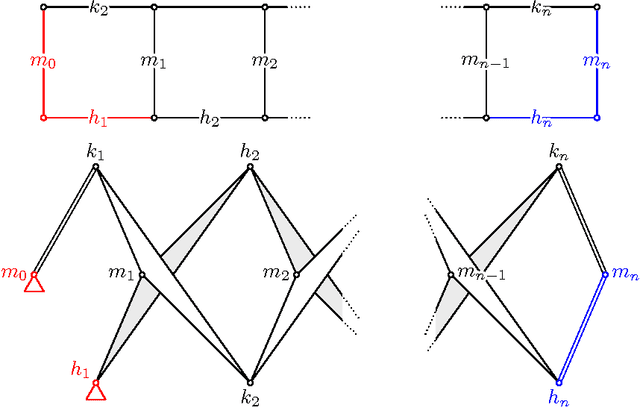
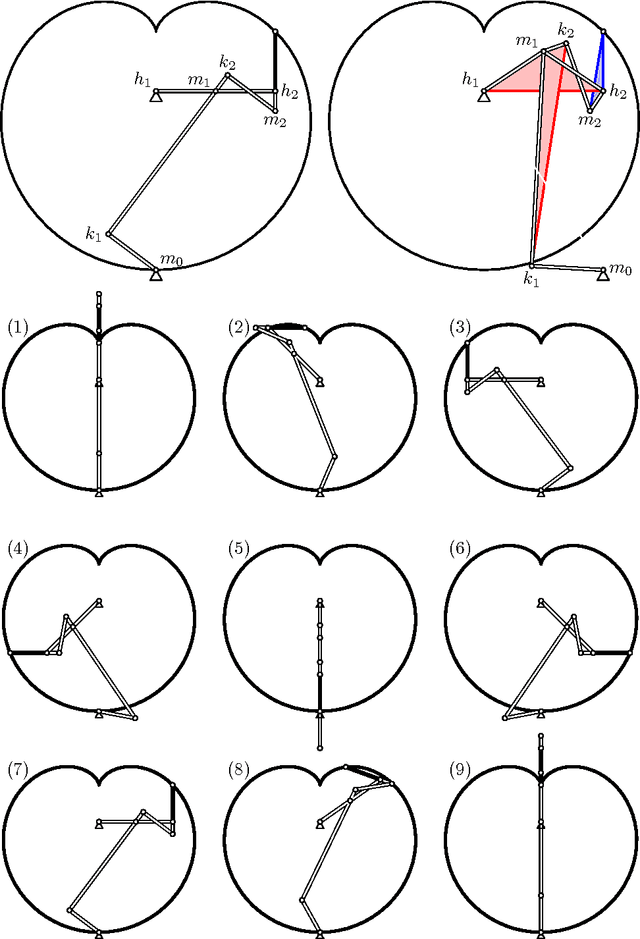
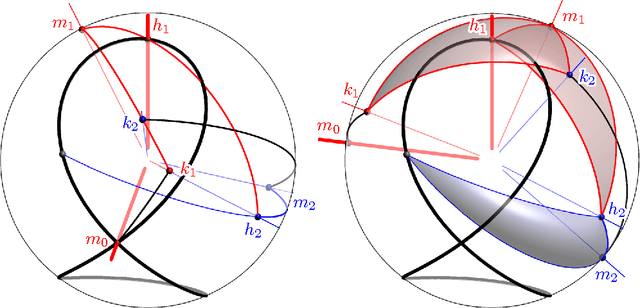
We prove that every bounded rational space curve of degree d and circularity c can be drawn by a linkage with 9/2 d - 6c + 1 revolute joints. Our proof is based on two ingredients. The first one is the factorization theory of motion polynomials. The second one is the construction of a motion polynomial of minimum degree with given orbit. Our proof also gives the explicity construction of the linkage.

The Kinematic Image of RR, PR, and RP Dyads

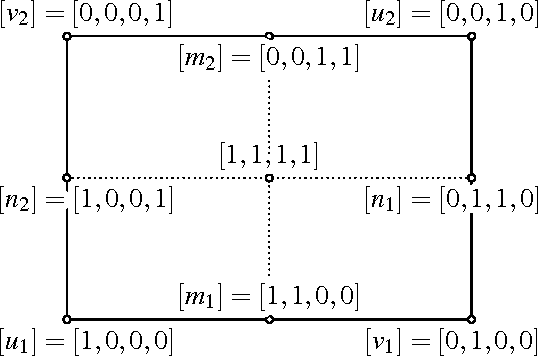
We provide necessary and sufficient conditions for admissible transformations in the projectivised dual quaternion model of rigid body displacements and we characterise constraint varieties of dyads with revolute and prismatic joints in this model. Projective transformations induced by coordinate changes in moving and/or fixed frame fix the quadrics of a pencil and preserve the two families of rulings of an exceptional three-dimensional quadric. The constraint variety of a dyad with two revolute joints is a regular ruled quadric in a three-space that contains a "null quadrilateral". If a revolute joint is replaced by a prismatic joint, this quadrilateral collapses into a pair of conjugate complex null lines and a real line but these properties are not sufficient to characterise such dyads. We provide a complete characterisation by introducing a new invariant, the "fiber projectivity", and we present examples that demonstrate its potential to explain hitherto not sufficiently well understood phenomena.

The Kinematic Image of 2R Dyads and Exact Synthesis of 5R Linkages

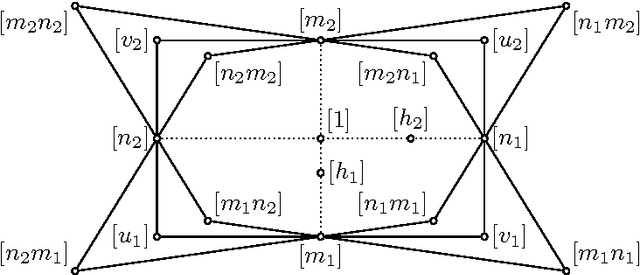
We characterise the kinematic image of the constraint variety of a 2R dyad as a regular ruled quadric in a 3-space that contains a "null quadrilateral". Three prescribed poses determine, in general, two such quadrics. This allows us to modify a recent algorithm for the synthesis of 6R linkages in such a way that two consecutive revolute axes coincide, thus producing a 5R linkage. Using the classical geometry of twisted cubics on a quadric, we explain some of the peculiar properties of the the resulting synthesis procedure for 5R linkages.

From the Fundamental Theorem of Algebra to Kempe's Universality Theorem

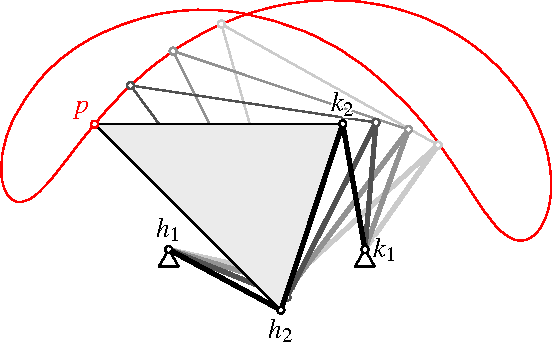
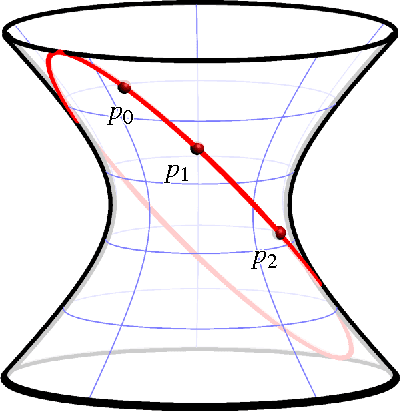
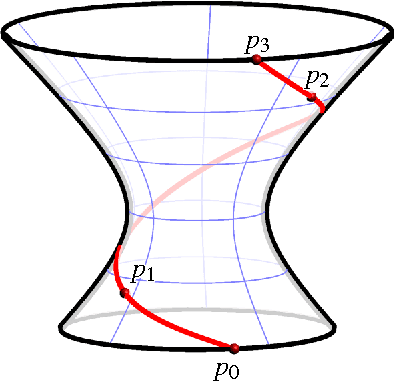
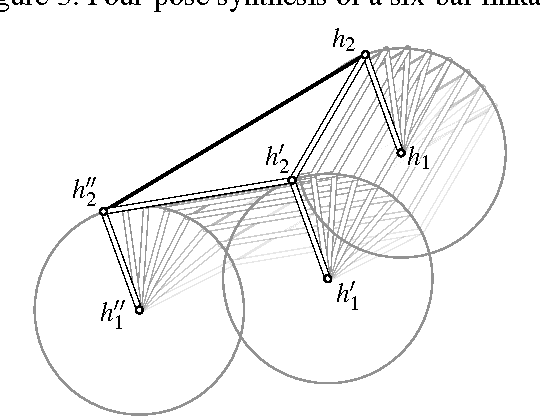
This article provides a gentle introduction for a general mathematical audience to the factorization theory of motion polynomials and its application in mechanism science. This theory connects in a rather unexpected way a seemingly abstract mathematical topic, the non-unique factorization of certain polynomials over the ring of dual quaternions, with engineering applications. Four years after its introduction, it is already clear how beneficial it has been to both fields.

7R Darboux Linkages by Factorization of Motion Polynomials

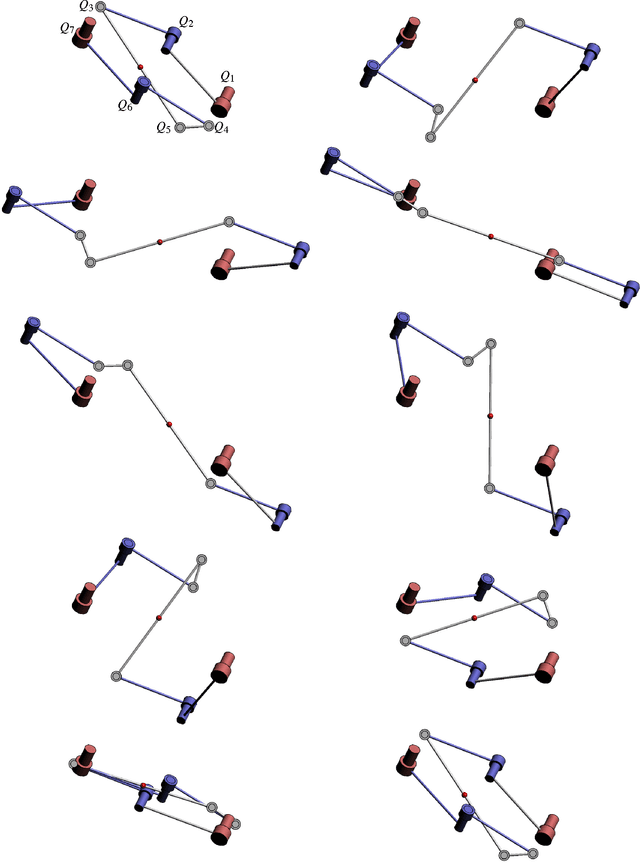
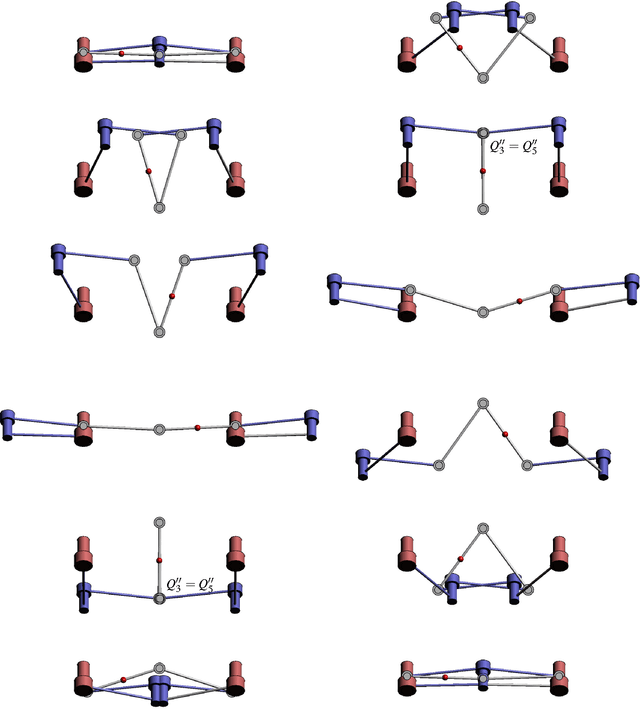
In this paper, we construct two types of 7R closed single loop linkages by combining different factorizations of a general (non-vertical) Darboux motion. These factorizations are obtained by extensions of a factorization algorithm for a generic rational motion. The first type of 7R linkages has several one-dimensional configuration components and one of them corresponds to the Darboux motion. The other type is a 7R linkage with two degrees of freedom and without one-dimensional component. The Darboux motion is a curve in an irreducible two dimensional configuration component.