The Kinematic Image of RR, PR, and RP Dyads
Paper and Code
Jul 27, 2016


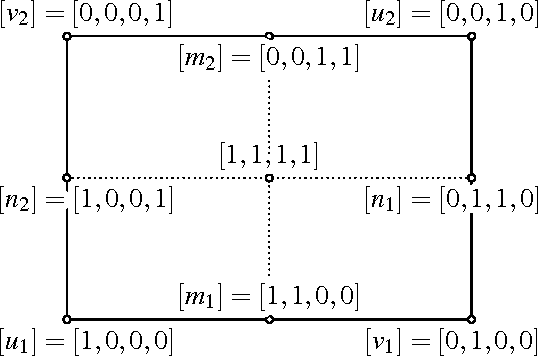
We provide necessary and sufficient conditions for admissible transformations in the projectivised dual quaternion model of rigid body displacements and we characterise constraint varieties of dyads with revolute and prismatic joints in this model. Projective transformations induced by coordinate changes in moving and/or fixed frame fix the quadrics of a pencil and preserve the two families of rulings of an exceptional three-dimensional quadric. The constraint variety of a dyad with two revolute joints is a regular ruled quadric in a three-space that contains a "null quadrilateral". If a revolute joint is replaced by a prismatic joint, this quadrilateral collapses into a pair of conjugate complex null lines and a real line but these properties are not sufficient to characterise such dyads. We provide a complete characterisation by introducing a new invariant, the "fiber projectivity", and we present examples that demonstrate its potential to explain hitherto not sufficiently well understood phenomena.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge