Optimal Synthesis of Overconstrained 6R Linkages by Curve Evolution

The paper presents an optimal synthesis of overconstrained linkages, based on the factorization of rational curves (representing one parametric motions) contained in Study's quadric. The group of Euclidean displacements is embedded in a affine space where a metric between motions based on the homogeneous mass distribution of the end effector is used to evolve the curves such that they are fitted to a set of target poses. The metric will measure the distance (in Euclidean sense) between the two resulting vectors of the feature points displaced by the two motions. The evolution is driven by the normal velocity of the curve projected in the direction of the target points. In the end we present an example for the optimal synthesis of an overconstrained $6R$ linkage by choosing a set of target poses and explaining in steps how this approach is implemented.

The Kinematic Image of RR, PR, and RP Dyads

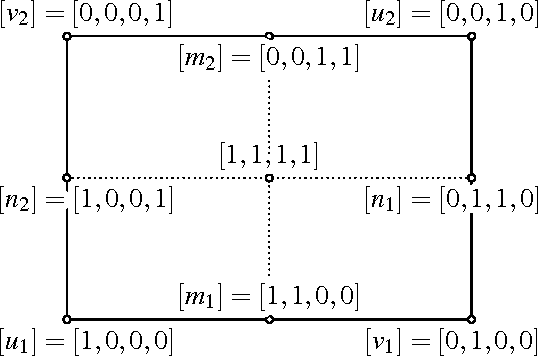
We provide necessary and sufficient conditions for admissible transformations in the projectivised dual quaternion model of rigid body displacements and we characterise constraint varieties of dyads with revolute and prismatic joints in this model. Projective transformations induced by coordinate changes in moving and/or fixed frame fix the quadrics of a pencil and preserve the two families of rulings of an exceptional three-dimensional quadric. The constraint variety of a dyad with two revolute joints is a regular ruled quadric in a three-space that contains a "null quadrilateral". If a revolute joint is replaced by a prismatic joint, this quadrilateral collapses into a pair of conjugate complex null lines and a real line but these properties are not sufficient to characterise such dyads. We provide a complete characterisation by introducing a new invariant, the "fiber projectivity", and we present examples that demonstrate its potential to explain hitherto not sufficiently well understood phenomena.

The Kinematic Image of 2R Dyads and Exact Synthesis of 5R Linkages

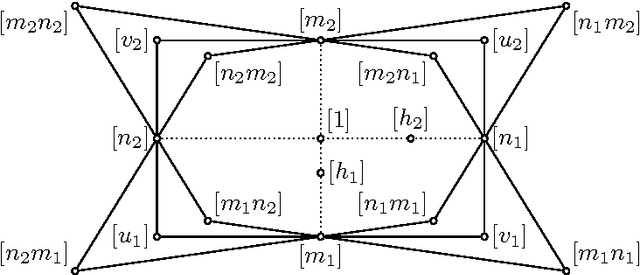
We characterise the kinematic image of the constraint variety of a 2R dyad as a regular ruled quadric in a 3-space that contains a "null quadrilateral". Three prescribed poses determine, in general, two such quadrics. This allows us to modify a recent algorithm for the synthesis of 6R linkages in such a way that two consecutive revolute axes coincide, thus producing a 5R linkage. Using the classical geometry of twisted cubics on a quadric, we explain some of the peculiar properties of the the resulting synthesis procedure for 5R linkages.

Factorization of Rational Motions: A Survey with Examples and Applications

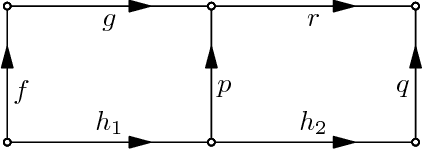
Since its introduction in 2012, the factorization theory for rational motions quickly evolved and found applications in theoretical and applied mechanism science. We provide an accessible introduction to motion factorization with many examples, summarize recent developments and hint at some new applications. In particular, we provide pseudo-code for the generic factorization algorithm, demonstrate how to find a replacement linkage for a special case in the synthesis of Bennett mechanisms and, as an example of non-generic factorization, synthesize open chains for circular and elliptic translations.