A Complete Characterization of Bounded Motion Polynomials Admitting a Factorization with Linear Factors

Motion polynomials (polynomials over the dual quaternions with the non-zero real norm) describe rational motions. We present a necessary and sufficient condition for reduced bounded motion polynomials to admit factorizations into linear factors, and we give an algorithm to compute them. We can use those linear factors to construct mechanisms because the factorization corresponds to the decomposition of the rational motion into simple rotations or translations. Bounded motion polynomials always admit a factorization into linear factors after multiplying with a suitable real or quaternion polynomial. Our criterion for factorizability allows us to improve on earlier algorithms to compute a suitable real or quaternion polynomial co-factor.

A Multi-Bennett 8R Mechanism Obtained From Factorization of Bivariate Motion Polynomials

We present a closed-loop 8R mechanism with two degrees of freedom whose motion exhibits curious properties. In any point of a two-dimensional component of its configuration variety it is possible to fix every second joint while retaining one degree of freedom. This shows that the even and the odd axes, respectively, always form a Bennett mechanism. In this mechanism, opposite distances and angles are equal and all offsets are zero. The 8R mechanism has four "totally aligned" configurations in which the common normals of any pair of consecutive axes coincide.

Analysis of a 3-RUU Parallel Manipulator

The aim of this paper is to give a detailed examination of the input and output singularities of a 3-RUU parallel manipulator in the translational operation mode. This task is achieved by using algebraic constraint equations. For this type of manipulator a complete workspace representation in Study coordinates is presented after elimination of the input parameters. Both, input and output singularities are mapped into a Study subspace as well as into the joint space. Therewith a detailed singularity investigation of the translational operation mode of a 3-RUU parallel manipulator is provided. This paper is an extended version of a previous publication. The addendum comprises the discovery of a possible transition between two operation modes as well as a self motion and an examination of another component of the output singularity surface, most of them for arbitrary design parameters.

Rational Motions with Generic Trajectories of Low Degree

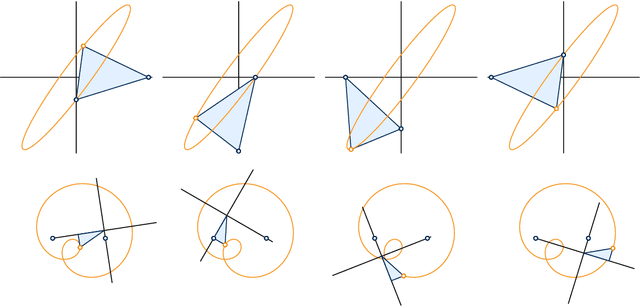
The trajectories of a rational motion given by a polynomial of degree n in the dual quaternion model of rigid body displacements are generically of degree 2n. In this article we study those exceptional motions whose trajectory degree is lower. An algebraic criterion for this drop of degree is existence of certain right factors, a geometric criterion involves one of two families of rulings on an invariant quadric. Our characterizations allow the systematic construction of rational motions with exceptional degree reduction and explain why the trajectory degrees of a rational motion and its inverse motion can be different.

The Kinematic Image of RR, PR, and RP Dyads

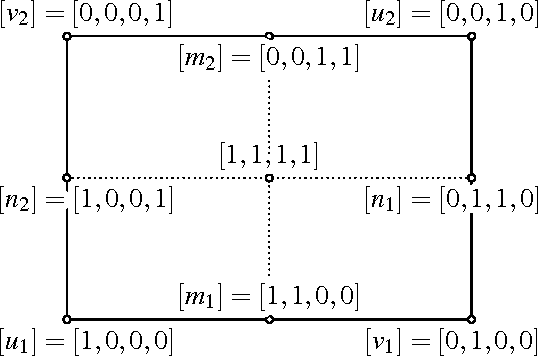
We provide necessary and sufficient conditions for admissible transformations in the projectivised dual quaternion model of rigid body displacements and we characterise constraint varieties of dyads with revolute and prismatic joints in this model. Projective transformations induced by coordinate changes in moving and/or fixed frame fix the quadrics of a pencil and preserve the two families of rulings of an exceptional three-dimensional quadric. The constraint variety of a dyad with two revolute joints is a regular ruled quadric in a three-space that contains a "null quadrilateral". If a revolute joint is replaced by a prismatic joint, this quadrilateral collapses into a pair of conjugate complex null lines and a real line but these properties are not sufficient to characterise such dyads. We provide a complete characterisation by introducing a new invariant, the "fiber projectivity", and we present examples that demonstrate its potential to explain hitherto not sufficiently well understood phenomena.