A Complete Characterization of Bounded Motion Polynomials Admitting a Factorization with Linear Factors

Motion polynomials (polynomials over the dual quaternions with the non-zero real norm) describe rational motions. We present a necessary and sufficient condition for reduced bounded motion polynomials to admit factorizations into linear factors, and we give an algorithm to compute them. We can use those linear factors to construct mechanisms because the factorization corresponds to the decomposition of the rational motion into simple rotations or translations. Bounded motion polynomials always admit a factorization into linear factors after multiplying with a suitable real or quaternion polynomial. Our criterion for factorizability allows us to improve on earlier algorithms to compute a suitable real or quaternion polynomial co-factor.

Classification of Higher Mobility Linkages

We provide a complete classification of paradoxical $n$-linkages, $n\geq6$ whose mobility is $n-4$ or higher containing $R$, $P$ or $H$ joints. We also explicitly write down strong necessary conditions for $nR$-linkages of mobility $n-5$.

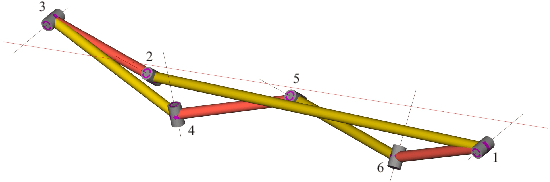
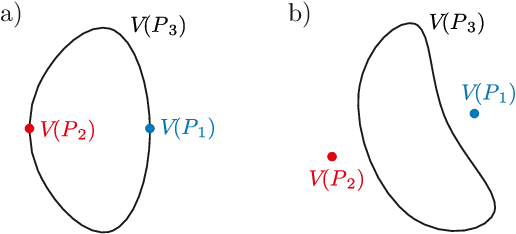
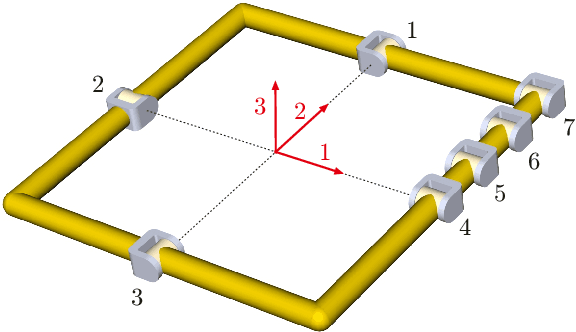
Mechanism Singularities Revisited from an Algebraic Viewpoint

It has become obvious that certain singular phenomena cannot be explained by a mere investigation of the configuration space, defined as the solution set of the loop closure equations. For example, it was observed that a particular 6R linkage, constructed by a combination of two Goldberg 5R linkages, exhibits kinematic singularities at a smooth point in its configuration space. Such problems are addressed in this paper. To this end, an algebraic framework is used in which the constraints are formulated as polynomial equations using Study parameters. The algebraic object of study is the ideal generated by the constraint equations (the constraint ideal). Using basic tools from commutative algebra and algebraic geometry (primary decomposition, Hilbert's Nullstellensatz), the special phenomenon is related to the fact that the constraint ideal is not a radical ideal. With a primary decomposition of the constraint ideal, the associated prime ideal of one primary ideal contains strictly into the associated prime ideal of another primary ideal which also gives the smooth configuration curve. This analysis is extended to shaky and kinematotropic linkages, for which examples are presented.

Kempe's Universality Theorem for Rational Space Curves

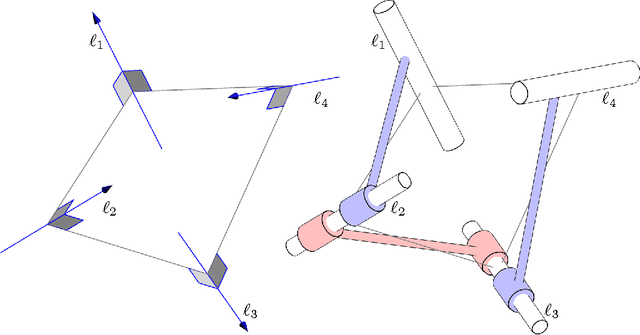
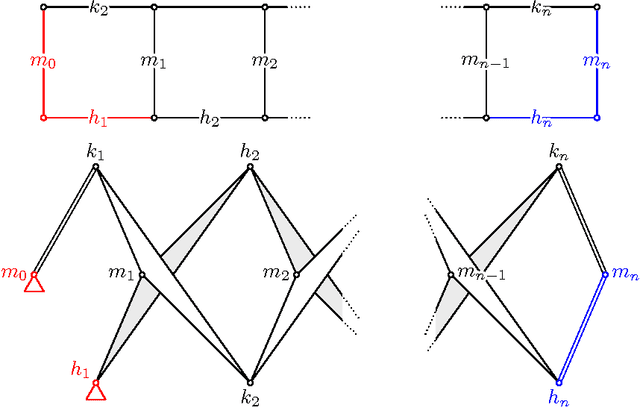
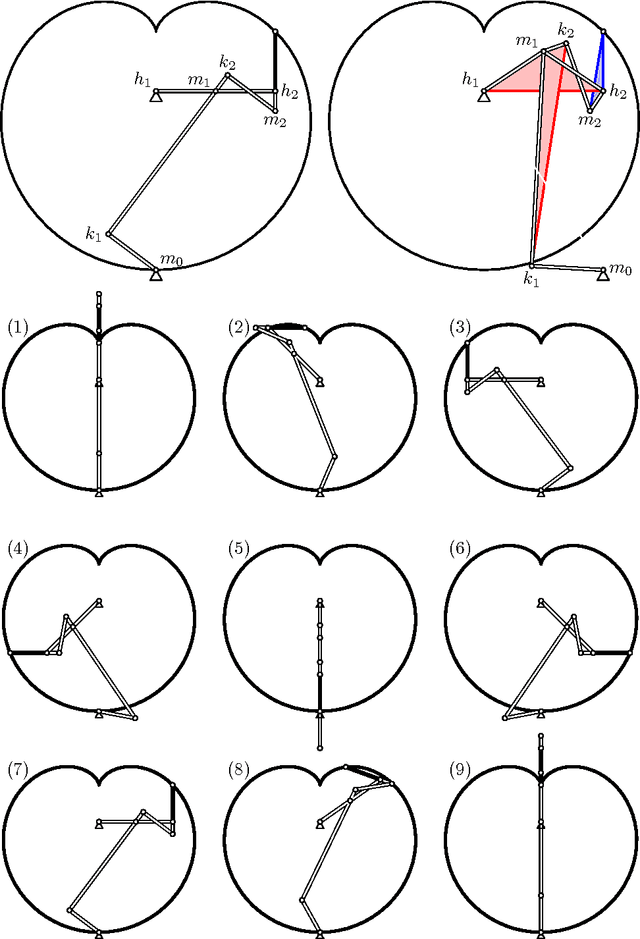
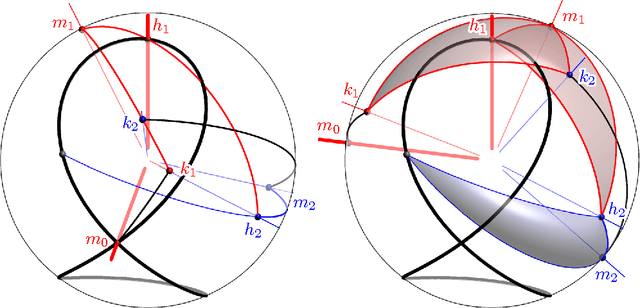
We prove that every bounded rational space curve of degree d and circularity c can be drawn by a linkage with 9/2 d - 6c + 1 revolute joints. Our proof is based on two ingredients. The first one is the factorization theory of motion polynomials. The second one is the construction of a motion polynomial of minimum degree with given orbit. Our proof also gives the explicity construction of the linkage.

Planar Linkages Following a Prescribed Motion

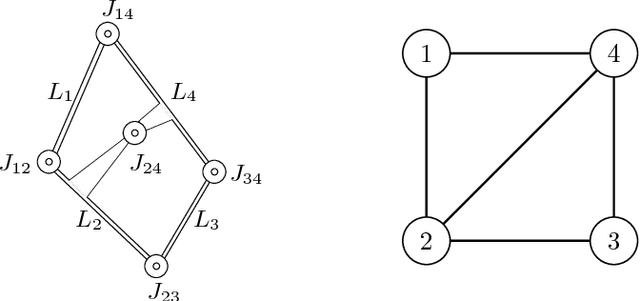
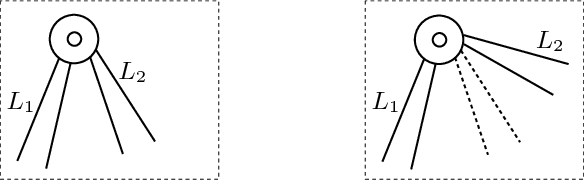
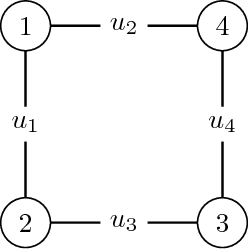
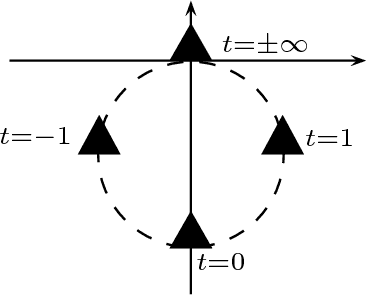
Designing mechanical devices, called linkages, that draw a given plane curve has been a topic that interested engineers and mathematicians for hundreds of years, and recently also computer scientists. Already in 1876, Kempe proposed a procedure for solving the problem in full generality, but his constructions tend to be extremely complicated. We provide a novel algorithm that produces much simpler linkages, but works only for parametric curves. Our approach is to transform the problem into a factorization task over some noncommutative algebra. We show how to compute such a factorization, and how to use it to construct a linkage tracing a given curve.

A Technique for Deriving Equational Conditions on the Denavit-Hartenberg Parameters of 6R Linkages that are Necessary for Movability

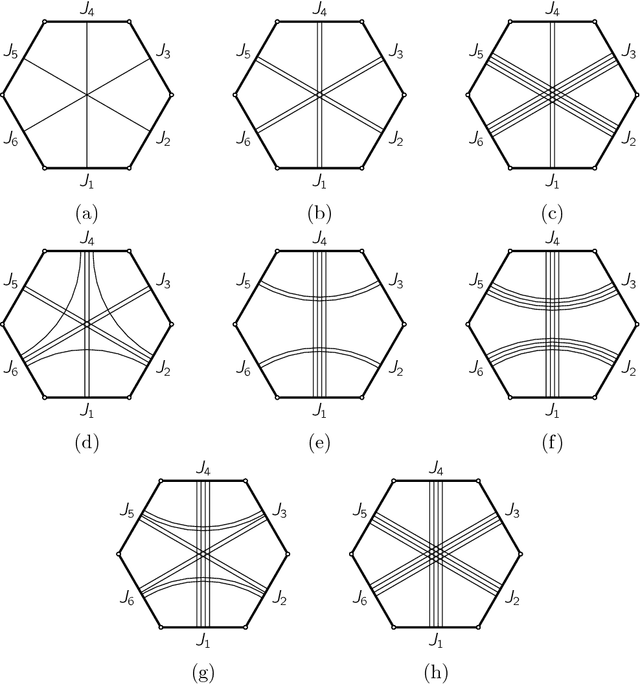
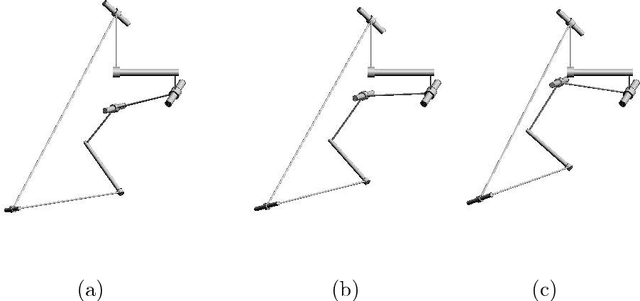
A closed 6R linkage is generically rigid. Special cases may be mobile. Many families of mobile 6R linkages have been characterised in terms of the invariant Denavit-Hartenberg parameters of the linkage. In other words, many sufficient conditions for mobility are known. In this paper we give, for the first time, equational conditions on the invariant Denavit-Hartenberg parameters that are necessary for mobility. The method is based on the theory of bonds. We illustrate the method by deriving the equational conditions for various well-known linkages (Bricard's line symmetric linkage, Hooke's linkage, Dietmaier's linkage, and recent a generalization of Bricard's orthogonal linkage), starting from their bond diagrams; and by deriving the equations for another bond diagram, thereby discovering a new mobile 6R linkage.

From the Fundamental Theorem of Algebra to Kempe's Universality Theorem

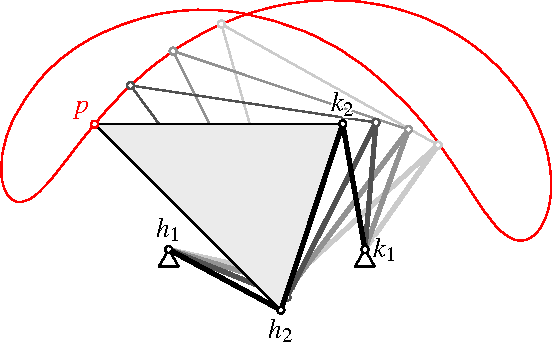
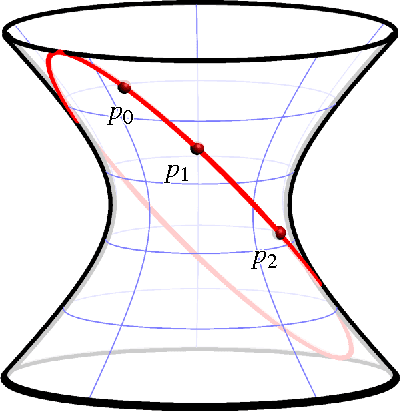
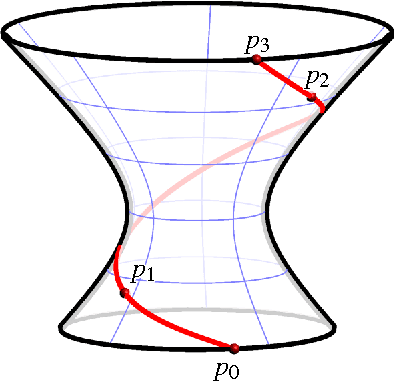
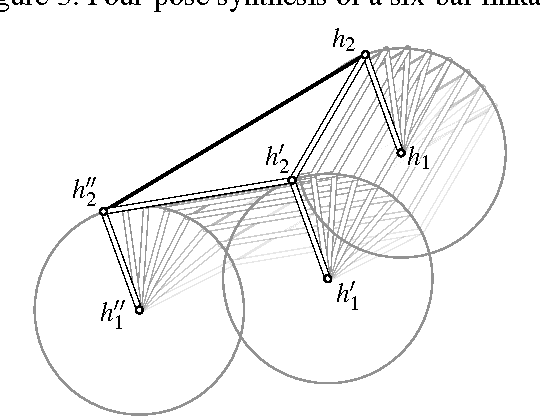
This article provides a gentle introduction for a general mathematical audience to the factorization theory of motion polynomials and its application in mechanism science. This theory connects in a rather unexpected way a seemingly abstract mathematical topic, the non-unique factorization of certain polynomials over the ring of dual quaternions, with engineering applications. Four years after its introduction, it is already clear how beneficial it has been to both fields.

7R Darboux Linkages by Factorization of Motion Polynomials

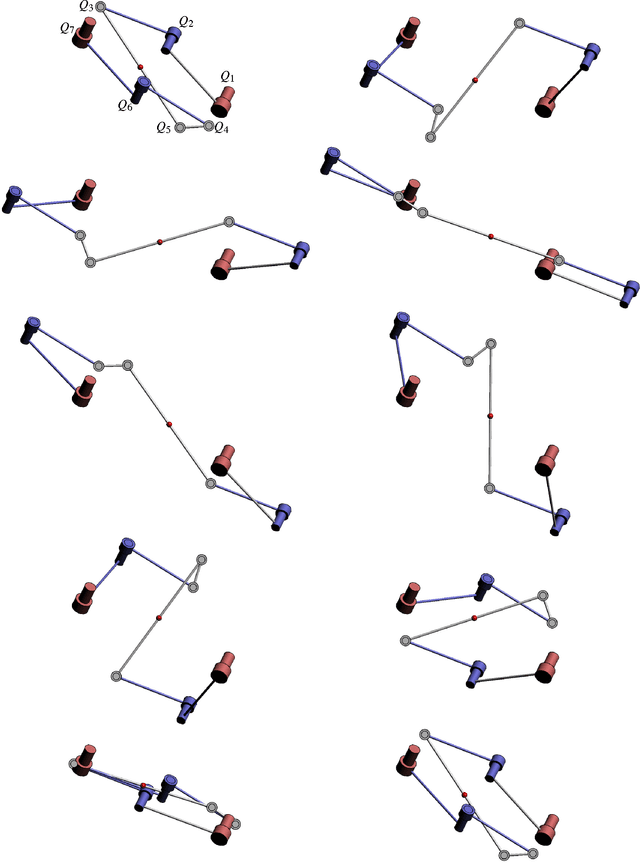
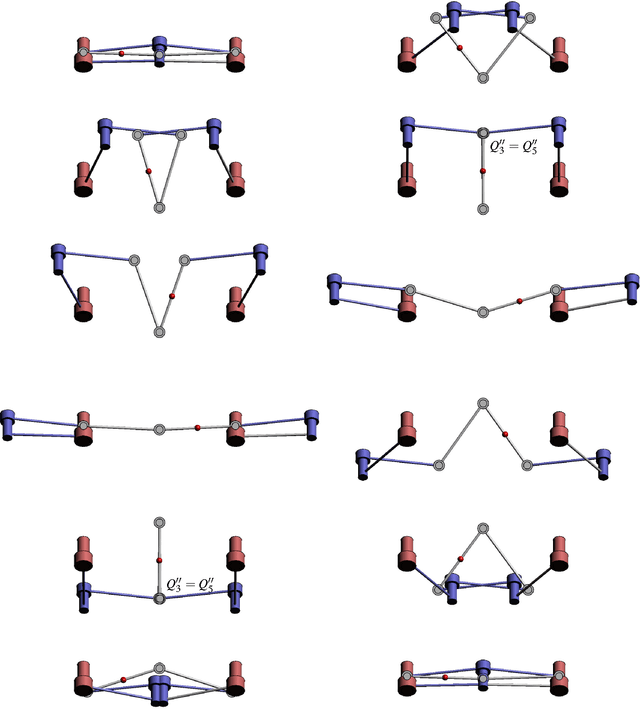
In this paper, we construct two types of 7R closed single loop linkages by combining different factorizations of a general (non-vertical) Darboux motion. These factorizations are obtained by extensions of a factorization algorithm for a generic rational motion. The first type of 7R linkages has several one-dimensional configuration components and one of them corresponds to the Darboux motion. The other type is a 7R linkage with two degrees of freedom and without one-dimensional component. The Darboux motion is a curve in an irreducible two dimensional configuration component.

Factorization of Rational Motions: A Survey with Examples and Applications

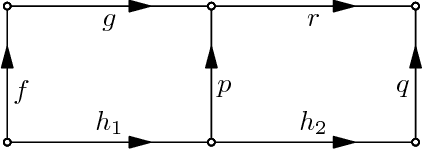
Since its introduction in 2012, the factorization theory for rational motions quickly evolved and found applications in theoretical and applied mechanism science. We provide an accessible introduction to motion factorization with many examples, summarize recent developments and hint at some new applications. In particular, we provide pseudo-code for the generic factorization algorithm, demonstrate how to find a replacement linkage for a special case in the synthesis of Bennett mechanisms and, as an example of non-generic factorization, synthesize open chains for circular and elliptic translations.

Factorization of Motion Polynomials

In this paper, we consider the existence of a factorization of a monic, bounded motion polynomial. We prove existence of factorizations, possibly after multiplication with a real polynomial and provide algorithms for computing polynomial factor and factorizations. The first algorithm is conceptually simpler but may require a high degree of the polynomial factor. The second algorithm gives an optimal degree.