A new line-symmetric mobile infinity-pod

We construct parallel manipulators with one degree of freedom and admitting infinitely many legs lying on a curve of degree ten and genus six. Our technique relies upon a duality between the spaces parametrizing all the possible legs and all the possible configurations of a manipulator. Before describing our construction, we show how this duality helps explaining several known phenomena regarding mobility of parallel manipulators.

Hexapods with a small linear span

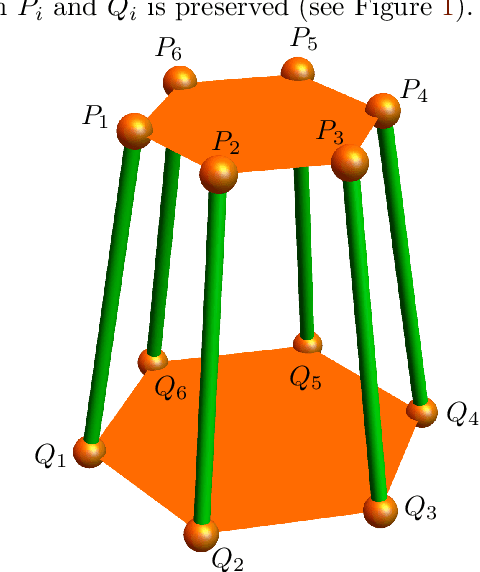
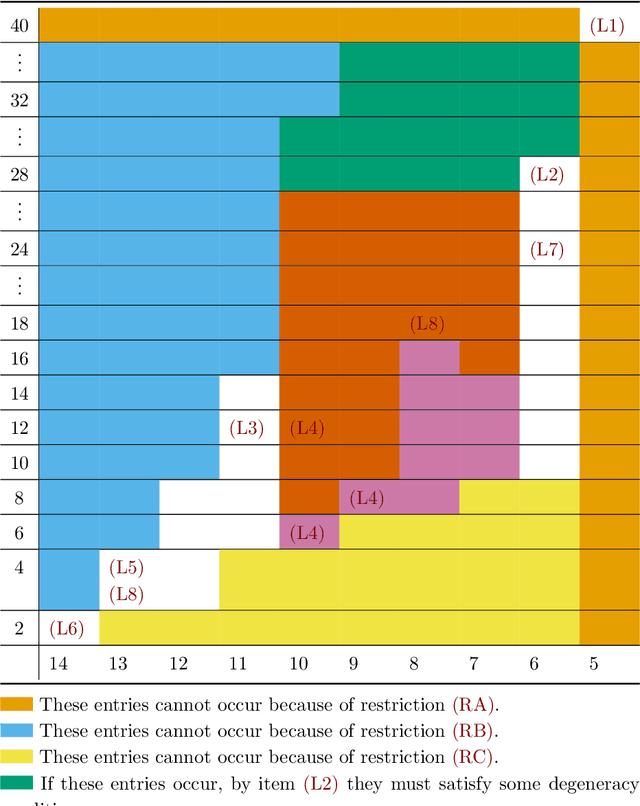
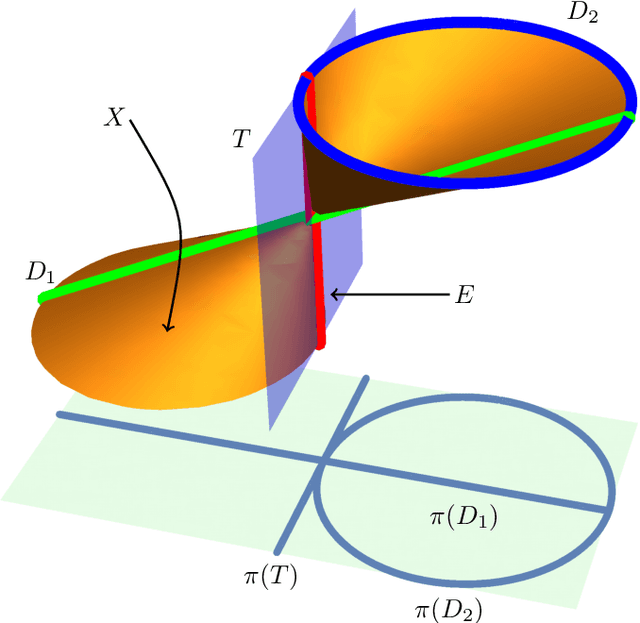
The understanding of mobile hexapods, i.e., parallel manipulators with six legs, is one of the driving questions in theoretical kinematics. We aim at contributing to this understanding by employing techniques from algebraic geometry. The set of configurations of a mobile hexapod with one degree of freedom has the structure of a projective curve, which hence has a degree and an embedding dimension. Our main result is a classification of configuration curves of hexapods that satisfy some restrictions on their embedding dimension.

On the existence of paradoxical motions of generically rigid graphs on the sphere

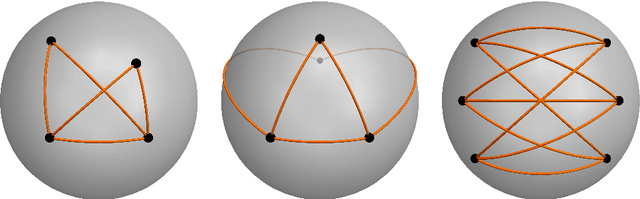
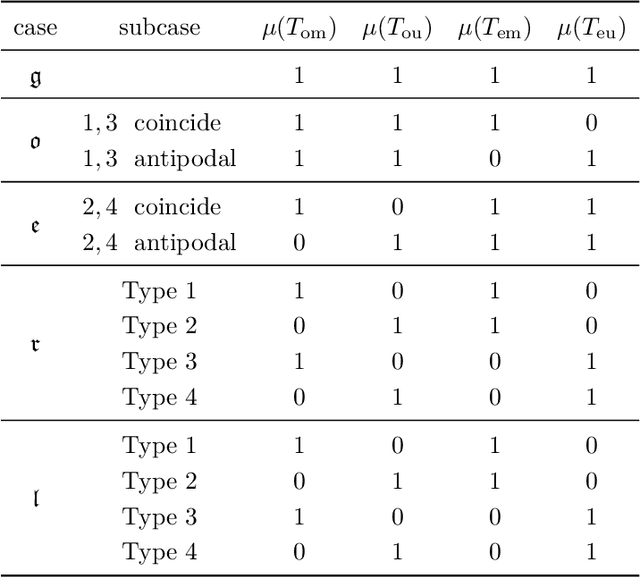
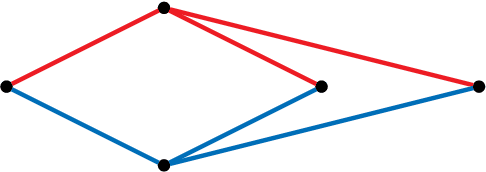
We interpret realizations of a graph on the sphere up to rotations as elements of a moduli space of curves of genus zero. We focus on those graphs that admit an assignment of edge lengths on the sphere resulting in a flexible object. Our interpretation of realizations allows us to provide a combinatorial characterization of these graphs in terms of the existence of particular colorings of the edges. Moreover, we determine necessary relations for flexibility between the spherical lengths of the edges. We conclude by classifying all possible motions on the sphere of the complete bipartite graph with $3+3$ vertices where no two vertices coincide or are antipodal.

Planar Linkages Following a Prescribed Motion

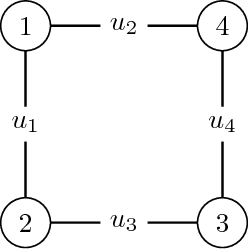
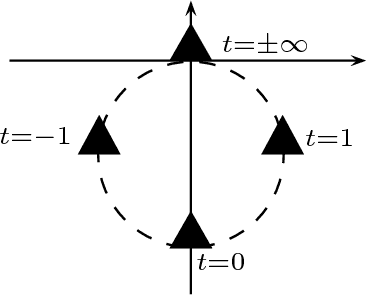
Designing mechanical devices, called linkages, that draw a given plane curve has been a topic that interested engineers and mathematicians for hundreds of years, and recently also computer scientists. Already in 1876, Kempe proposed a procedure for solving the problem in full generality, but his constructions tend to be extremely complicated. We provide a novel algorithm that produces much simpler linkages, but works only for parametric curves. Our approach is to transform the problem into a factorization task over some noncommutative algebra. We show how to compute such a factorization, and how to use it to construct a linkage tracing a given curve.

Mobile Icosapods

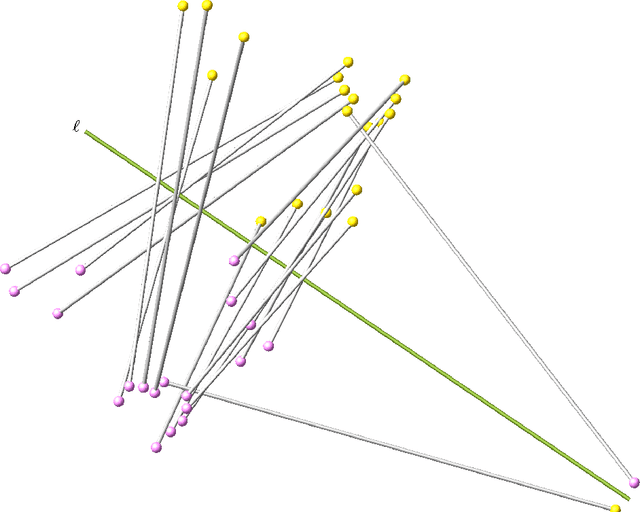
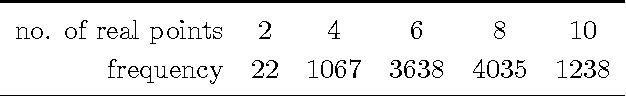
Pods are mechanical devices constituted of two rigid bodies, the base and the platform, connected by a number of other rigid bodies, called legs, that are anchored via spherical joints. It is possible to prove that the maximal number of legs of a mobile pod, when finite, is 20. In 1904, Borel designed a technique to construct examples of such 20-pods, but could not constrain the legs to have base and platform points with real coordinates. We show that Borel's construction yields all mobile 20-pods, and that it is possible to construct examples with all real coordinates.

Liaison Linkages

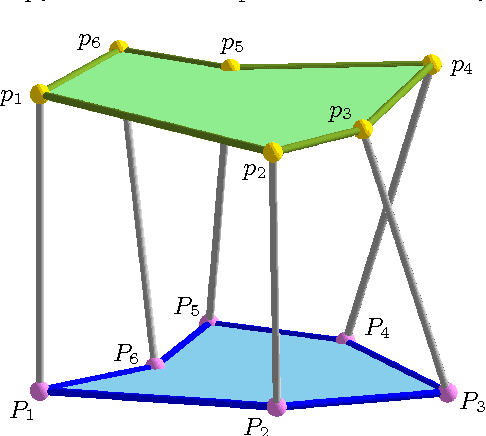
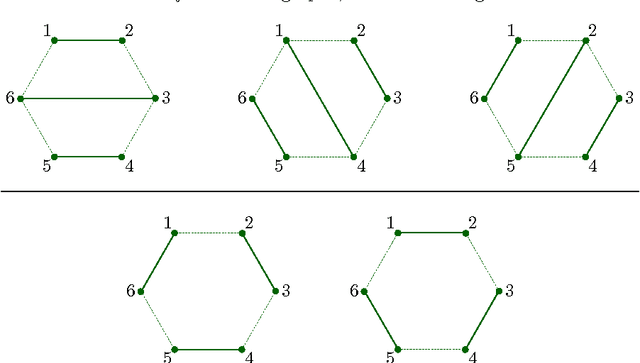
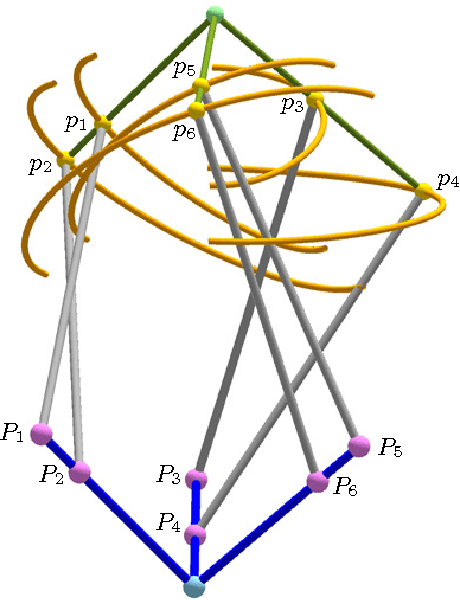
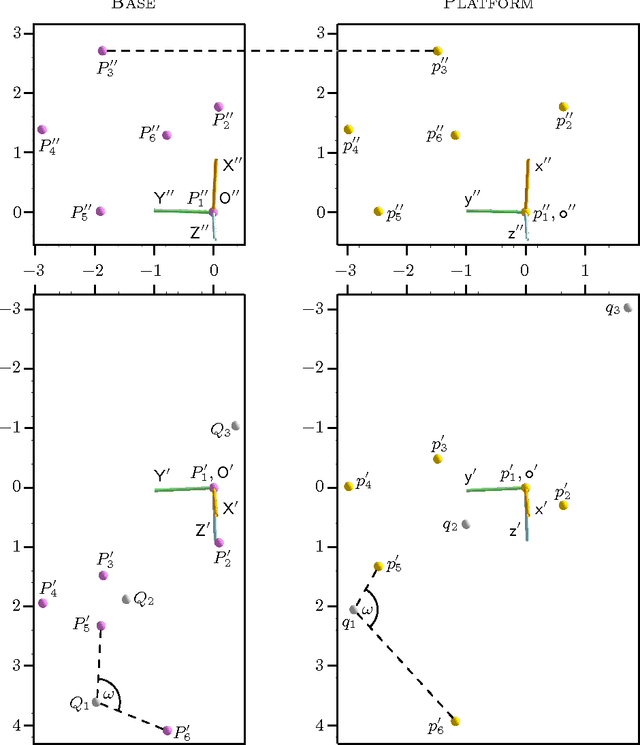
The complete classification of hexapods - also known as Stewart Gough platforms - of mobility one is still open. To tackle this problem, we can associate to each hexapod of mobility one an algebraic curve, called the configuration curve. In this paper we establish an upper bound for the degree of this curve, assuming the hexapod is general enough. Moreover, we provide a construction of hexapods with curves of maximal degree, which is based on liaison, a technique used in the theory of algebraic curves.

Möbius Photogrammetry

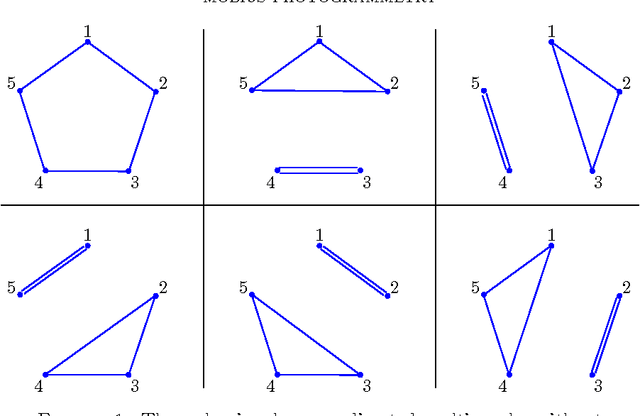
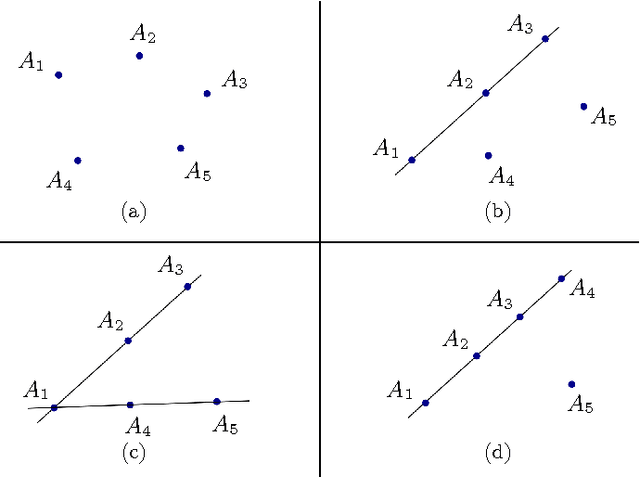
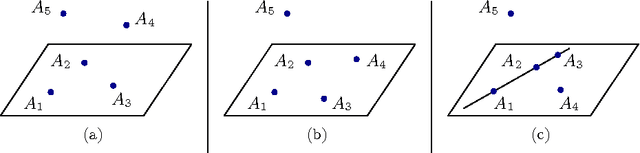
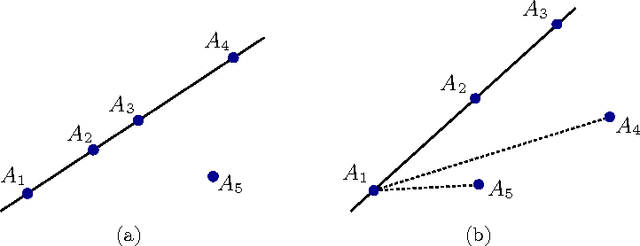
Motivated by results on the mobility of mechanical devices called pentapods, this paper deals with a mathematically freestanding problem, which we call M\"obius Photogrammetry. Unlike traditional photogrammetry, which tries to recover a set of points in three-dimensional space from a finite set of central projection, we consider the problem of reconstructing a vector of points in $\mathbb{R}^3$ starting from its orthogonal parallel projections. Moreover, we assume that we have partial information about these projections, namely that we know them only up to M\"obius transformations. The goal in this case is to understand to what extent we can reconstruct the starting set of points, and to prove that the result can be achieved if we allow some uncertainties in the answer. Eventually, the techniques developed in the paper allow us to show that for a pentapod with mobility at least two either some anchor points are collinear, or platform and base are similar, or they are planar and affine equivalent.

Bond theory for pentapods and hexapods

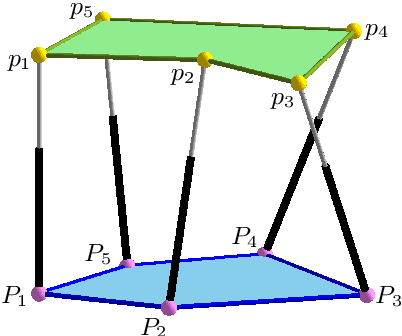
This paper deals with the old and classical problem of determining necessary conditions for the overconstrained mobility of some mechanical device. In particular, we show that the mobility of pentapods/hexapods implies either a collinearity condition on the anchor points, or a geometric condition on the normal projections of base and platform points. The method is based on a specific compactification of the group of direct isometries of $\mathbb{R}^3$.