Hexapods with a small linear span

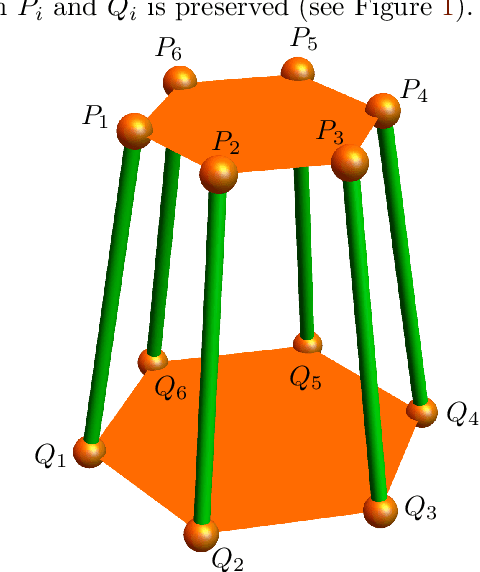
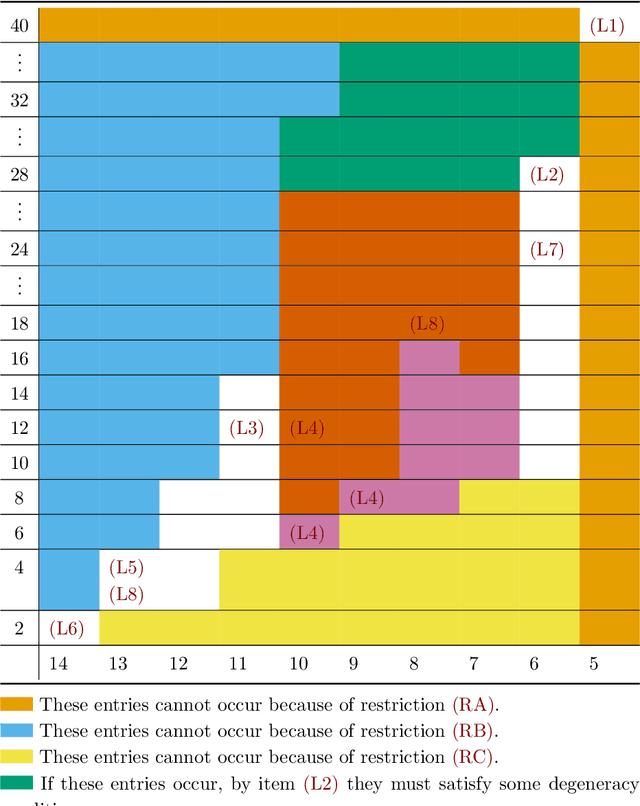
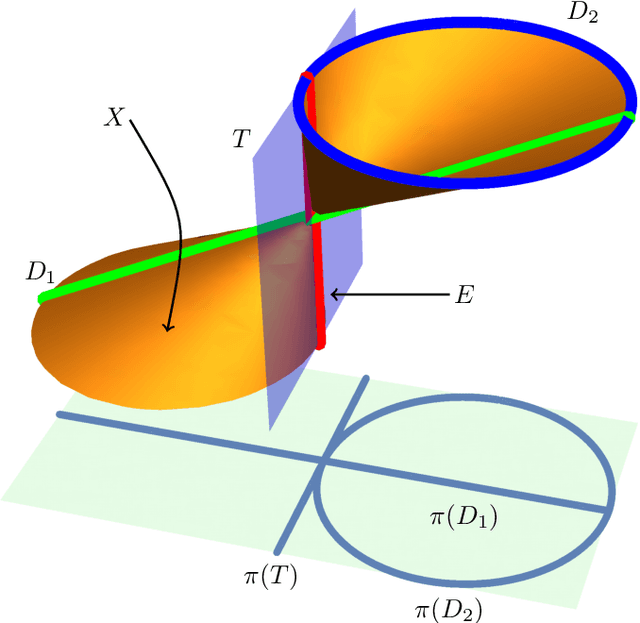
The understanding of mobile hexapods, i.e., parallel manipulators with six legs, is one of the driving questions in theoretical kinematics. We aim at contributing to this understanding by employing techniques from algebraic geometry. The set of configurations of a mobile hexapod with one degree of freedom has the structure of a projective curve, which hence has a degree and an embedding dimension. Our main result is a classification of configuration curves of hexapods that satisfy some restrictions on their embedding dimension.