Representing Piecewise Linear Functions by Functions with Small Arity

A piecewise linear function can be described in different forms: as an arbitrarily nested expression of $\min$- and $\max$-functions, as a difference of two convex piecewise linear functions, or as a linear combination of maxima of affine-linear functions. In this paper, we provide two main results: first, we show that for every piecewise linear function there exists a linear combination of $\max$-functions with at most $n+1$ arguments, and give an algorithm for its computation. Moreover, these arguments are contained in the finite set of affine-linear functions that coincide with the given function in some open set. Second, we prove that the piecewise linear function $\max(0, x_{1}, \ldots, x_{n})$ cannot be represented as a linear combination of maxima of less than $n+1$ affine-linear arguments. This was conjectured by Wang and Sun in 2005 in a paper on representations of piecewise linear functions as linear combination of maxima.

A new line-symmetric mobile infinity-pod

We construct parallel manipulators with one degree of freedom and admitting infinitely many legs lying on a curve of degree ten and genus six. Our technique relies upon a duality between the spaces parametrizing all the possible legs and all the possible configurations of a manipulator. Before describing our construction, we show how this duality helps explaining several known phenomena regarding mobility of parallel manipulators.

Classification of Higher Mobility Linkages

We provide a complete classification of paradoxical $n$-linkages, $n\geq6$ whose mobility is $n-4$ or higher containing $R$, $P$ or $H$ joints. We also explicitly write down strong necessary conditions for $nR$-linkages of mobility $n-5$.

Hexapods with a small linear span

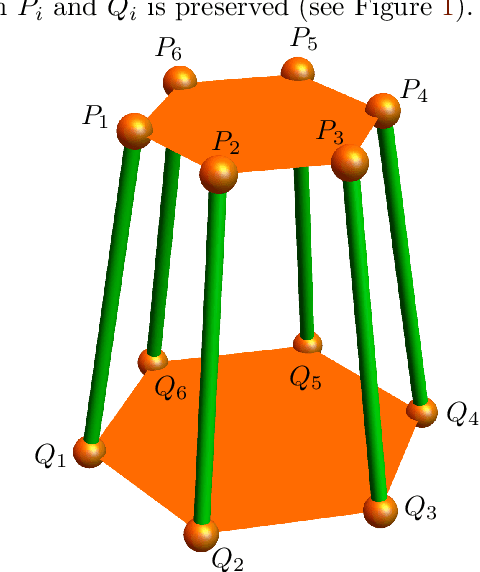
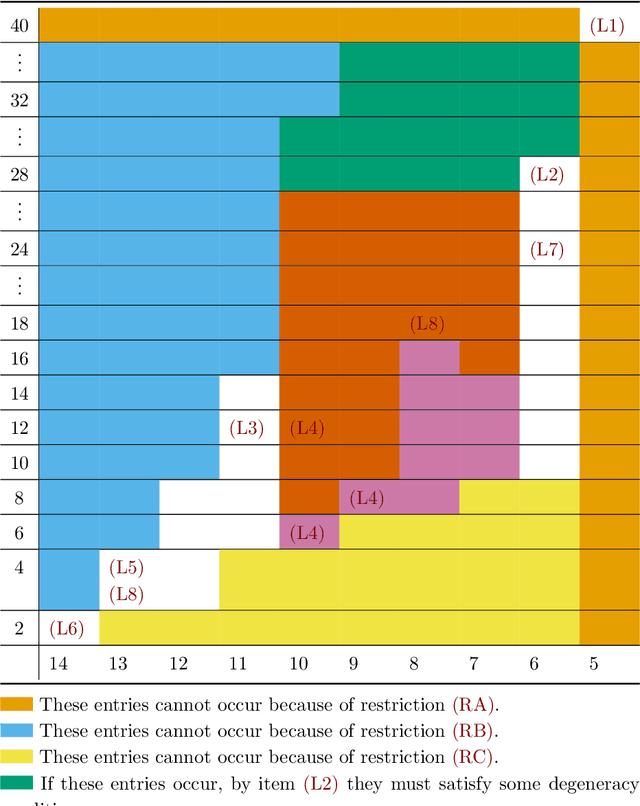
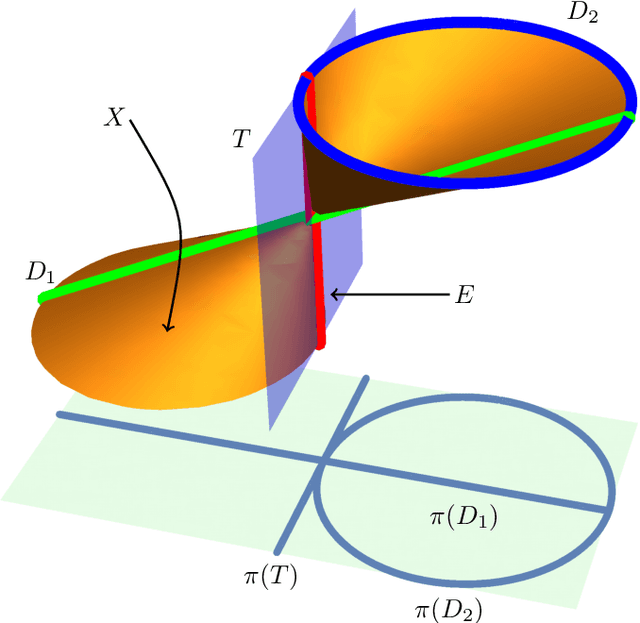
The understanding of mobile hexapods, i.e., parallel manipulators with six legs, is one of the driving questions in theoretical kinematics. We aim at contributing to this understanding by employing techniques from algebraic geometry. The set of configurations of a mobile hexapod with one degree of freedom has the structure of a projective curve, which hence has a degree and an embedding dimension. Our main result is a classification of configuration curves of hexapods that satisfy some restrictions on their embedding dimension.

On the Classification of Motions of Paradoxically Movable Graphs

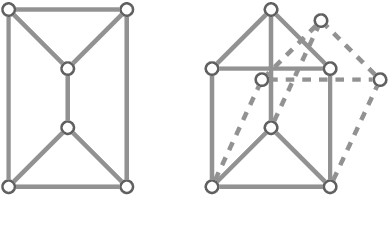
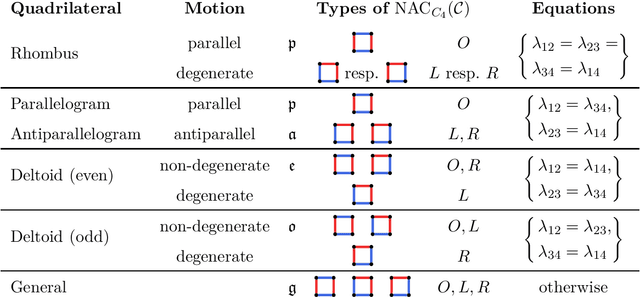
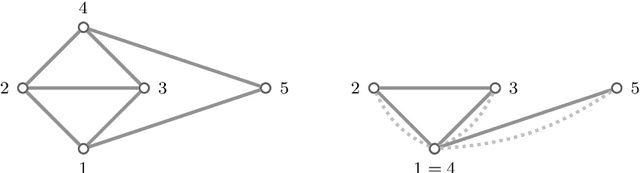
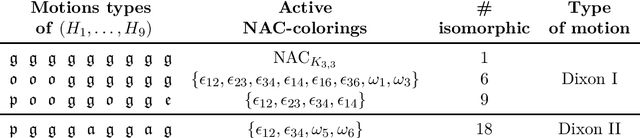
Edge lengths of a graph are called flexible if there exist infinitely many non-congruent realizations of the graph in the plane satisfying these edge lengths. It has been shown recently that a graph has flexible edge lengths if and only if the graph has a special type of edge coloring called NAC-coloring. We address the question how to determine all possible proper flexible edge lengths from the set of all NAC-colorings of a graph. We do so using restrictions to 4-cycle subgraphs.

On the existence of paradoxical motions of generically rigid graphs on the sphere

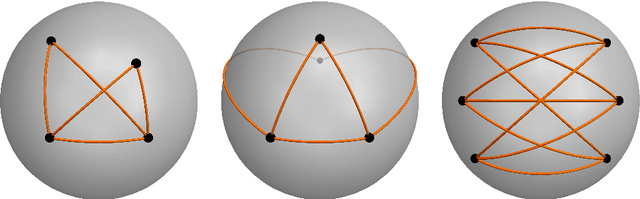
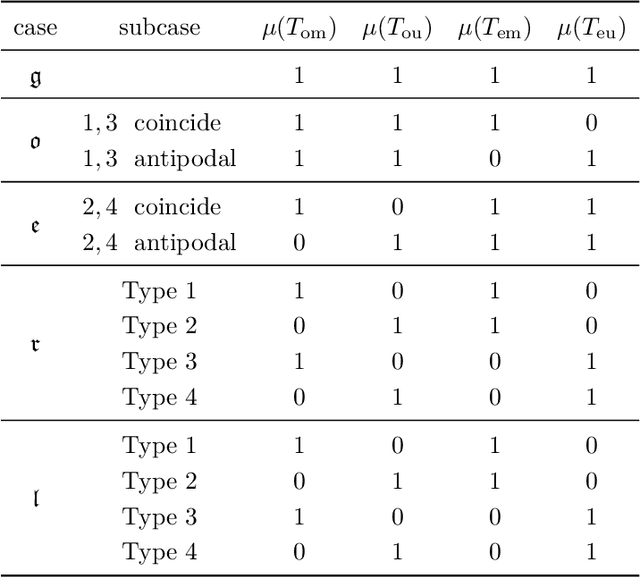
We interpret realizations of a graph on the sphere up to rotations as elements of a moduli space of curves of genus zero. We focus on those graphs that admit an assignment of edge lengths on the sphere resulting in a flexible object. Our interpretation of realizations allows us to provide a combinatorial characterization of these graphs in terms of the existence of particular colorings of the edges. Moreover, we determine necessary relations for flexibility between the spherical lengths of the edges. We conclude by classifying all possible motions on the sphere of the complete bipartite graph with $3+3$ vertices where no two vertices coincide or are antipodal.

Kempe's Universality Theorem for Rational Space Curves

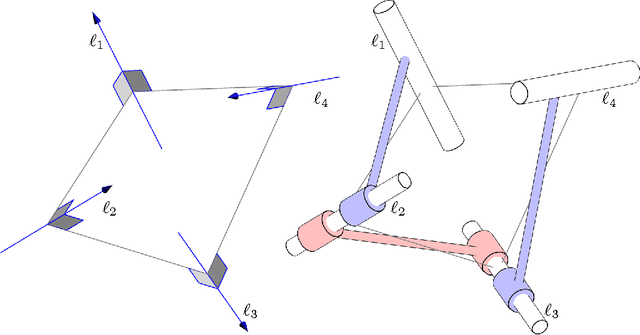
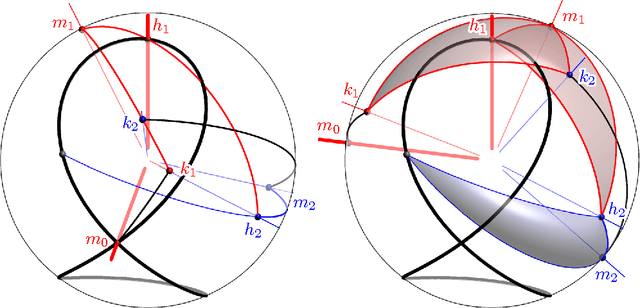
We prove that every bounded rational space curve of degree d and circularity c can be drawn by a linkage with 9/2 d - 6c + 1 revolute joints. Our proof is based on two ingredients. The first one is the factorization theory of motion polynomials. The second one is the construction of a motion polynomial of minimum degree with given orbit. Our proof also gives the explicity construction of the linkage.

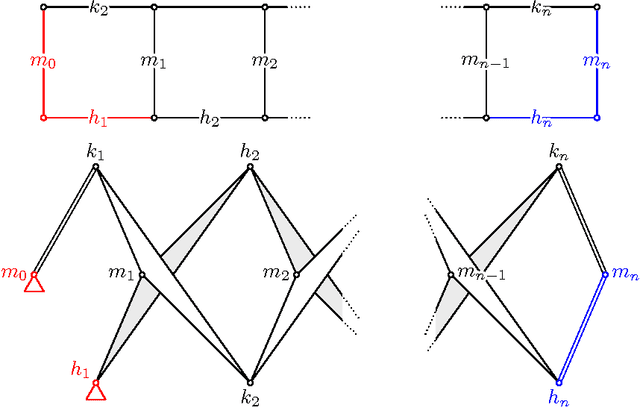
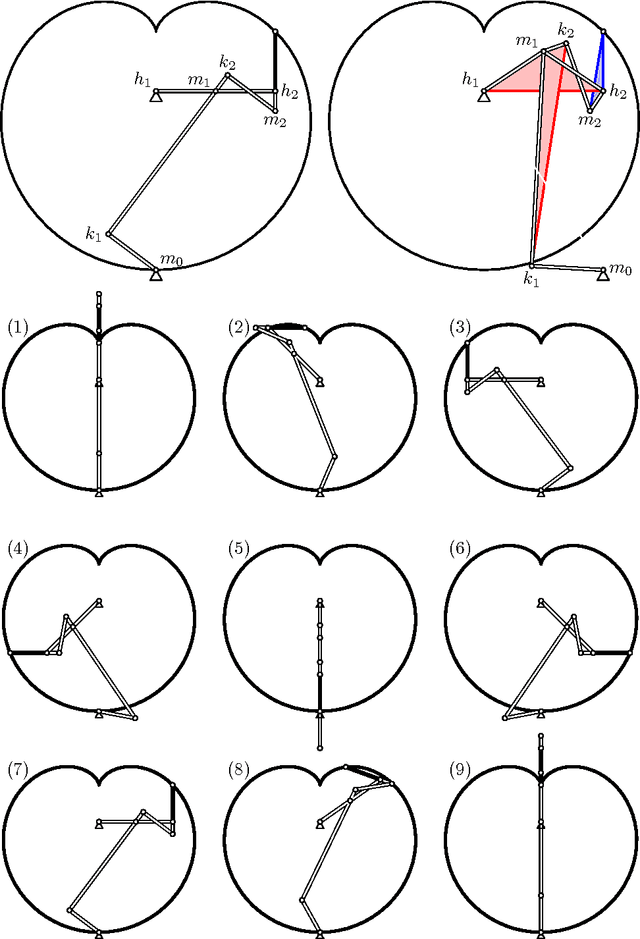
Planar Linkages Following a Prescribed Motion

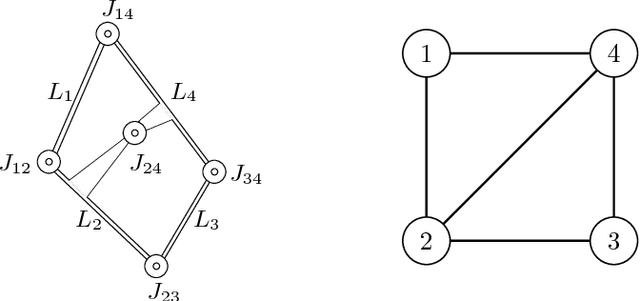
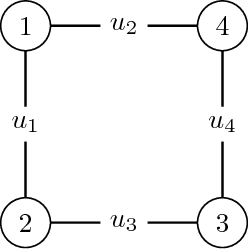
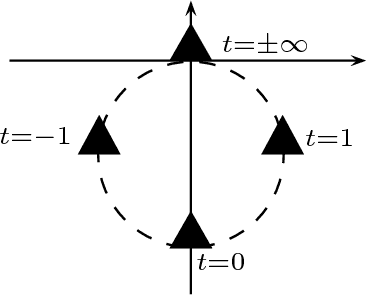
Designing mechanical devices, called linkages, that draw a given plane curve has been a topic that interested engineers and mathematicians for hundreds of years, and recently also computer scientists. Already in 1876, Kempe proposed a procedure for solving the problem in full generality, but his constructions tend to be extremely complicated. We provide a novel algorithm that produces much simpler linkages, but works only for parametric curves. Our approach is to transform the problem into a factorization task over some noncommutative algebra. We show how to compute such a factorization, and how to use it to construct a linkage tracing a given curve.

Mobile Icosapods

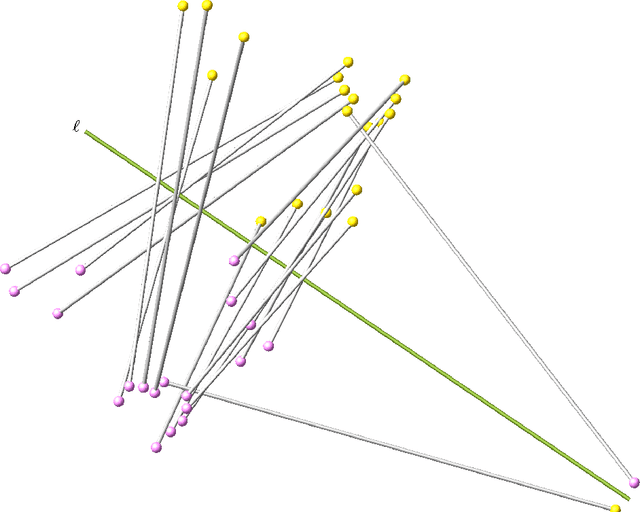
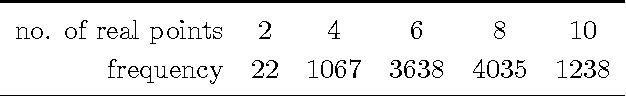
Pods are mechanical devices constituted of two rigid bodies, the base and the platform, connected by a number of other rigid bodies, called legs, that are anchored via spherical joints. It is possible to prove that the maximal number of legs of a mobile pod, when finite, is 20. In 1904, Borel designed a technique to construct examples of such 20-pods, but could not constrain the legs to have base and platform points with real coordinates. We show that Borel's construction yields all mobile 20-pods, and that it is possible to construct examples with all real coordinates.

Addendum to Pentapods with Mobility 2

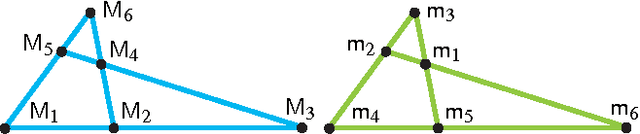
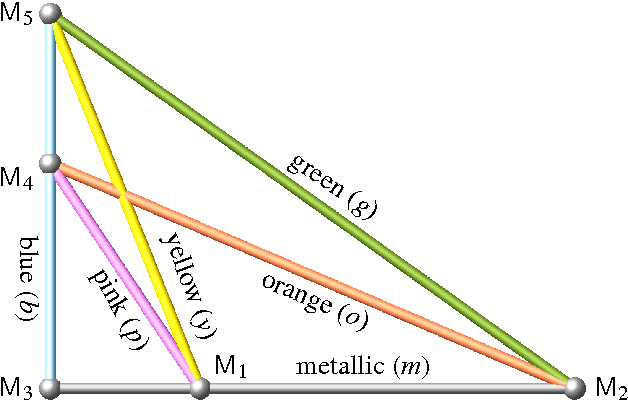
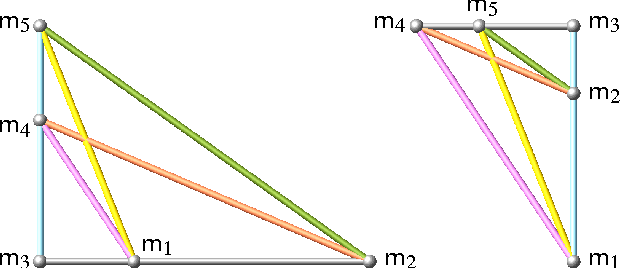
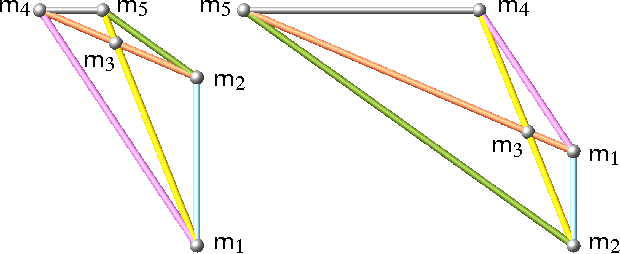
In a foregoing publication the authors studied pentapods with mobility 2, where neither all platform anchor points nor all base anchor points are located on a line. It turned out that the given classification is incomplete. This addendum is devoted to the discussion of the missing cases resulting in additional solutions already known to Duporcq.