A global approach for the redefinition of higher-order flexibility and rigidity

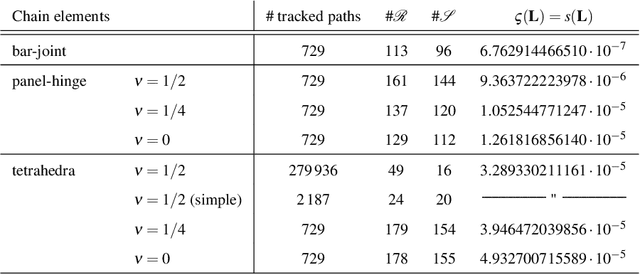
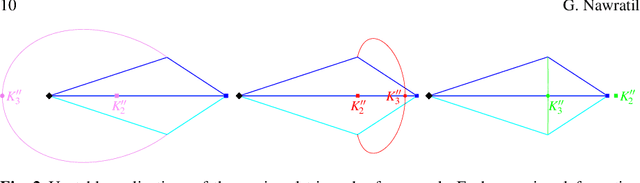
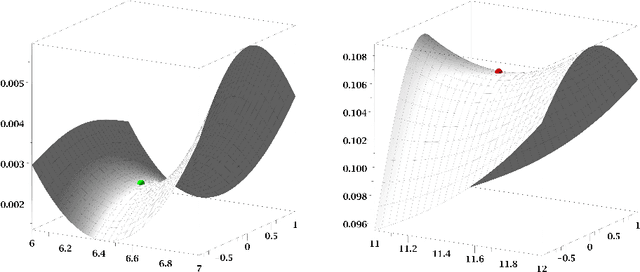
The famous example of the double-Watt mechanism given by Connelly and Servatius raises some problems concerning the classical definitions of higher-order flexibility and rigidity, respectively, as they attest the cusp configuration of the mechanism a third-order rigidity, which conflicts with its continuous flexion. Some attempts were done to resolve the dilemma but they could not settle the problem. As cusp mechanisms demonstrate the basic shortcoming of any local mobility analysis using higher-order constraints, we present a global approach inspired by Sabitov's finite algorithm for testing the bendability of a polyhedron, which allows us (a) to compute iteratively configurations with a higher-order flexion and (b) to come up with a proper redefinition of higher-order flexibility and rigidity. We also give algorithms for computing the flexion orders as well as the associated flexes. The presented approach is demonstrated on several examples (double-Watt mechanisms and Tarnai's Leonardo structure). Moreover, we determine all configurations of a given 3-RPR manipulator with a third-order flexion and present a corresponding joint-bar framework of flexion order 23.

From axial C-hedra to general P-nets

We give a full classification of continuous flexible discrete axial cone-nets, which are called axial C-hedra. The obtained result can also be used to construct their semi-discrete analogs. Moreover, we identify a novel subclass within the determined class of (semi-)discrete axial cone-nets, whose members are named axial P-nets as they fulfill the proportion (P) of the intercept theorem. Known special cases of these axial P-nets are the smooth and discrete conic crease patterns with reflecting rule lines. By using a parallelism operation one can even generalize axial P-nets. The resulting general P-nets constitute a rich novel class of continuous flexible (semi-)discrete surfaces, which allow direct access to their spatial shapes by three control polylines. This intuitive method makes them suitable for transformable design tasks using interactive tools.

Architecture Singularity Distance Computations for Linear Pentapods

The kinematic/robotic community is not only interested in measuring the closeness of a given robot configuration to its next singular one but also in a geometric meaningful index evaluating how far the robot design is away from being architecturally singular. Such an architecture singularity distance, which can be used by engineers as a criterion within the design process, is presented for a certain class of parallel manipulators of Stewart-Gough type; namely so-called linear pentapods. Geometrically the architecture singular designs are well-understood and can be subclassified into several cases, which allows to solve the optimization problem of computing the closest architecture singular design to a given linear pentapod with algorithms from numerical algebraic geometry.

Singularity Distance Computations of 3-RPR Manipulators Using Intrinsic Metrics

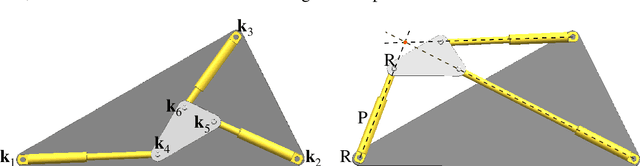
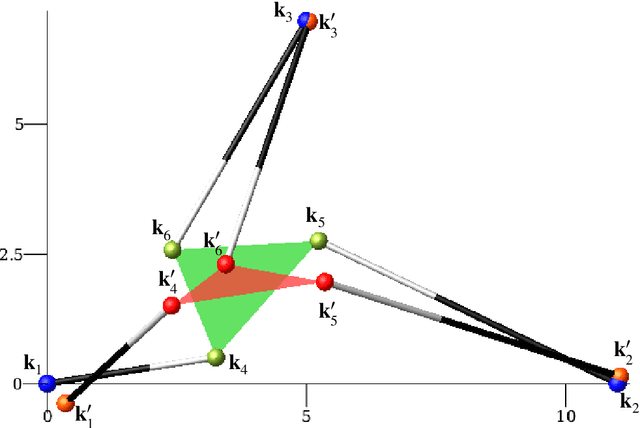
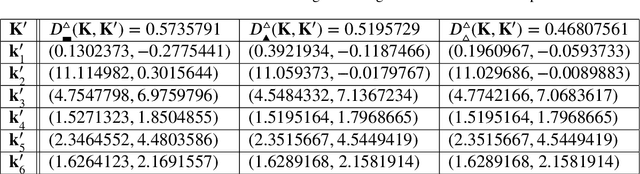
We present an efficient algorithm for computing the closest singular configuration to each non-singular pose of a 3-RPR planar manipulator performing a 1-parametric motion. By considering a 3-RPR manipulator as a planar framework, one can use methods from rigidity theory to compute the singularity distance with respect to an intrinsic metric. There are different design options as the platform/base can be seen as a triangular plate or as a pin-jointed triangular bar structure. Moreover, we also allow the additional possibility of pinning down the base/platform triangle to the fixed/moving system thus it cannot be deformed. For the resulting nine interpretations, we compute the corresponding intrinsic metrics based on the total elastic strain energy density of the framework using the physical concept of Green-Lagrange strain. The global optimization problem of finding the closest singular configuration with respect to these metrics is solved by using tools from numerical algebraic geometry. The proposed algorithm is demonstrated based on an example.

Singularity Distance Computations for 3-RPR Manipulators using Extrinsic Metrics

It is well-known that parallel manipulators are prone to singularities. There is still a lack of distance evaluation functions, referred to as metrics, for computing the distance between two 3-RPR configurations. The presented extrinsic metrics take the combinatorial structure of the manipulator into account as well as different design options. Using these extrinsic metrics, we formulate constrained optimization problems, which aim to find the closest singular configurations for a given non-singular configuration. The solution of the corresponding system of polynomial equations relies on algorithms from numerical algebraic geometry implemented in the software package Bertini. Moreover, we developed a computational pipeline for computing the singularity distance along a 1-parametric motion of the manipulator. To facilitate these computations for the user, an open-source interface is developed between software packages Maple, Bertini, and Paramotopy. The presented approach is demonstrated based on a numerical example.

Snappability and singularity-distance of pin-jointed body-bar frameworks

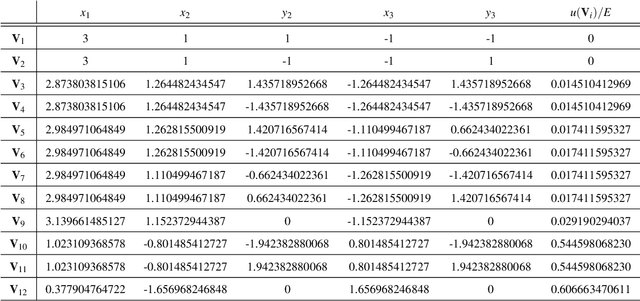
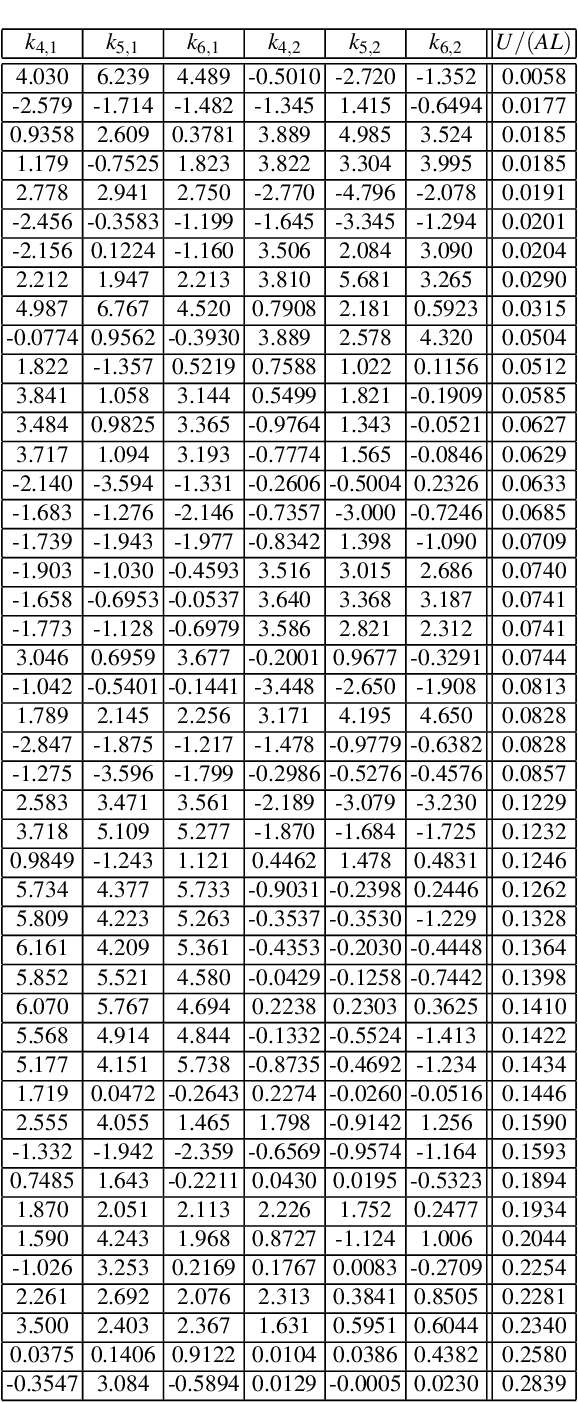
It is well-known that there exist rigid frameworks whose physical models can snap between different realizations due to non-destructive elastic deformations of material. We present a method to measure these snapping capability based on the total elastic strain energy density of the framework by using the physical concept of Green-Lagrange strain. As this so-called snappability only depends on the intrinsic framework geometry, it enables a fair comparison of pin-jointed body-bar frameworks, thus it can serve engineers as a criterion within the design process either to avoid snapping phenomena (e.g. truss structures) or to utilize them (e.g. multistable materials). Moreover, it turns out that the value obtained from this intrinsic pseudometric also gives the distance to the closest shaky configuration in the case of isostatic frameworks. Therefore it is also of use for the kinematics community, which is highly interested in the computation of these singularity-distances for diverse mechanical devices. In more detail we study this problem for parallel manipulators of Stewart-Gough type.

On the snappability and singularity-distance of frameworks with bars and triangular plates

In a recent article the author presented a method to measure the snapping capability -- shortly called snappability -- of bar-joint frameworks based on the total elastic strain energy by computing the deformation of all bars using Hooke's law and the definition of Cauchy/Engineering strain. Within the paper at hand, we extend this approach to frameworks composed of bars and triangular plates by using the physical concept of Green-Lagrange strain. An intrinsic pseudometric based on the resulting total elastic strain energy density cannot only be used for evaluating the snappability but also for measuring the distance to the closest singular configuration. The presented methods are demonstrated on the basis of the 3-legged planar parallel manipulator.

Evaluating the snappability of bar-joint frameworks

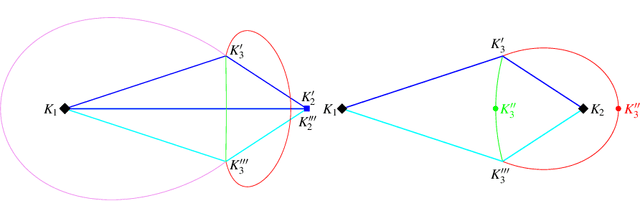
It is well-known that there exist bar-joint frameworks (without continuous flexions) whose physical models can snap between different realizations due to non-destructive elastic deformations of material. We present a method to measure these snapping capability -- shortly called snappability -- based on the total elastic strain energy of the framework by computing the deformation of all bars using Hook's law. The presented theoretical results give further connections between shakiness and snapping beside the well-known technique of averaging and deaveraging.

Variational Path Optimization of Linear Pentapods with a Simple Singularity Variety

The class of linear pentapods with a simple singularity variety is obtained by imposing architectural restrictions on the design in such a way that the manipulators singularity variety is linear in orientation position variables. It turns out that such simplification leads to crucial computational advantages while maintaining the machines applications in some fundamental industrial tasks such as five axis milling and laser cutting. We assume that a path between a given start and end pose of the end effector is known which is singularity free and within the manipulators workspace. An optimization process of the initial path is proposed in such a way that the parallel robot increases its distance to the singularity loci while the motion is being smoothed. In our case the computation time of the optimization is improved as we are dealing with pentapods having simple singularity varieties allowing a closed form solution for the local exterma of the singularity distance function. Formally this process is called variational path optimization which is the systematic optimization of a path by manipulating its variations of energy and distance to the obstacle which in this case is the singularity variety. In this process some physical limits of the mechanical joints are also taken into account.

Linear Pentapods with a Simple Singularity Variety

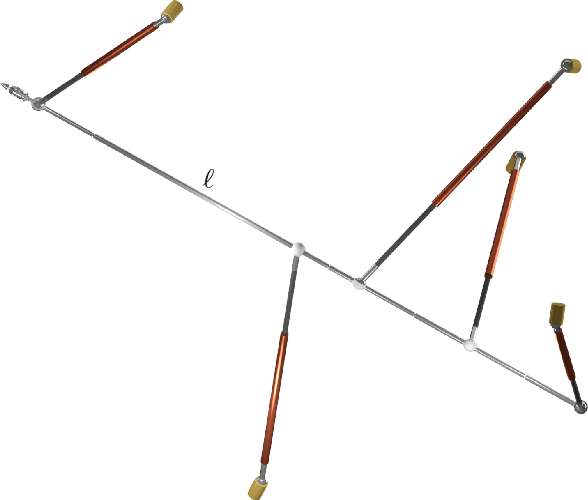
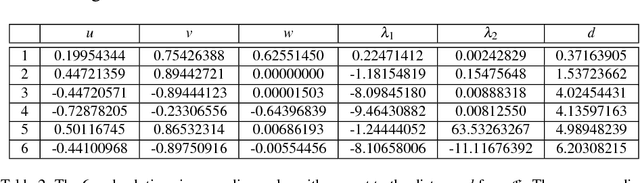
There exists a bijection between the configuration space of a linear pentapod and all points $(u,v,w,p_x,p_y,p_z)\in\mathbb{R}^{6}$ located on the singular quadric $\Gamma: u^2+v^2+w^2=1$, where $(u,v,w)$ determines the orientation of the linear platform and $(p_x,p_y,p_z)$ its position. Then the set of all singular robot configurations is obtained by intersecting $\Gamma$ with a cubic hypersurface $\Sigma$ in $\mathbb{R}^{6}$, which is only quadratic in the orientation variables and position variables, respectively. This article investigates the restrictions to be imposed on the design of this mechanism in order to obtain a reduction in degree. In detail we study the cases where $\Sigma$ is (1) linear in position variables, (2) linear in orientation variables and (3) quadratic in total. The resulting designs of linear pentapods have the advantage of considerably simplified computation of singularity-free spheres in the configuration space. Finally we propose three kinematically redundant designs of linear pentapods with a simple singularity surface.