Linear Pentapods with a Simple Singularity Variety
Paper and Code
Dec 19, 2017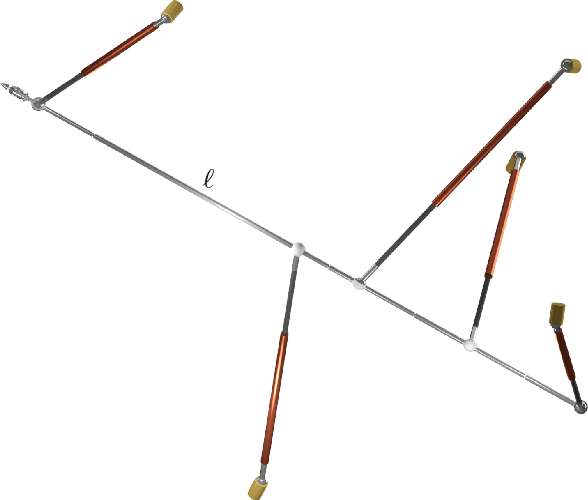


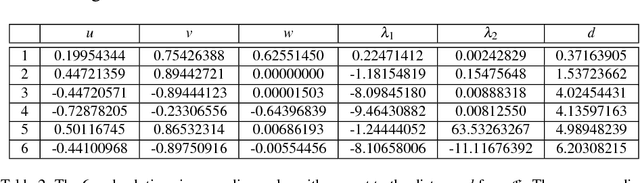
There exists a bijection between the configuration space of a linear pentapod and all points $(u,v,w,p_x,p_y,p_z)\in\mathbb{R}^{6}$ located on the singular quadric $\Gamma: u^2+v^2+w^2=1$, where $(u,v,w)$ determines the orientation of the linear platform and $(p_x,p_y,p_z)$ its position. Then the set of all singular robot configurations is obtained by intersecting $\Gamma$ with a cubic hypersurface $\Sigma$ in $\mathbb{R}^{6}$, which is only quadratic in the orientation variables and position variables, respectively. This article investigates the restrictions to be imposed on the design of this mechanism in order to obtain a reduction in degree. In detail we study the cases where $\Sigma$ is (1) linear in position variables, (2) linear in orientation variables and (3) quadratic in total. The resulting designs of linear pentapods have the advantage of considerably simplified computation of singularity-free spheres in the configuration space. Finally we propose three kinematically redundant designs of linear pentapods with a simple singularity surface.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge