Variational Path Optimization of Linear Pentapods with a Simple Singularity Variety

The class of linear pentapods with a simple singularity variety is obtained by imposing architectural restrictions on the design in such a way that the manipulators singularity variety is linear in orientation position variables. It turns out that such simplification leads to crucial computational advantages while maintaining the machines applications in some fundamental industrial tasks such as five axis milling and laser cutting. We assume that a path between a given start and end pose of the end effector is known which is singularity free and within the manipulators workspace. An optimization process of the initial path is proposed in such a way that the parallel robot increases its distance to the singularity loci while the motion is being smoothed. In our case the computation time of the optimization is improved as we are dealing with pentapods having simple singularity varieties allowing a closed form solution for the local exterma of the singularity distance function. Formally this process is called variational path optimization which is the systematic optimization of a path by manipulating its variations of energy and distance to the obstacle which in this case is the singularity variety. In this process some physical limits of the mechanical joints are also taken into account.

Linear Pentapods with a Simple Singularity Variety

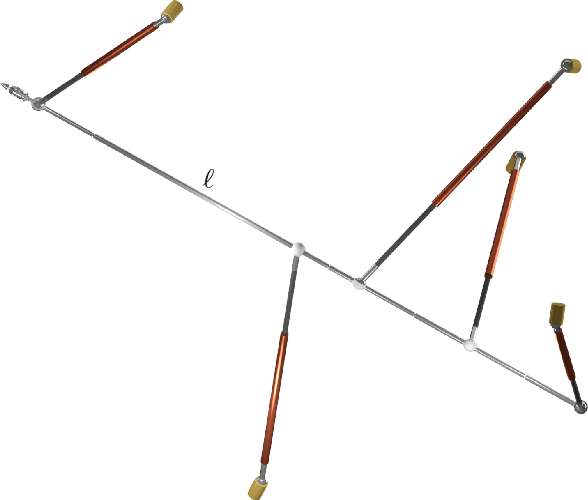
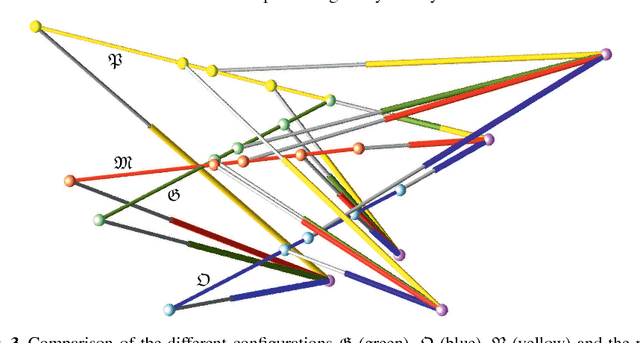
There exists a bijection between the configuration space of a linear pentapod and all points $(u,v,w,p_x,p_y,p_z)\in\mathbb{R}^{6}$ located on the singular quadric $\Gamma: u^2+v^2+w^2=1$, where $(u,v,w)$ determines the orientation of the linear platform and $(p_x,p_y,p_z)$ its position. Then the set of all singular robot configurations is obtained by intersecting $\Gamma$ with a cubic hypersurface $\Sigma$ in $\mathbb{R}^{6}$, which is only quadratic in the orientation variables and position variables, respectively. This article investigates the restrictions to be imposed on the design of this mechanism in order to obtain a reduction in degree. In detail we study the cases where $\Sigma$ is (1) linear in position variables, (2) linear in orientation variables and (3) quadratic in total. The resulting designs of linear pentapods have the advantage of considerably simplified computation of singularity-free spheres in the configuration space. Finally we propose three kinematically redundant designs of linear pentapods with a simple singularity surface.

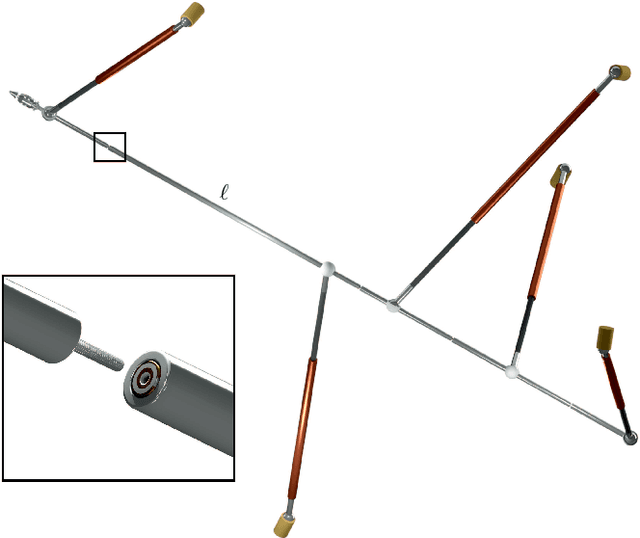
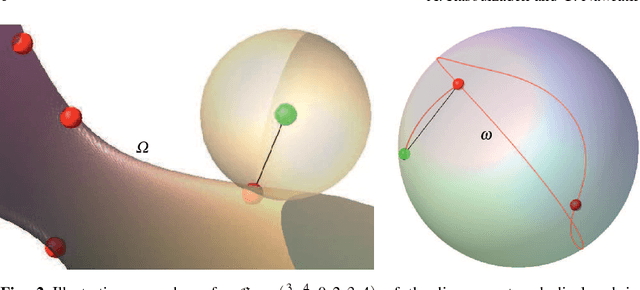
Rational Parametrization of Linear Pentapod's Singularity Variety and the Distance to it

A linear pentapod is a parallel manipulator with five collinear anchor points on the motion platform (end-effector), which are connected via extendible legs to the base. This manipulator has five controllable degrees-of-freedom and the remaining one is a free rotation around the motion platform axis (which in fact is an axial spindle). In this paper we present a rational parametrization of the singularity variety of the linear pentapod. Moreover we compute the shortest distance to this rational variety with respect to a suitable metric. Kinematically this distance can be interpreted as the radius of the maximal singularity free-sphere.

Kinematically Redundant Octahedral Motion Platform for Virtual Reality Simulations

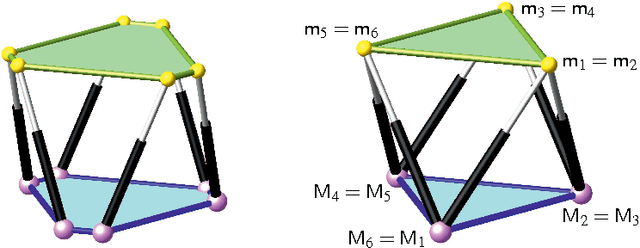
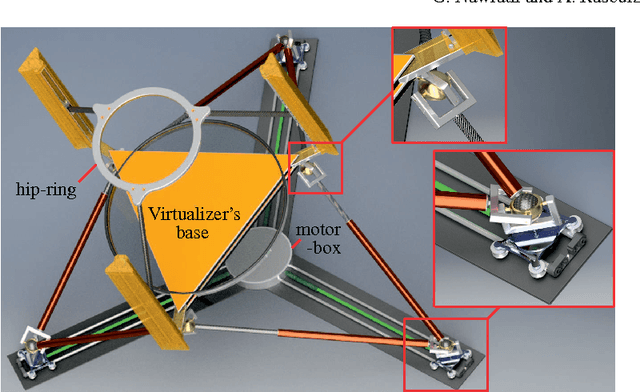
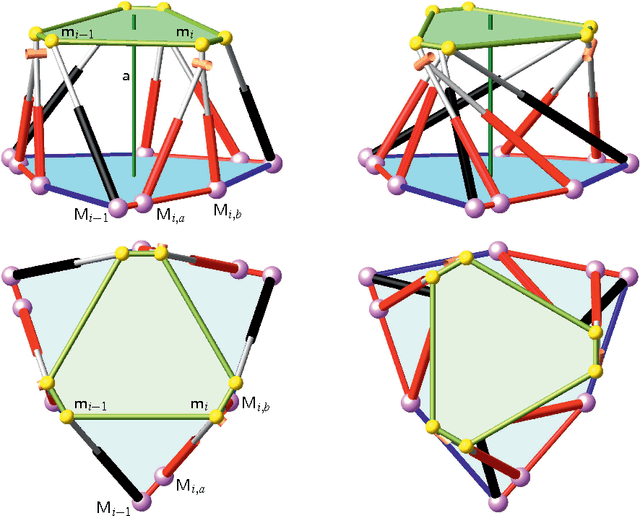
We propose a novel design of a parallel manipulator of Stewart Gough type for virtual reality application of single individuals; i.e. an omni-directional treadmill is mounted on the motion platform in order to improve VR immersion by giving feedback to the human body. For this purpose we modify the well-known octahedral manipulator in a way that it has one degree of kinematical redundancy; namely an equiform reconfigurability of the base. The instantaneous kinematics and singularities of this mechanism are studied, where especially "unavoidable singularities" are characterized. These are poses of the motion platform, which can only be realized by singular configurations of the mechanism despite its kinematic redundancy.