Architecture Singularity Distance Computations for Linear Pentapods

The kinematic/robotic community is not only interested in measuring the closeness of a given robot configuration to its next singular one but also in a geometric meaningful index evaluating how far the robot design is away from being architecturally singular. Such an architecture singularity distance, which can be used by engineers as a criterion within the design process, is presented for a certain class of parallel manipulators of Stewart-Gough type; namely so-called linear pentapods. Geometrically the architecture singular designs are well-understood and can be subclassified into several cases, which allows to solve the optimization problem of computing the closest architecture singular design to a given linear pentapod with algorithms from numerical algebraic geometry.

Singularity Distance Computations of 3-RPR Manipulators Using Intrinsic Metrics

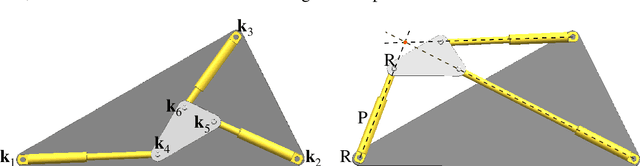
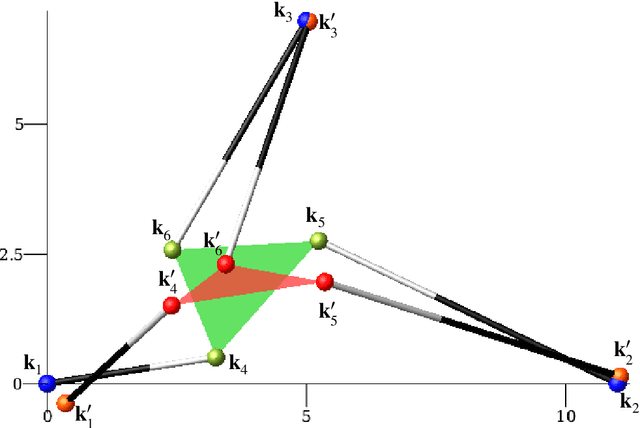
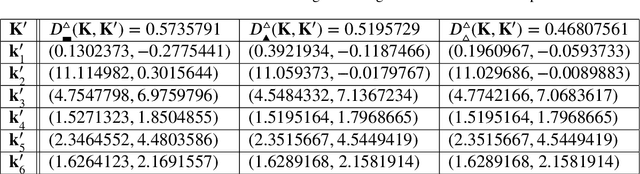
We present an efficient algorithm for computing the closest singular configuration to each non-singular pose of a 3-RPR planar manipulator performing a 1-parametric motion. By considering a 3-RPR manipulator as a planar framework, one can use methods from rigidity theory to compute the singularity distance with respect to an intrinsic metric. There are different design options as the platform/base can be seen as a triangular plate or as a pin-jointed triangular bar structure. Moreover, we also allow the additional possibility of pinning down the base/platform triangle to the fixed/moving system thus it cannot be deformed. For the resulting nine interpretations, we compute the corresponding intrinsic metrics based on the total elastic strain energy density of the framework using the physical concept of Green-Lagrange strain. The global optimization problem of finding the closest singular configuration with respect to these metrics is solved by using tools from numerical algebraic geometry. The proposed algorithm is demonstrated based on an example.

Singularity Distance Computations for 3-RPR Manipulators using Extrinsic Metrics

It is well-known that parallel manipulators are prone to singularities. There is still a lack of distance evaluation functions, referred to as metrics, for computing the distance between two 3-RPR configurations. The presented extrinsic metrics take the combinatorial structure of the manipulator into account as well as different design options. Using these extrinsic metrics, we formulate constrained optimization problems, which aim to find the closest singular configurations for a given non-singular configuration. The solution of the corresponding system of polynomial equations relies on algorithms from numerical algebraic geometry implemented in the software package Bertini. Moreover, we developed a computational pipeline for computing the singularity distance along a 1-parametric motion of the manipulator. To facilitate these computations for the user, an open-source interface is developed between software packages Maple, Bertini, and Paramotopy. The presented approach is demonstrated based on a numerical example.