Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
J. M. Selig
Mobile Icosapods
Mar 23, 2016Figures and Tables: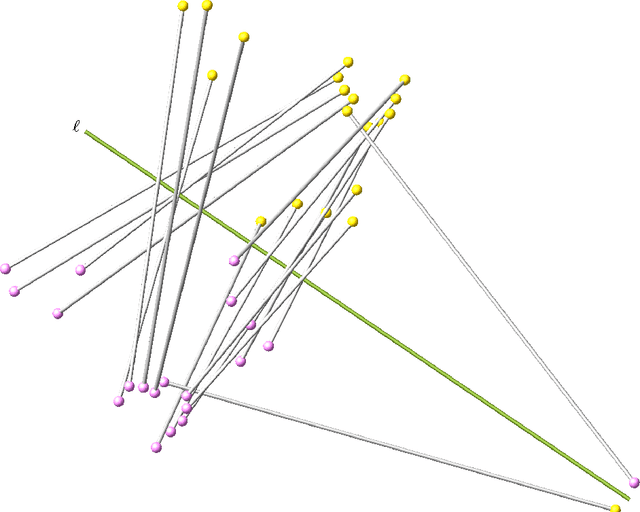
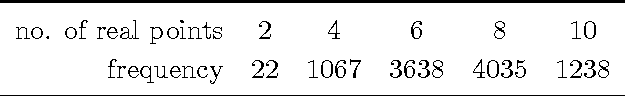



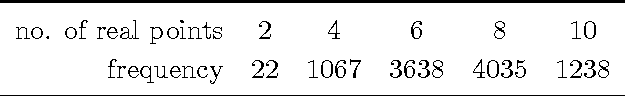


Abstract:Pods are mechanical devices constituted of two rigid bodies, the base and the platform, connected by a number of other rigid bodies, called legs, that are anchored via spherical joints. It is possible to prove that the maximal number of legs of a mobile pod, when finite, is 20. In 1904, Borel designed a technique to construct examples of such 20-pods, but could not constrain the legs to have base and platform points with real coordinates. We show that Borel's construction yields all mobile 20-pods, and that it is possible to construct examples with all real coordinates.
* Advances in Applied Mathematics, Volume 88, July 2017, Pages 1-25
* 22 pages, 4 figures
* 22 pages, 4 figures
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge