On the Classification of Motions of Paradoxically Movable Graphs
Paper and Code
Mar 25, 2020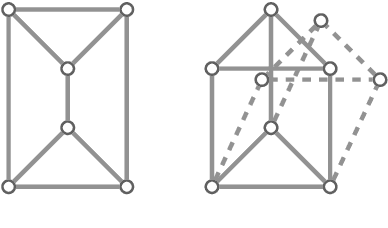
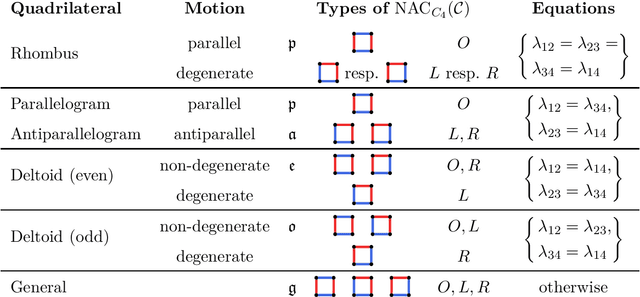
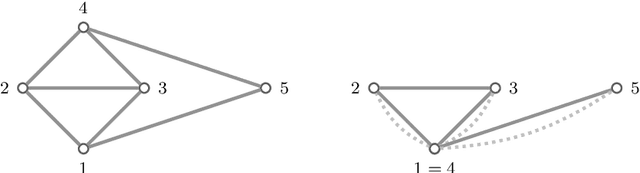
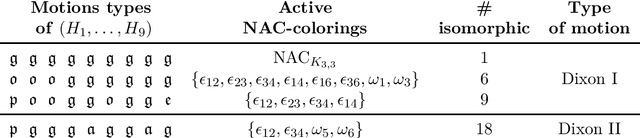
Edge lengths of a graph are called flexible if there exist infinitely many non-congruent realizations of the graph in the plane satisfying these edge lengths. It has been shown recently that a graph has flexible edge lengths if and only if the graph has a special type of edge coloring called NAC-coloring. We address the question how to determine all possible proper flexible edge lengths from the set of all NAC-colorings of a graph. We do so using restrictions to 4-cycle subgraphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge