Jan Legerský
FlexRiLoG -- A SageMath Package for Motions of Graphs
Mar 26, 2020
Abstract:In this paper we present the SageMath package FlexRiLoG (short for flexible and rigid labelings of graphs). Based on recent results the software generates motions of graphs using special edge colorings. The package computes and illustrates the colorings and the motions. We present the structure and usage of the package.
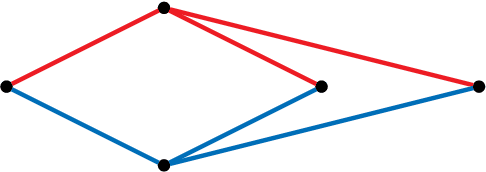
On the Classification of Motions of Paradoxically Movable Graphs
Mar 25, 2020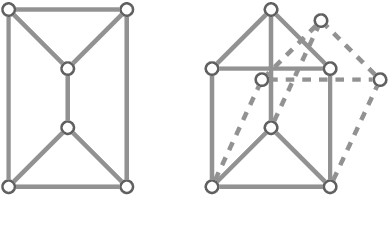
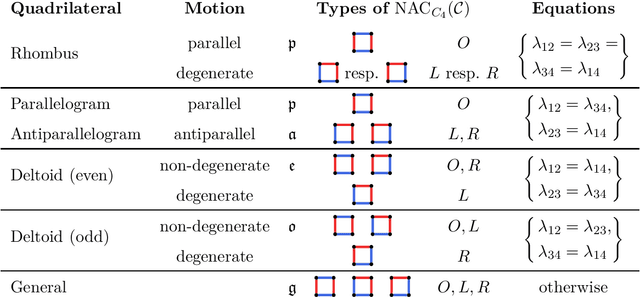
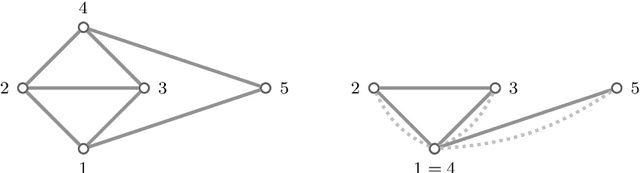
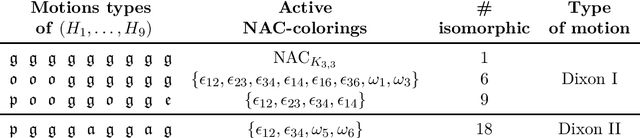
Abstract:Edge lengths of a graph are called flexible if there exist infinitely many non-congruent realizations of the graph in the plane satisfying these edge lengths. It has been shown recently that a graph has flexible edge lengths if and only if the graph has a special type of edge coloring called NAC-coloring. We address the question how to determine all possible proper flexible edge lengths from the set of all NAC-colorings of a graph. We do so using restrictions to 4-cycle subgraphs.
Flexible placements of graphs with rotational symmetry
Mar 20, 2020



Abstract:We study the existence of an $n$-fold rotationally symmetric placement of a symmetric graph in the plane allowing a continuous deformation that preserves the symmetry and the distances between adjacent vertices. We show that such a flexible placement exists if and only if the graph has a NAC-colouring satisfying an additional property on the symmetry; a NAC-colouring is a surjective edge colouring by two colours such that every cycle is either monochromatic, or there are at least two edges of each colour.
On the existence of paradoxical motions of generically rigid graphs on the sphere
Aug 01, 2019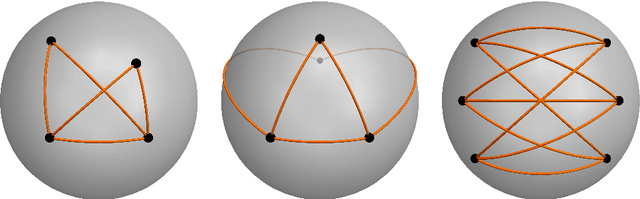
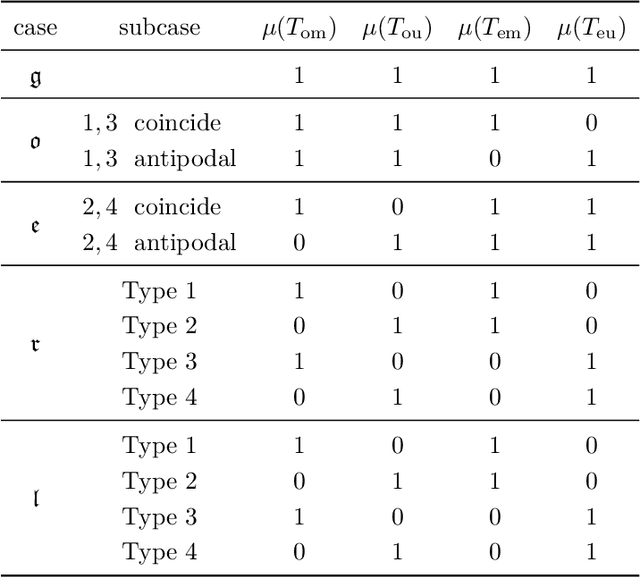

Abstract:We interpret realizations of a graph on the sphere up to rotations as elements of a moduli space of curves of genus zero. We focus on those graphs that admit an assignment of edge lengths on the sphere resulting in a flexible object. Our interpretation of realizations allows us to provide a combinatorial characterization of these graphs in terms of the existence of particular colorings of the edges. Moreover, we determine necessary relations for flexibility between the spherical lengths of the edges. We conclude by classifying all possible motions on the sphere of the complete bipartite graph with $3+3$ vertices where no two vertices coincide or are antipodal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge