From the Fundamental Theorem of Algebra to Kempe's Universality Theorem

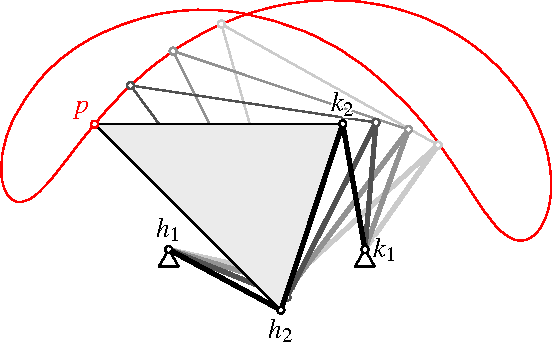
This article provides a gentle introduction for a general mathematical audience to the factorization theory of motion polynomials and its application in mechanism science. This theory connects in a rather unexpected way a seemingly abstract mathematical topic, the non-unique factorization of certain polynomials over the ring of dual quaternions, with engineering applications. Four years after its introduction, it is already clear how beneficial it has been to both fields.

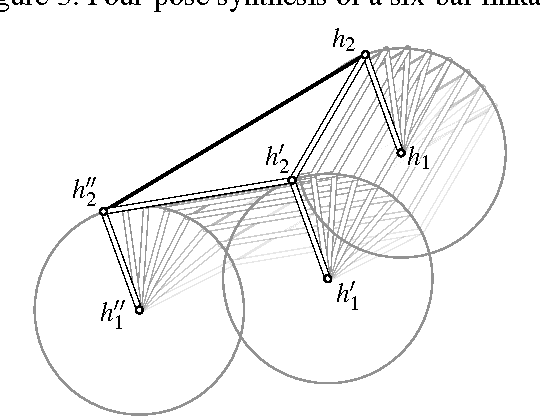
Four-Pose Synthesis of Angle-Symmetric 6R Linkages

We use the recently introduced factorization theory of motion polynomials over the dual quaternions for the synthesis of closed kinematic loops with six revolute joints that visit four prescribed poses. Our approach admits either no or a one-parametric family of solutions. We suggest strategies for picking good solutions from this family.

The Theory of Bonds: A New Method for the Analysis of Linkages

In this paper we introduce a new technique, based on dual quaternions, for the analysis of closed linkages with revolute joints: the theory of bonds. The bond structure comprises a lot of information on closed revolute chains with a one-parametric mobility. We demonstrate the usefulness of bond theory by giving a new and transparent proof for the well-known classification of overconstrained 5R linkages.

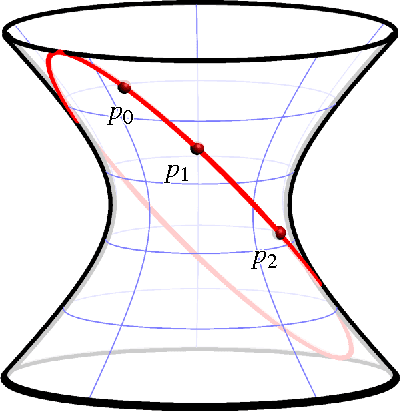
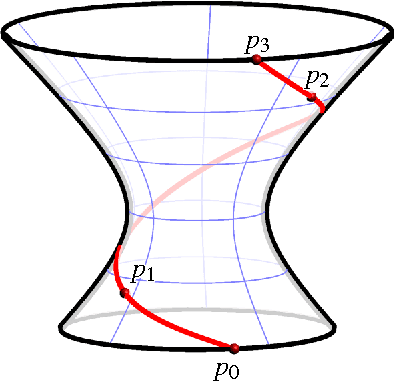
Factorization of Rational Curves in the Study Quadric and Revolute Linkages

Given a generic rational curve $C$ in the group of Euclidean displacements we construct a linkage such that the constrained motion of one of the links is exactly $C$. Our construction is based on the factorization of polynomials over dual quaternions. Low degree examples include the Bennett mechanisms and contain new types of overconstrained 6R-chains as sub-mechanisms.