Mechanism Singularities Revisited from an Algebraic Viewpoint

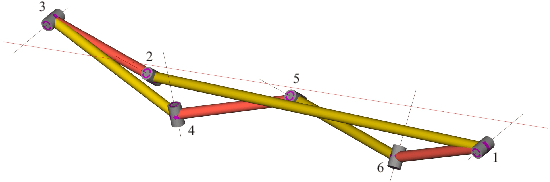
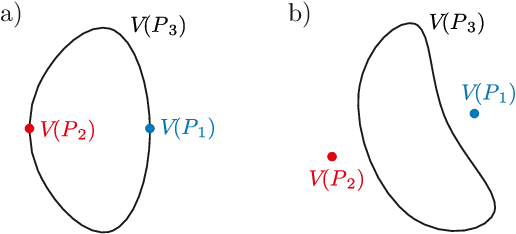
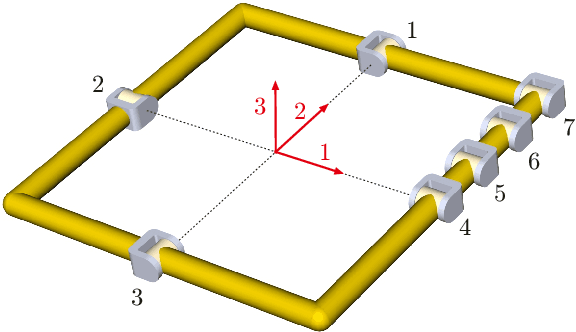
It has become obvious that certain singular phenomena cannot be explained by a mere investigation of the configuration space, defined as the solution set of the loop closure equations. For example, it was observed that a particular 6R linkage, constructed by a combination of two Goldberg 5R linkages, exhibits kinematic singularities at a smooth point in its configuration space. Such problems are addressed in this paper. To this end, an algebraic framework is used in which the constraints are formulated as polynomial equations using Study parameters. The algebraic object of study is the ideal generated by the constraint equations (the constraint ideal). Using basic tools from commutative algebra and algebraic geometry (primary decomposition, Hilbert's Nullstellensatz), the special phenomenon is related to the fact that the constraint ideal is not a radical ideal. With a primary decomposition of the constraint ideal, the associated prime ideal of one primary ideal contains strictly into the associated prime ideal of another primary ideal which also gives the smooth configuration curve. This analysis is extended to shaky and kinematotropic linkages, for which examples are presented.